Sprawdzanie założeń KMNK i poprawności modelu

1. Badanie współliniowości zmiennych objaśniających

Czynnik inflacji wariancji

- współczynnik determinacji w modelu, w którym zmienną objaśnianą jest x_j zaś zmiennymi objaśniającymi pozostałe k-1 zmiennych.

• brak współliniowości CIW_j=1

• współliniowość przybliżona CIW_j>10

2. Badanie losowości rozkładu składnika losowego

- liniowa postać modelu:

• test liczby serii

1. należy uporządkować niemalejąco reszty w próbie według zmiennej porządkującej; zmienną porządkującą jest zmienna czasowa dla danych z szeregów czasowych, lub jedna ze zmiennych objaśniających dla danych przekrojowych,

2. dla uporządkowanego ciągu obliczamy liczbę serii reszt modelu S,

3. z tablic testu serii dla liczby reszt dodatnich n₁, liczby reszt ujemnych n₂ oraz przyjętego poziomu istotności α/2 i 1-α/2 odczytujemy krytyczne liczby serii S₁^* i S₂^*,

4. jeśli S₁^*<S< S₂^* nie ma podstaw do odrzucenia H₀; gdy S< S₁^* lub S> S₂^* H₀ należy odrzucić,

5. test może także być stosowany do oceny poprawności doboru postaci analitycznej modelu innej niż liniowa; wówczas:

gdzie f jest dowolną funkcją.

• test normalny

Statystyka Z ma asymptotyczny rozkład normalny N(0,1).

3. Badanie homoskedastyczności składników losowych

Test Goldfelda-Guandta

1. porządkujemy niemalejąco obserwacje w próbie według zmiennej porządkującej. Dla danych z szeregów czasowych jest to najczęściej zmienna czasowa, dla danych przekrojowych zmienna podejrzewana o spowodowanie heteroskedastyczności,

2. wybieramy dwie skrajne podbróby (liczba pominiętych obserwacji nie powinna przekraczać 1/3 n); n₁- liczba obserwacji w pierwszej podpróbie, n₂- liczba obserwacji w drugiej podbróbie,

3. szacujemy parametry modelu osobno dla każdej podbróby i wyznaczamy wariancje resztowe:

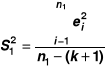
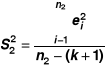
4. obliczamy:
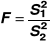
   ; w liczniku musi być większa z wariancji,

5. dla przyjętego poziomu istotności w tablicach wartości krytycznych rozkładu F odczytujemy wartość krytyczną F* dla liczby stopni swobody s₁=n₁-(k+1) oraz s₂=n₂-(k+1),

6. jeżeli F<F* nie ma podstaw do odrzucenia H₀; jeżeli F>F* odrzucamy H_0,

7. test znajduje zastosowanie w badaniu homoskedastyczności składnika losowego, gdy zróżnicowanie wariancji składnika losowego jest zależne od jednej tylko zmiennej.

4. Badanie autokorelacji pierwszego rzędu składnika losowego

Współczynnik autokorelacji z próby

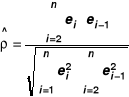
Test Durbina-Watsona

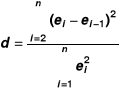
a) H₀: ρ=0 H₁: ρ>0

• d > d_u - nie ma podstaw do odrzucenia H₀,

• d < d_l - odrzucić H₀ (autokorelacja dodatnia),

• d_l < d < d_u - test nie daje rozstrzygnięcia

b) H₀: ρ=0 H₁: ρ<0

• d < 4 - d_u - nie ma podstaw do odrzucenia H₀,

• d > 4 - d_l - odrzucić H₀ (autokorelacja ujemna),

• 4 - d_u < d < 4 -d_l - test nie daje rozstrzygnięcia

c) H₀: ρ=0 H₁: ρ
0

• d_u < d < 4- d_u - nie ma podstaw do odrzucenia H₀,

• 0 < d < d_l lub 4 - d_l < d < 4 - odrzucamy H₀,

• 4 - d_u < d < 4- d_l lub d_l < d < d_u - obszar niekonkluzywności testu.

W przypadku braku rozstrzygnięcia kwestii istnienia autokorelacji pierwszego rzędu testem Durbina-Watsona stosujemy:

test mnożnika Lagrange'a

H₀: ρ=0 H₁: ρ
0

• wyznaczamy reszty w modelu pierwotnym,

• szacujemy model pomocniczy:

dla i=2,3,...,n,

• wyznaczamy dla tego modelu R² i obliczamy wartość wyrażenia (n-1)R² i porównujemy ją z wartością krytyczną chi-kwadrat dla poziomu istotności α i liczby stopni swobody s=1, oznaczoną χ²_*.

• jeżeli (n-1)R²>χ²_* to odrzucamy hipotezę zerową (wystąpiła autokorelacja); dla (n-1)R²<χ²_* nie ma podstaw do odrzucenia hipotezy zerowej o braku autokorelacji pierwszego rzędu.

• warunkiem stosowania testu jest duża liczba obserwacji.

5. Badanie normalności rozkładu składnika losowego

H₀: składnik losowy modelu Y=Xβ+ε ma rozkład normalny

H₁: składnik losowy modelu Y=Xβ+ε nie ma rozkładu normalnego

Test Jarque-Bera

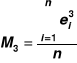
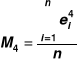
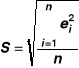
• JBT ma asymptotyczny rozkład chi-kwadrat z liczbą stopni swobody s=2, oznaczoną χ²_*,

• jeżeli JBT>χ²_* hipotezę zerową należy odrzucić; dla JBT<χ²_* nie ma podstaw do odrzucenia hipotezy zerowej,

• test JBT może być stosowany wyłącznie dla dużych prób.

41

---