Nr i tytuł ćwiczenia: Ćwiczenie 1-1. Wyznaczanie ciepła rozpuszczania
Imię i nazwisko osoby prowadzącej ćwiczenia: Bożena Parczewska Plesnar
Data wykonania ćwiczenia	Godz.	Nr grupy studenckiej	Zespół	Nazwiska osób wykonujących ćw.	Pkt za spr
14.04.2010	11-14	1	c	Marta Brzostowska Katarzyna Szkop
Uwagi prowadzącego:

1.Cel ćwiczenia

Celem ćwiczenia jest wyznaczanie ciepła rozpuszczania substancji stałych (kwasu benzoesowego) oraz pomiarów ich rozpuszczalności w różnych temperaturach.

2.Wstęp teoretyczny:

Ciepło rozpuszczania- efekt energetyczny towarzyszący procesowi rozpuszczania. Rozpuszczanie różni się od reakcji chemicznej tym, że w odróżnieniu do reakcji chemicznej ilość substancji biorących udział w procesie rozpuszczania nie musi spełniać ściśle określonych stosunków masowych. Efekt energetyczny towarzyszący procesowi rozpuszczania zależy od: rodzaju substancji rozpuszczanej i rozpuszczalnika, od tego ,czy dana substancja jest wprowadzana do czystego roztworu lub do roztworu o określonym stężeniu oraz od wartości początkowego i końcowego stężenia roztworu. Rozróżnia się kilka rodzajów ciepła rozpuszczania: molowe ciepło rozpuszczania, pierwsze ciepło rozpuszczania, pełne ciepło rozpuszczania, pełne ciepło rozpuszczania, cząstkowe ciepło rozpuszczania, ostatnie ciepło rozpuszczania.

Wartość ciepła rozpuszczania pod stałym ciśnieniem (entalpię rozpuszczania ΔH_r) można wyznaczyć w bezpośrednich pomiarach kalorymetrycznych lub obliczyć z równania izobary van't Hoffa na podstawie danych o rozpuszczalności substancji w danym rozpuszczalniku w różnych temperaturach.

Rozpuszczalność (R_s) to stosunek masy substancji rozpuszczonej do masy rozpuszczalnika:

R_s=m_s/m_r

Gdzie:

m_s - masa substancji rozpuszczonej

m_r - masa rozpuszczalnika

Najczęściej podawana jest rozpuszczalność substancji w 100g rozpuszczalnika, a więc obliczana z zależności:

R_s=(m_s/m_r)100

Eksperymentalnie rozpuszczalność wyznacza się, wprowadzając do rozpuszczalnika nadmiar substancji rozpuszczanej i wytrząsając lub mieszając roztwór w stałej temperaturze doprowadza się do stanu równowagi. Następnie po odsączeniu osadu określa się jedną z metod analitycznych stężenie substancji w roztworze nasyconym.

Oblicza się stałą równowagi (K) procesu:

(AB)_S↔(AB)_C

Gdzie:

(AB)_S - substancja rozpuszczana występująca w fazie stałej

(AB)_C - substancja rozpuszczana występująca w roztworze nasyconym,

Z zależności:

K=[AB]_C/[AB]_S

Ponieważ w wyrażeniu tym wielkość [AB]_S ma stałą wartość, zależną jedynie od powierzchni fazy stałej, która praktycznie jest stała, więc stałą równowagi (K) oblicza się z równania:

K=[AB]_C

Gdzie [AB]_C = R_s , tzn. jest równa rozpuszczalności badanej substancji.

Wpływ temperatury na tę równowagę opisuje równanie izobary van't Hoffa:

d(lnK)/dT= ΔH/RT²

gdzie:

K - stała równowagi, równa rozpuszczalności (R_s) w temperaturze T

ΔH - entalpia rozpuszczania, czyli efekt energetyczny związany z procesem rozpuszczania substancji w danej temperaturze i pod stałym ciśnieniem (prowadzący do otrzymania roztworu nasyconego).

Całkując równanie d(lnK)/dT= ΔH/RT² w przedziale temperatur T₁-T₂ - przy założeniu, że ΔH nie zmienia się w tym zakresie temperatury, otrzymuje się wyrażenie na entalpię rozpuszczania:

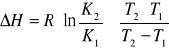
Gdzie:

K₂ i K₁ - rozpuszczalność substancji odpowiednio w temperaturze T₂ i T₁

R - stała gazowa (8,313 J∙mol^-1∙K^-1 ).

3. Wykonanie ćwiczenia

Na wadze technicznej odważamy mniej więcej po 2 g kwasu benzoesowego i wsypujemy go do 4 ponumerowanych kolb stożkowych z korkiem na szlif o pojemności 100 cm³. Do każdej kolby dodajemy po 80 cm³ wody destylowanej odmierzonej cylindrem, podgrzanej do temperatury około 60°C. Dwie kolby wkładamy do wytrząsarki na około 30 minut, a pozostałe dwie wytrząsamy chwile i wkładamy do łaźni parowej o temperaturze 40°C. Ważymy na wadze technicznej 4 puste kolby stożkowe o pojemności 250 cm³. Następnie bez wyjmowania kolb z termostatów pobiera się kolejno, pipetą o objętości 25 cm³ (z nasuniętym na jej koniec wężykiem gumowym, zawierającym zatyczkę z waty w charakterze sączka) i 50 cm³ z kolb wytrząsanych na wytrząsarce, nasycony roztwór badanej substancji. Pobrane roztwory przenosi się do zważonych kolb stożkowych. Kolby z roztworami ważymy na wadze. Przeprowadzamy miareczkowanie mianowanym roztworem NaOH w obecności fenoloftaleiny.

4.Opracowanie wyników

1. obliczenie Δm

Nr. kolby	Masa pustej kolby stożkowej[g]	Masa kolby z roztworem [g]	Δm [g]
1	133.47	183.25	49,78
2	128.98	178.74	49,76
3	108.08	132.87	24,79
4	127.85	152.63	24,78

2. obliczanie gęstości roztworów ze wzoru
   ,

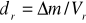
gdzie: Δm - różnica mas kolby z nasyconym roztworem kwasu benzoesowego i kolby pustej, V_r - objętość kwasu przed miareczkowaniem

Obliczenia dla roztworów:

Nr. kolby	Δm [g]	Vr [cm^3]	dr [g/cm^3]
1	49,78	50	0,9956
2	49,76	50	0,9952
3	24,79	25	0,9916
4	24,78	25	0,9912

3. obliczanie stężenia molowego kwasu benzoesowego z zależności:

gdzie V_kwasu - objętość roztworu przed miareczkowaniem, c_kwasu - stężenie molowe kwasu benzoesowego w roztworze, V_NaOH - objętość mianowanego roztworu NaOH użyta podczas miareczkowania, c_NaOH - stężenie mianowanego roztworu NaOH (0,1003 mol/dm³)

Nr. kolby	VNaOH [cm^3]	cNaOH [mol/dm^3]	Vkwasu [cm^3]	ckwasu [mol/dm^3]
1	20.00	0,1003	50	0,04012
2	23.00	0,1003	50	0,04614
3	13.00	0,1003	25	0,05216
4	13.70	0,1003	25	0,05496

• Kolba numer 1 - c_kwasu=0,1003mol∙dm^-3∙20cm³/50cm³=0,04012 mol∙dm^-3

• Kolba numer 2 - c_kwasu=0,1003mol∙dm^-3∙23cm³/50cm³=0,04614 mol∙dm^-3

• Kolba numer 3 - c_kwasu=0,1003mol∙dm^-3∙13cm³/25cm³=0,05216 mol∙dm^-3

• Kolba numer 4 - c_kwasu=0,1003mol∙dm^-3∙13.7cm³/25cm³=0,05496 mol∙dm^-3

d) obliczenie rozpuszczalności z zależności:

K=

gdzie: c_r - stężenie molowe wyznaczone metodą miareczkowania alkacymetrycznego roztworu nasyconego w danej temperaturze [mol/dm³], M_s - masa molowa substancji (dla kwasu benzoesowego = 122,12 g/mol), d_r - gęstość roztworu nasyconego danej substancji [g/dm³].

Nr. kolby	cr [mol/dm^3]	dr [g/dm^3]	Rs [g/100 cm^3 H2O]
1	0,04012	995,6	0,4921
2	0,04614	995,2	0,5662
3	0,05216	991,6	0,6424
4	0,05496	991,2	0,6771

• Kolba numer 1-R_s=(0,04012mol∙dm^-3∙122,12g∙mol^-1/995,6 g∙dm^-3)∙100 =0,4921g/100 g H₂O

• Kolba numer 2-R_s=(0,04614mol∙dm^-3∙122,12g∙mol^-1/995,2g∙dm^-3)∙100 =0,5662g/100 g H₂O

• Kolba numer 3-R_s=(0,05216mol∙dm^-3∙122,12g∙mol^-1/991,6g∙dm^-3)∙100 =0,6424g/100 g H₂O

• Kolba numer 4-R_s=(0,05496mol∙dm^-3∙122,12g∙mol^-1/991,2g∙dm^-3)∙100 =0,6771g/100 g H₂O

e) wyznaczenie entalpii procesu rozpuszczania,

T₁ K₁ = (R₁+R₂)/2=(0,4921g+0,5662g)/2=0,5292g/100g H₂O

K
=(R₃+R₄)/2=(0,6424g+0,6771g)/2=0,6597g/100g H₂O

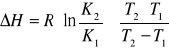
gdzie: K₂ i K₁ - rozpuszczalność substancji w temperaturach T₂ i T₁, R - stała gazowa [
], T₁ - 296,0 K, T₂ - 313,0K. Podstawiając dane do wzoru otrzymujemy:

∆H=8,313J∙mol^-1∙K^-1(ln 0,6597/0,5292)∙[313,0 K∙296,0 K/(313,0K−296,0K)]=9986,04 J∙mol^-1

Wartość średnia ΔH wynosi 9986,04 J/mol≈10 kJ/mol

Wyznaczanie entalpii rozpuszczania biorąc pod uwagę kąt nachylenia prostej:

A=(0,003167; -0,451) B=(0,00341; -0,978)

a=(y₂-y₁)/(x₂-x₁)=[-0,978+(-0,451)]/( 0,00341-0,003167)= -0,527/0,000243= -2168,72K

a=-ΔH/R

ΔH=-aR= -2168,72K ∙ 8,313J/mol∙K=18028,60 J/mol

5.Wnioski

Zapoznałyśmy się z metodą wyznaczania ciepła rozpuszczania substancji w stanie stałym z pomiarów jej rozpuszczalności w różnych temperaturach.

Z przebiegu obrazu graficznego wnioskujemy, że proces jest reakcją endotermiczną.

Rozpuszczalność danej reakcji wzrasta wraz ze wzrostem temperatury.

Wyniki uzyskane metodą teoretyczną 18388,99J/mol oraz algebraiczną 18028,60 J/mol są bardzo zbliżone.

Wszelkie wartości, które odbiegają od siebie na wykresie mogą być spowodowane błędami pomiarowymi, błędami podczas miareczkowania, ochłodzeniem się roztworu, wytrąceniem części kwasu.

---