Zad. 1.

Niech B będzie drużyną, która wygrała najwięcej meczów (może oczywiście być więcej drużyn, które wygrały tak samo dużo meczów, co B). Niech X oznacza zbiór drużyn, z którymi wygrała B. Niech A będzie dowolną drużyną, która wygrała z B (z założeń wynika, że jest co najmniej jedna taka drużyna). Gdyby A wygrała ze wszystkimi drużynami ze zbioru X, to wygrałaby więcej meczów niż B, a zatem istnieje drużyna C ∈ X, która wygrała z A, cnd.

Zad. 2.

(a) 1, 9, 10

(b) 5, 6, 7, 8, 9, 10

(c) 2

(d) 1, 2, 3, 4, 5

Zad. 3.

(a)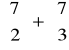

(b) 3!⋅2³

(c)

(d) 1⋅2 + 1⋅3 + 1⋅4 + 2⋅3 + 2⋅4 + 3⋅4

Zad. 4.

	K2 + N4	K2 + P3	K1,1,2,2
χ(G)	3	4	4
χ'(G)	5	5	5
rad(G)	1	1	1
τ(G)	1	1	2
chl(G)	10	11	14
ω(G)	3	4	4
cir(G)	4	5	6

Zad. 5

6

5

1

2

3

4

Zad. 6

Rozwinięcie:

Sprawdzenie przez indukcję:

---