Egzamin z matematyki dyskretnej 21 czerwiec 2006

Imię:

Nazwisko:

Grupa:

Numer Indeksu:

Uwagi:

1. Czas rozwiązywania 90 minut.

2. Ewentualne wątpliwości związane z niejednoznacznością sformułowań w zadaniach należy umieścić obok udzielonych odpowiedzi.

3. Dozwolone jest korzystanie z pomocy w formie własnoręcznych notatek i wydruków slajdów z wykładu. Nie wolno korzystać z książek i urządzeń elektronicznych.

4. Zbiór liczb naturalnych nie zawiera zera: 0 ∉ N.

5. Zapis "a | b" oznacza "a jest dzielnikiem b" czyli "b jest podzielne przez a".

6. W trakcie egzaminu nie wolno opuszczać sali przed oddaniem pracy.

7. Skala ocen jest opisana notacją (a/b/c) gdzie a - liczba pkt. za poprawną odp., b - liczba pkt. za brak odp., c - liczba pkt. za błędną odp.

8. Za żadne z siedmiu zadań nie można uzyskać mniej niż 0 pkt.

9. Rozwiązania zadań 1 oraz 2(a)oraz 3(a) należy umieścić na odwrocie.

Zad. 1. (10 pkt. 10/0/0) Dany jest ciąg określony rekurencyjnie:

Udowodnij, że
dla każdej liczby naturalnej n ∈ N.

Zad. 2. (10 pkt. 2/0/0) Dana jest relacja określona w zbiorze liczb naturalnych formułą xRy ⇔ ∃_p∈N xy = p².

(a) Udowodnij, że R jest relacją typu równoważności.

(b) Ile klas abstrakcji ma ta relacja? _{................................ ................................ ................................ ................................}

(c) Wyznacz [6]_R ∩ {1,2,...,100} = _{................................ ................................ ................................ ................................}

(d) Wyznacz min [2³·3⁴·4⁵·5⁶]_R = _{................................ ................................ ................................ ................................}

(e) Wyznacz min [3²·4³·5⁴·6⁵]_R =_{................................................................................................................................}

Zad. 3. (10 pkt. 2/0/0) Dany jest zbiór ciągów binarnych A = {0, 1, 01, 10, 11, 010, 100, 111, 0111}. Definiujemy relację porządku częściowego R ⊆ A² w ten sposób, że aRb wtedy i tylko wtedy gdy ciąg b zawiera podciąg a. Czyli np. 001R0101 ale nieprawda, że 110R0101).

(a) Narysuj diagram Hasse'go tego porządku.

Wyznacz:

(b) wszystkie elementy maksymalne w A względem R_{................................}

(c) wszystkie elementy minimalne w A względem R_{................................}

(d) najdłuższy łańcuch w A względem R_{................................}

(e) najdłuższy antyłańcuch w A względem R_{................................}

Zad. 4. (10 pkt. 5/0/0) Danych jest 10 piłek: 3 białe, 2 żółte oraz 5 zielonych oraz trzy koszyki biały, żółty i zielony. Na ile sposobów można umieścić piłki w koszykach tak, aby żadna piłka nie znalazła się w koszyku o tym samym kolorze co ona sama?

(a) Przyjmujemy, że piłki w tym samym kolorze są nierozróżnialne_{..................................................................}

(b) Przyjmujemy, że piłki są ponumerowane od 1 do 10_{............................................................. ................................}

Zad. 5. (10 pkt. 0.25/0/-0.25) Wyznacz wybrane parametry następujących grafów:

	K3,3	K3,3 - e	K2,2,2
χ(G)
χ'(G)
rad(G)
ၳ(G)
chl(G)
ω(G)
cir(G)
obw(G)

Zad. 6 (10 pkt.) Uporządkuj według niemalejącego tępa wzrostu następujące funkcje (tak, że jeśli f występuje przed g, to zachodzi f = O(g)):

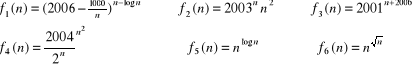
Zad. 7 (10 pkt. 10/0/0) Wyznacz wszystkie rozwiązania poniższego układu kongruencji dla 0 ≤ x ≤ 200.

x ≡ 3 mod 4

x ≡ 2 mod 5

x ≡ 3 mod 6

Przestroga. Zauważ, że NWD(4, 6) ≠ 1.

Pierwiastki powyższego układu kongruencji:_{.................................................................}

Długość marszruty chińskiego listonosza

Długość najdłuższego cyklu

Długość najkrótszego cyklu

---