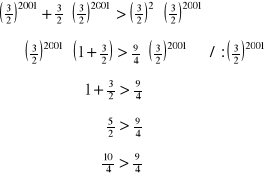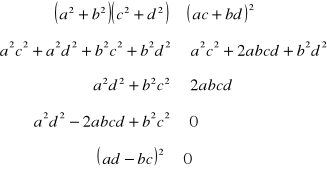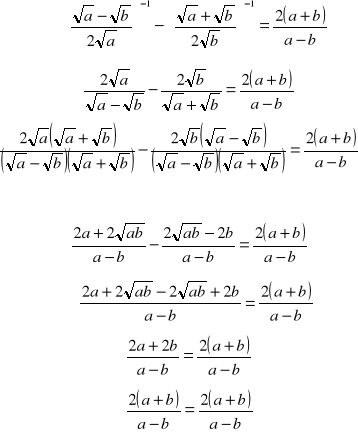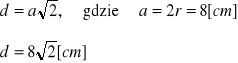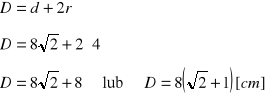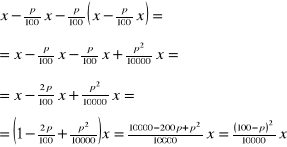KLUCZ

IV Wojewódzki Konkurs Matematyczny dla uczniów gimnazjum

eliminacje szkolne 2003/2004

• Uczeń ma wybrać i rozwiązać pięć spośród sześciu zadań.

• Uczeń może maksymalnie uzyskać 40 punktów.

• Wszystkie zadania są tak samo punktowane ( po 8 punktów ).

• Do etapu rejonowego kwalifikuje zdobycie co najmniej 38 punktów, co stanowi 95% punktów możliwych do uzyskania za poprawne rozwiązanie pięciu zadań.

Nr zad.	Rozwiązanie	Punktacja
1.	Podanie warunku konstrukcji trójkąta słownie lub w postaci nierówności: Przekształcenie nierówności do najprostszej postaci: Odp. Otrzymaliśmy nierówność prawdziwą, więc z podanych odcinków można zbudować trójkąt.	2p. 1p. 2p. 1p. 1p. 1p. łącznie 8p.
2.	Uzasadnienie: Nierówność jest prawdziwa dla dowolnych a, b, c, d ∈ R, gdyż kwadrat każdej liczby rzeczywistej jest liczbą nieujemną.	2p. ( za przekształcenie każdej ze stron po 1p.) 1p. 1p. 1p. 3p. łącznie 8p.

Nr zad.	Rozwiązanie	Punktacja
3.	Odp. Nierówność jest prawdziwa. ( lub zapis L=P )	1p. 2p. ( za każdy ułamek po 1p.) 2p. ( za każdy ułamek po 1p.) 1p. 1p. 1p. łącznie 8p.
4.	Rysunek kwadratu w układzie współrzędnych. Wyznaczenie współrzędnych punktów A = ( -2, -2 ) C = ( 2, 2 ). ( punkty A i C mogą być nazwane odwrotnie ) Rozpatrywanie dwóch przypadków - funkcja przechodzi przez punkt A lub C ( gdyż jest funkcją malejącą ). 1). A = ( -2, -2 ) Odp. Funkcja ma dokładnie jeden punkt wspólny z kwadratem dla b = 6 lub b = - 6.	1p. 1p. 1p. 2p. ( za każde równanie po 1p.) 2p. ( za każdy przykład po 1p.) 1p. łącznie 8p.

Nr zad.	Rozwiązanie	Punktacja
5.	Wykonanie rysunku z oznaczeniami i wypisanie danych. r = 4 cm, a - bok kwadratu, d - przekątna kwadratu, D - średnica garnka. Obliczenie przekątnej kwadratu: Obliczenie średnicy garnka: Odp. Średnica garnka musi mieć co najmniej	2p. 2p. ( przekątną można też obliczyć z twierdzenia Pitagorasa ) 2p. 1p. 1p. łącznie 8p.
6.	Wypisanie danych: x - początkowa cena towaru, p % - procent obniżki ceny. Cena towaru po pierwszej obniżce: x - p % x Cena towaru po drugiej obniżce ( cena końcowa ): x - p % x - p % ( x - p % x ) Uproszczenie wyrażenia opisującego końcową cenę towaru:	1p. 1p. 2p. 1p. 1p. 1p. 1p. łącznie 8p.

1

Hanna Kozłowska, Katarzyna Matuszek, Antonina Wiącek

Gimnazjum nr 27 z Oddziałami Integracyjnymi w Poznaniu

2). C = ( 2, 2 )

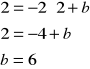
R

r

---