ĆWICZENIE NR 15
TEMAT: Wyznaczanie współczynnika lepkości metodą Stokesa
1. Opis teoretyczny
Jeżeli w dwóch stykających się ze sobą warstwach płynów rzeczywistych prędkości przepływającego płynu są różne, to obserwujemy stan przejściowy, podczas którego zachodzą procesy dążące do wyrównania prędkości w obu warstwach. Procesy te noszą nazwę tarcia wewnętrznego lub lepkości i mierzone są ilościowo współczynnikiem lepkości.
Wskutek tarcia występującego między cząsteczkami cieczy lub gazu cząsteczka która się nie porusza pociąga za sobą cząsteczki sąsiadujące z prędkością zbliżoną do własnej prędkości (prędkość ta będzie bardziej zbliżona jeżeli dana ciecz lub gaz będzie bardziej lepka). Zaś jeśli cząsteczka będzie spoczywać to będzie hamować sąsiednie cząsteczki.
Rozważać będziemy ciało stałe (kulkę metalową) poruszającą się w ośrodku ciekłym (olej) która będzie napotykać na opór. W otoczeniu cieczy obserwujemy wtedy ruch cieczy. Mechanizm tego zjawiska jest następujący:
Ciecz zwilżająca pokrywa cienką warstwą ciała w niej zanurzone. Z tego powodu gdy kulka jest w ruchu unosi ze sobą warstwę przylegającego płynu a ten na skutek zjawiska tarcia wewnątrz samego płynu wprawia w ruch następne warstwy. Z omawianych powyżej powodów siła z jaką płyn działa na poruszającą się kulkę zależy od współczynnika lepkości płynu i wyraża się wzorem:
Fl = -Kl v
Gdzie K to stała zależna od kształtu ciała . Dla kuli mamy K = 6 i dane równanie przybiera postać równania Stokesa które zapisujemy następująco:
Fl = 6 r v
Zgodnie z prawem Stokesa wraz z wzrastaniem prędkości wzrasta opór lepkości i w pewnej chwili siła ciężkości staje się równa sumie Fl + Fw
Fw=Vρcg
gdzie: ρc -gęstość cieczy (ośrodka)
Warunek równowagi sił ma postać:
mg = 6πrn + Vρcg
skąd:
![]()
Powyższe równanie jest słuszne jedynie w zastosowaniu do cieczy nieskończenie rozciągłych tzn. znajdujących się w bardzo szerokich naczyniach. Jeżeli kulka spada w rurze cylindrycznej o promieniu R, występujące wówczas pływy zmniejszają prędkość spadania i do powyższego wzoru należy wprowadzić czynnik korekcyjny zależny od stosunku r/R. Otrzymujemy wówczas skorygowany wzór:
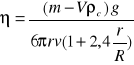
2. Metoda pomiaru wiskozymetrem Stokesa.
Aparatura składa się z cylindra szklanego o wysokości 0,693mm wypełnionego cieczą (olejem). Kulki powinny spadać mniej więcej wzdłuż osi cylindra w tym celu użyliśmy lejka.
III. Wyprowadzenie wzorów roboczych.
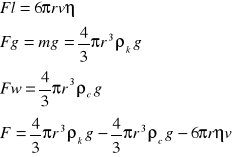
Zakładając, że F=0 oraz v=l/t gdzie t - czas spadania kulki na drodze l, otrzymamy:
IV. Opis przeprowadzonego eksperymentu
Do przeprowadzenia eksperymentu użyłem dziesięciu ołowianych kulek których średnice zmierzyłem za pomocą śruby mikrometrycznej. W dalszej kolejności zmierzyłem długość l którą pokonywała kulka za pomocą miarki milimetrowej. Następnie mierzyłem czas który pokonywała kulka (od górnego pierścienia do dolnego pierścienia) za pomocą sekundomierza. Czynność tą powtarzałem dziesięć razy i po każdych pomiarach zapisywałem do notatnika. Na końcu wyznaczyłem współczynniki lepkości dla każdej kulki korzystając ze wcześniej wyprowadzonego wzoru. Następnie korzystając ze wzoru na średnią arytmetyczną wyznaczyłem średni współczynnik lepkości badanej cieczy.
Wnioski
Ewentualnie występujący znaczący błąd pomiaru mógł wystąpić przez małą dokładność wzorcowania stopera, na którą składa się również refleks operatora. Można by przeprowadzić bardzo dokładny pomiar, gdyby układ pomiaru czas spadku kulki był cyfrowy, a tuba byłaby o wiele wyższa, co skutkowałoby dłuższym czasem spadku oraz prędkością bardziej zbliżoną do jednostajnej.
Składowych błędu nie widać w obliczeniach, jednak można go zauważyć w wynikach pomiaru.
Ćwiczenie nr 32
Temat: Pomiar stałej siatki dyfrakcyjnej za pomocą światła laserowego.
PODSTAWY TEORETYCZNE
1. Falowy charakter światła.
Światło jest falą elektromagnetyczną rozchodzącą się w próżni ze stałą prędkością c.
Jest rozchodzącym się w przestrzeni zaburzeniem pola elektromagnetycznego.
Do celów optycznych potrzebne jest jedynie opisanie w czasie wektora elektrycznego fali świetlnej równaniem (dla fali biegnącej w kierunku osi x):
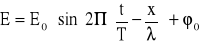
2. Zasada Hyghensa.
Jest ona oparta na konstrukcji geometrycznej i nie daje tak pełnego obrazu jak elektromagnetyczna teoria Maxwella. Brzmi ona: każdy punkt, który fala napotyka na swojej drodze staje się źródłem nowej fali kulistej; położenie fali można odczytać jako styczną do fal cząstkowych. Jest to podstawa wyjaśnienia zjawisk dyfrakcji i interferencji.
3. Interferencja.
Jest to wzajemne nakładanie się fal. W określonym punkcie przestrzeni nastąpi wzmocnienie lub wygaszenie amplitudy w zależności od faz fal w tym punkcie.
a) Warunkiem na wygaszenie się wzajemne dwóch fal jest odwrotność ich faz, czyli różnica odległości od źródeł musi być równa połowie wielokrotności długości fali.
b) Warunek zaś konieczny do wygaszenia się dwóch fal to zgodność ich faz, czyli różnica odległości od źródeł musi być równa całkowitej wielokrotności długości fali.
Chociaż interferencja zachodzi dla dowolnych fal to stały w czasie obraz interferencyjny można zaobserwować jedynie dla źródeł spójnych (o stałej w czasie różnicy faz).
4. Dyfrakcja.
Jest to zjawisko ugięcia się fali zauważalne, gdy przechodzi ona przez szczelinę o rozmiarach porównywalnych z długością fali.
OPIS DOŚWIADCZENIA
Spójna ( koherentna ) wiązka światła przechodząc przez dwie jednakowe szczeliny ulega na nich ugięciu, dając po przejściu przez szczelinę dwie fale spójne interferujące ze sobą. W wyniku interferencji otrzymuje się na ekranie umieszczonym w pewnej odległości za szczelinami jasne i ciemne prążki interferencyjne.
Ćwiczenie, wykorzystuje opisane zjawisko z tą różnicą, że zamiast dwóch znajduje się znacznie więcej jednakowych, równoległych szczelin, których liczba może dochodzić do kilkunastu tysięcy. Tworzą one tak zwaną siatkę dyfrakcyjną.
Fala świetlna po przejściu przez szczeliny interferuje tworząc na ekranie maksima interferencyjne widoczne w postaci prążków ( przede wszystkim I - go rzędu ).
Stałą siatki d ( odległość między środkami każdej pary dwóch sąsiednich szczelin ) obliczamy następująco:
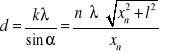
WYPROWADZENIE WZORU ROBOCZEGO
![]()
![]()
- równanie opisujące położenie kolejnych minimów dyfrakcyjnych
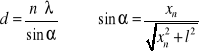
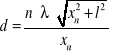
WNIOSKI
- Wyliczona wartość stałej siatki dyfrakcyjnej może odbiegać w znaczny sposób od rzeczywistej wartości, z powodu złego stanu technicznego siatki.
- Wpływ na błąd pomiaru może mieć słaba widoczność maksimów interferencyjnych
- Układ pomiarowy wykorzystany w doświadczeniu może posłużyć nam także do wyznaczenia długości fali nieznanego źródła światła pod warunkiem, że będziemy znali stałą siatki dyfrakcyjnej.
1
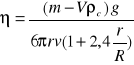
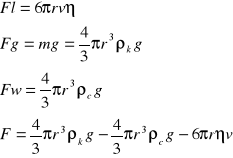
Fl
Fw
Fg
![]()
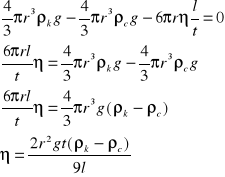
Wyszukiwarka
Podobne podstrony:
Promieniowanie ćw.30, Transport UTP, semestr 1, ffiza, laborki różne, Laborki, Laborki, Fizyka - mat
sprawozdanie3, Transport UTP, semestr 1, ffiza, laborki różne, Laborki, Laborki, Fizyka - materiały
lab4, Transport UTP, semestr 1, ffiza, laborki różne, Laborki, Laborki, Fizyka - materiały na labora
kolos, Transport UTP, semestr 1, ffiza, laborki różne, Laborki, Laborki, Fizyka - materiały na labor
Wiązania krystaliczne, Transport UTP, semestr 1, ffiza, laborki różne, Laborki, Laborki, Fizyka - ma
Wyklad34, Transport UTP, semestr 1, ffiza, laborki różne, Laborki, Laborki, Fizyka - materiały na la
Cwiczenie 30, Transport UTP, semestr 1, ffiza, laborki różne, Laborki, Laborki, fizyka laborki, labo
wyklad16, Transport UTP, semestr 1, ffiza, laborki różne, Laborki, Laborki, Fizyka - materiały na la
WIEiK-cwiczenia(2), Transport UTP, semestr 1, ffiza, laborki różne, Laborki, Laborki, Fizyka - mater
Wyznaczanie mod. szczywności G, Transport UTP, semestr 1, ffiza, laborki różne, Laborki, Laborki, Fi
wykresy, Transport UTP, semestr 1, ffiza, laborki różne, Laborki, Laborki, Fizyka - materiały na lab
cw11.2, Transport UTP, semestr 1, ffiza, laborki różne, Laborki, Laborki, Fizyka - materiały na labo
więcej podobnych podstron