PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA INSTYTUT POLITECHNICZNY
2003/2004	LABORATORIUM Z FIZYKI
Ćwiczenie nr 4	BADANIE PRAWA STEFANA - BOLTZMANA
Budowa i Eksploatacja Maszyn ST. Zaoczne Semestr II	Dyksik Arnold Stefaniak Łukasz Kania Mateusz
Data wykonania		Data	Ocena	Podpis
2004-03-12	T
	S

1. Problemy do rozwiązania:

1.Pomiar oporu rozżarzonego włókna żarówki w temperaturze pokojowej i określenie oporu Ro włókna w temperaturze zero stopni.

2.Pomiar strumienia energii emitowanego przez żarówkę dla różnych napięć zasilających. Wyznaczenie dla każdego napięcia ogrzewającego odpowiedniego natężenia prądu i obliczenie oporu włókna. Określenie zależności oporu włókna od temperatury.

2. Podstawy teoretyczne:

Prawo Stefana-Boltzmanna - prawo fizyczne określające zależność całkowitej zdolności emisyjnej ε ciała doskonale czarnego od jego temperatury bezwzględnej T: ε = σT⁴, gdzie σ = 5,675 × 10^-8(W/m²)K⁴ (tzw. Stefana-Boltzmanna stała). Stefana-Boltzmanna prawo otrzymuje się przez scałkowanie prawa promieniowania Plancka (promieniowanie cieplne).

L(T)=

k= 1,381*10^-23 J/K - stała Stefana- Boltzmana

c= 3,00*10⁸ m/s - prędkość światła

h= 6,62*10^-34 Js - stała Plancka

Wzór można zapisać również w postaci:

L(T)=σT⁴

3.Opracowanie pomiarów

Doświadczenie rozpoczynamy od zestawienia schematu pomiarowego zgodnie z rysunkiem w celu wyznaczenia oporu włókna żarówki w temperaturze pokojowej.

Z pomiaru natężenia prądu i napięcia obliczamy opór włókna żarówki korzystając z prawa Ohma. Następnie obliczamy opór Ro dla t = 24 ^oC korzystając ze wzoru:

Ro=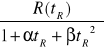

t_R=24^oC

α=4,82*10^-3 K^-1

β=6,76*10^-7 K^-2

R(t_R) - opór włókna żarówki w temperaturze pokojowej

I [mA]	U [mV]	Rtr [Ω]	Ro [Ω]
20	7,1	0,35500	0,31808058
40	14,3	0,35750	0,32032059
60	21,3	0,35500	0,31808058
80	28	0,35000	0,31360058
100	34,9	0,34900	0,31270458
120	41,6	0,34667	0,3106139
140	48,7	0,34786	0,31168057
160	54,5	0,34063	0,30520056
Odchylenie stand.		0,00548	0,00491349

Następnie zestawiamy układ gdzie opornik 100 Ω nie jest już częścią obwodu pomiarowego. Włókno jest teraz zasilane przez źródło napięcia przemiennego poprzez amperomierz umożliwiający pomiar prądu przemiennego do wartości 6 A. Woltomierz podłączony jest równolegle do włókna żarówki, a napięcie przemienne jest zwiększane z krokiem 1 V do wartości maksymalnej 8 V.

Korzystając z prawa Ohma obliczamy opór R(t)

U [V]	I [A]	Utherm [V]	R(t) [Ω]
1	2	0,19	0,51
2	2,73	1,01	0,73992674
3	3,34	2,42	0,90419162
4	3,86	4,13	1,04145078
5	4,36	6,25	1,15137615
6	4,83	8,75	1,24637681
7	5,24	11,4	1,33969466
8	5,65	13,9	1,41946903
Odchylenie standardowe			0,31123435

Z otrzymanych pomiarów obliczam temperaturę bezwzględną korzystając ze wzoru:

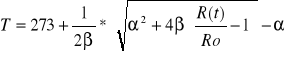
Po podstawieniu R(t) i Ro otrzymujemy:

R(t) [Ω]	Ro [Ω]	T [K]
0,51	0,31808058	396,05617
0,73992674	0,32032059	535,13789
0,90419162	0,31808058	636,73686
1,04145078	0,31360058	725,77272
1,15137615	0,31270458	791,69669
1,24637681	0,3106139	851,14696
1,33969466	0,31168057	901,83430
1,41946903	0,30520056	963,57269

Wykonujemy wykres funkcji:

U_therm=σT⁴

Po zlogarytmowaniu obustronnym przy podstawie 10 otrzymujemy:

log U_therm = 4logT + log σ

Sporządzony wykres wygląda następująco:

Z metody regresji liniowej odczytujemy wartości:

Współczynnik a= 4,827613768	SD= 0,123649274
Współczynnik b= -13,20610982	SD= 0,352080718
Nachylenie 4,827613768	Błąd bezwzględny Δ = 0,82
		Błąd względny δ = 0,170124481
Odchylenie standardowe krzywej	0,042502674

4. Wnioski

Zgodnie z prawem Stefana - Boltzmana energia emitowana przez ciało doskonale czarne na jednostkę powierzchni i w jednostce czasu jest proporcjonalna do czwartej potęgi temperatury bezwzględnej tego ciała. W doświadczeniu rolę ciała doskonale czarnego pełni rozżarzone włókno żarówki, którego emisja energii jest badana w funkcji temperatury. Doświadczenie rozpoczęliśmy od zestawienia obwodu pomiarowego celu wyznaczenia oporu włókna żarówki w temperaturze pokojowej. Natężenie prądu jest wystarczająco małe, aby zaniedbać efekt nagrzewania się żarówki. Podwojenie prądu powoduje dwukrotne zwiększenie napięcia. Niewielkie zmiany Ro tylko w małym stopniu wpływają na nachylenie S.

100 Ω

0…20 V DC

---