DOLNOŚLĄSKIE MECZE MATEMATYCZNE 2004/05
KATEGORIA: GIMNAZJA
¾ FINAŁU
Pośrodku Kwadratowego Stawu leży Kwadratowa Wyspa, patrz rysunek.
Pomysłowy Dobromir ma dwie deski długości 1945/2005 i chce z nich zbudować most prowadzący z brzegu na wyspę. Nie chce desek łamać ani kleić, ale może układać jedne na drugich. Czy to wykonalne?
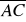
jest krótszą przekątną równoległoboku ABCD. W jakim stosunku dzieli ją odcinek poprowadzony z punktu B do środka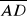
?
Oblicz
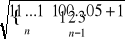
.
Jak sprytnie obliczyć za pomocą 10-cyfrowego kalkulatora dokładny wynik działania 12345678910111213⋅13121110987654321?
Ile różnych łamanych zamkniętych może wykreślić piłka rzucana kolejno co tyle samo osób w gronie n dziewcząt stojących w równych odstępach na obwodzie koła?
Model KLEP 2005 jest klepsydrą składającą się z trzech identycznych zbiorników rozmieszczonych symetrycznie, z których każdy jest połączony z dwoma pozostałymi. Po ustawieniu klepsydry na dowolnych dwóch zbiornikach zawartość górnego przesypuje się do nich równocześnie ze stałą prędkością. Jeśli górny pojemnik zawiera cały piasek z klepsydry, to na jego opróżnienie potrzeba 16 minut. Czy za pomocą tej klepsydry da się odmierzyć 9 minut?
Każdy z 20 honorowych członków Polskiego Towarzystwa Miłośników Nietoperzy zna co najmniej 10 honorowych członków. Udowodnij, że pewnych 4 honorowych członków można posadzić przy kwadratowym stole, tak by każdy siedział pomiędzy swoimi dwoma znajomymi. (Zakładamy, że relacja znajomości jest symetryczna, tzn. jeśli A zna B, to B zna A).
Liczby 1, 2, ..., 2005 rozmieszczono w dowolny sposób na okręgu. Możemy zamienić miejscami dwie sąsiednie liczby, jeśli moduł ich różnicy jest większy niż 1. Czy zawsze można w ten sposób ustawić je w porządku rosnącym zgodnie z ruchem wskazówek zegara?
Rozwiąż układ równań:
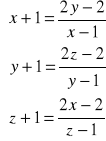
.
Dla jakich całkowitych k liczba
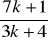
jest całkowita?
Oblicz pole wypukłego pięciokąta ABCDE, w którym boki AB=CD=EA=BC+DE=1, a kąty ABC i DEA są proste.
Wzdłuż 15-kilometrowego odcinka autostrady A0 rozmieszczono w równych odstępach reklamy Pewnej Firmy. Jadąc ze stałą prędkością, pani Magda zauważyła, że liczba reklam, które mija w ciągu minuty, pomnożona przez 15 jest dokładnie jej prędkością wyrażona w km/h. W jakiej odległości rozmieszczone są reklamy?
1
1
Wyszukiwarka
Podobne podstrony:
zadsg, nauczyciel szkoła podstawowa, matematyk
zadsg, nauczyciel szkoła podstawowa, matematyk
zadsg, nauczyciel szkoła podstawowa, matematyk
zadsp, nauczyciel szkoła podstawowa, matematyk
gim534, nauczyciel szkoła podstawowa, matematyk
gim5fin, nauczyciel szkoła podstawowa, matematyk
ge3, nauczyciel szkoła podstawowa, matematyk
sp5fin, nauczyciel szkoła podstawowa, matematyk
pe3, nauczyciel szkoła podstawowa, matematyk
zadsp, nauczyciel szkoła podstawowa, matematyk
zadsp, nauczyciel szkoła podstawowa, matematyk
ze3, nauczyciel szkoła podstawowa, matematyk
WSO matematyka, nauczyciel szkoła podstawowa, matematyk
zadsp, nauczyciel szkoła podstawowa, matematyk
dziennik zajec, mat podst, nauczyciel szkoła podstawowa
dla polonistów, nauczyciel szkoła podstawowa, polonista
Sprawdzian z edukacji matematycznej dla III klasy, Szkola podstawowa kl.3,4,5, Klasa 3, matematyka k
więcej podobnych podstron