Wybrane zagadnienia z Ekonometrii WSEI

1. Dobór zmiennych objaśniających do modelu liniowego

1.1. Uwagi wstępne

Zmienne objaśniające w modelu ekonometrycznym powinny się odznaczać następującymi własnościami:

Mieć odpowiednio wysoką zmienność;

Być silnie skorelowane ze zmienną objaśnianą;

Być silnie skorelowane ze zmienną objaśnianą;

Być słabo skorelowane między sobą;

Być silnie skorelowane z innymi zmiennymi nie pełniącymi roli zmiennych objaśniających, które zmienne objaśniające reprezentują (chodzi, by zmienne objaśniające były dobrymi reprezentantkami zmiennych, które nie weszły do zbioru zmiennych objaśniających).

Wybór zmiennych objaśniających do modelu ekonometrycznego odbywa się za pomocą metod statystycznych.

Procedura doboru jest następująca:

Na podstawie wiedzy merytorycznej sporządza się zestaw tzw. potencjalnych zmiennych objaśniających (zmiennych pierwotnych), którymi są wszystkie najważniejsze wielkości oddziałujące na zmienną objaśnianą. Zmienne te oznacza się jako X₁, X₂,...,X_m.

Gromadzi się dane statystyczne będące realizacjami zmiennej objaśnianej i potencjalnych zmiennych objaśniających. Otrzymuje się w ten sposób wektor y obserwacji zmiennej Y oraz macierz X obserwacji zmiennych X₁, X₂,...,X_m. o postaci:

,

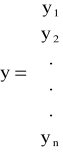
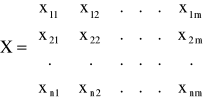
Eliminuje się potencjalne zmienne odznaczające się zbyt niskim poziomem zmienności.

Oblicza się współczynniki korelacji pomiędzy wszystkimi rozpatrywanymi zmiennymi.

Przeprowadza się redukcję zbioru potencjalnych zmiennych objaśniających za pomocą wybranej metody statystycznej.

1.2. Eliminowanie zmiennych quasi-stałych

Wstępnym warunkiem uznania różnych zmiennych za zmienne objaśniające modelu jest ich dostatecznie wysoka zmienność. Miarą poziomu zmienności jest współczynnik zmienności:

,

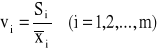
gdzie
- średnia arytmetyczna zmiennej X_i:
, natomiast S_i - odchylenie standardowe zmiennej X_i: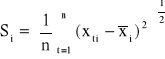
. Obiera się krytyczną wartość współczynnika zmienności v*, np., v*=0,10; następnie zmienne spełniające nierówność v_i≤v* uznaje się za quasi-stałe i eliminuje ze zbioru potencjalnych zmiennych objaśniających, gdyż zmienne te nie wnoszą istotnych informacji do modelu ekonometrycznego.

1.3. Wektor i macierz współczynników korelacji

Aby ocenić siłę liniowej zależności zmiennej objaśnianej Y i potencjalnych zmiennych objaśniających X₁, X₂, ..., X_m., oblicza się współczynnik korelacji:

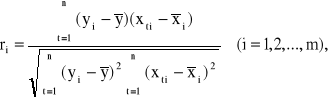
Współczynniki te są przedstawiane w postaci wektora korelacji: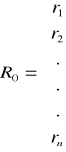
.

Współczynnik korelacji między potencjalnymi zmiennymi objaśniającymi X₁, X₂, ..., X_m. są obliczane według wzoru:

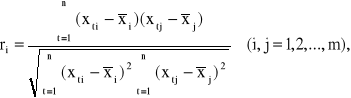
Współczynniki te tworzą macierz korelacji: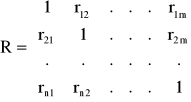
.

Macierz R jest symetryczna tzn. r_ij=r_ji.

1.5. Metoda wskaźników pojemności informacyjnej

Idea metody wskaźników pojemności informacyjnej sprowadza się do wyboru takich zmiennych objaśniających, które są silnie skorelowane ze zmienną objaśnianą, a jednocześnie słabo skorelowane ze sobą. Punktem wyjścia tej metody jest wektor R₀ i macierz R.

Rozpatruje się wszystkie kombinacje potencjalnych zmiennych objaśniających, których ogólna liczba wynosi: L=2^m-1. Dla każdej kombinacji zmiennych objaśniających oblicza się wskaźniki pojemności informacyjnej: indywidualne i integralne.

Indywidualne wskaźniki pojemności informacyjnej zmiennych w ramach rozpatrywanej kombinacji obliczane są następująco:

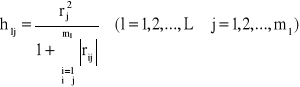
We wzorze tym l oznacza numer kombinacji, j oznacza numer zmiennej w kombinacji, natomiast m_l oznacza liczbę zmiennych w rozpatrywanej kombinacji.

Integralne wskaźniki pojemności informacyjnej kombinacji potencjalnych zmiennych objaśniających obliczane są według następującego wzoru:

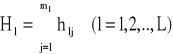
Indywidualne oraz integralne wskaźniki pojemności informacyjnej są unormowane w przedziale [0;1]. Przyjmują one tym większe wartości, im zmienne objaśniające są silniej skorelowane ze zmienną objaśnianą oraz im słabiej są skorelowane miedzy sobą.

Jako zmienne objaśniające wybiera się taką kombinację zmiennych, której odpowiada maksymalna wartość wskaźnika integralnej pojemności informacyjnej.

1.6. Współczynnik korelacji wielorakiej

Współczynnik korelacji wielorakiej jest miarą siły związku liniowego zmiennej objaśnianej Y ze zmiennymi objaśniającymi X₁, X₂,..., X_k. Zdefiniowany jest następująco:

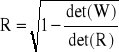
gdzie: det(R) - wyznacznik macierzy R współczynników korelacji zmiennych objaśniających X₁, X₂,..., X_k łączonych parami; det(W) - wyznacznik macierzy:

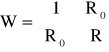
Wektor R₀ jest wektorem współczynników korelacji między zmienną Y i zmiennymi X₁, X₂,..., X_k. Macierz W w rozwiniętej postaci przedstawia się następująco:

Współczynnik korelacji wielorakiej jest unormowany w przedziale [0, 1]. Przyjmuje tym większe wartości, im związek zmiennej objaśnianej ze zmiennymi objaśniającymi jest silniejszy. Współczynnik korelacji wielorakiej może stanowić kryterium wyboru najlepszej kombinacji zmiennych objaśniających spośród jednakowo licznych kombinacji.

2. Szacowanie parametrów modeli liniowych metodą najmniejszych kwadratów

2.1.Uwagi wstępne

Szacowanie parametrów modelu ekonometrycznego sprowadza się do przypisywania nieokreślonym liczbowo parametrom konkretnych wartości liczbowych. Szacowanie to powinno być przeprowadzone w taki sposób, aby zapewniło najlepsze dopasowanie modelu do danych empirycznych. Powszechnie wykorzystywaną metodą szacowania parametrów liniowych modeli ekonometrycznych o postaci:

jest klasyczna metoda najmniejszych kwadratów. Idea metody sprowadza się do takiego wyznaczenia wartości ocen a₀, a₁,..., a_k parametrów strukturalnych α₀, α₁,..., α_k, aby suma kwadratów odchyleń zaobserwowanych wartości zmiennej objaśnianej od jej wartości teoretycznych obliczonych z modelu była najmniejsza. Warunek ten zapisuje się następująco:

gdzie e_t (t=1, 2, ..., n) - odchylenie empirycznych wartości zmiennej objaśnianej od jej wartości teoretycznych, nazywane resztami modelu:

, (t=1, 2, ..., n)

przy czym:
.

Zastosowanie metody najmniejszych kwadratów wymaga przyjęcia następujących założeń:

Szacowany model jest modelem liniowym;

Zmienne objaśniające są wielkościami nielosowymi o elementach ustalonych;

Nie występuje zjawisko współliniowości zmiennych objaśniających;

Składnik losowy ma wartość oczekiwaną równą zeru i stałą skończoną wariancję;

Nie występuje zjawisko autokorelacji składnika losowego, czyli zależność składnika losowego w różnych jednostkach czasu.

2.2. Szacowanie parametrów modelu z jedną zmienną objaśniającą

Liniowy model ekonometryczny z jedną zmienną ma ogólną postać:

Wartość ocen a oraz b parametrów strukturalnych α oraz β otrzymuje siκ w tym wypadku z warunku:

Po wyznaczeniu pochodnych cząstkowych funkcji S względem a oraz b i przyrównaniu ich do zera otrzymujemy tzw. układ równań normalnych:

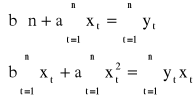
W wyniku rozwiązania układu równań normalnych otrzymujemy następujące wzory na oceny a oraz b:

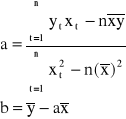
gdzie
oraz
oznaczają średnie arytmetyczne Y oraz X. Równoważny wzór na ocenę a ma postać:

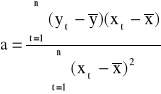
Wartość oceny a parametru α informuje, o ile jednostek zmieni się zmienna objaśniana Y, jeśli zmienna objaśniająca X zmieni się o jednostkę.

Specyficznym modelem liniowym z jedną zmienną objaśniającą jest liniowy model tendencji rozwojowej (trend liniowy) o postaci:

gdzie t oznacza zmienną czasową.

Wzory na oceny parametrów strukturalnych trendu liniowego są podobne do poprzednich z tym, że zamiast zmiennej X występuje zmienna czasowa t. W wypadku oceny a można także skorzystać z prostszego wzoru o postaci:

,

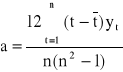
Wzór ten otrzymuje się z poprzednich wzorów przy uwzględnieniu następującej własności: jeżeli: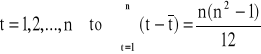

Ocenę wariancji odchyleń losowych modelu liniowego z jedną zmienną objaśniającą otrzymujemy ze wzoru:

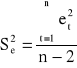
Wielkość S_e jest odchyleniem standardowym reszt modelu, które informuje, o ile zaobserwowane wartości zmiennej objaśnianej przeciętnie różnią się od teoretycznych wartości tej zmiennej wyznaczonych z modelu.

Standardowe błędy S(a) i S(b) szacunku parametrów strukturalnych α i β wyznacza siκ ze wzorσw:

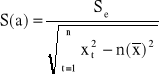
, lub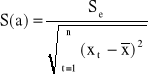

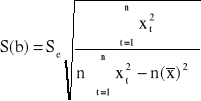
, lub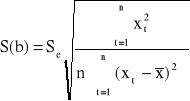

2.3.Szacowanie parametrów modelu z wieloma zmiennymi objaśniającymi

W celu przedstawienia klasycznej metody najmniejszych kwadratów w zastosowaniu do szacowania parametrów modelu z wieloma zmiennymi objaśniającymi:

wprowadzamy symbolikę macierzową:

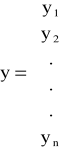
- wektor obserwacji zmiennej objaśnianej;

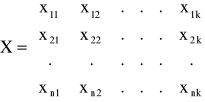
- macierz obserwacji zmiennych objaśniających;

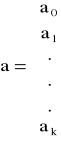
- wektor ocen parametrów strukturalnych;

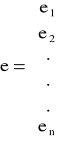
- wektor reszt modelu.

Kryterium najmniejszych kwadratów w tym wypadku można zapisać następująco:

,

gdzie:
.

Wzór na wektor a ocen parametrów strukturalnych modelu jest następujący:

Wariancję odchyleń losowych szacuje się na podstawie wzoru:

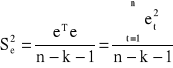
Macierz wariancji i kowariancji ocen parametrów strukturalnych szacuje się na podstawie wzoru:

.

W macierzy tej elementy na głównej przekątnej są wariancjami V(a_i) (i=0, 1, ..., k) ocen parametrów strukturalnych. Wielkości:

są standardowymi błędami szacunku parametrów strukturalnych.

3. Weryfikacja modeli liniowych

3.1.Uwagi wstępne

Po oszacowaniu parametrów modelu należy zbadać, czy zbudowany model dobrze opisuje badane zależności. Jeśli okaże się, że rozbieżność między otrzymanym modelem, a dymami empirycznymi lub między otrzymanym modelem a wiedzą ekonomiczną o badanych zależnościach jest duża, wówczas należy go skorygować oraz poprawić.

Przyczyny powodujące złą jakość modelu ekonometrycznego mogą się pojawiać już w początkowych etapach badanie ekonometrycznego. Nigdy nie ma pewności, czy zostały dobrane odpowiednie zmienne objaśniające. Wątpliwości może budzić także dobór analitycznej postaci modelu. W samym procesie estymacji mogła też być zastosowana niewłaściwa metoda szacowania parametrów. Wszystko to powoduje potrzebę przeprowadzenia weryfikacji modelu przed jego wykorzystaniem do wnioskowania o badanych zależnościach.

Weryfikacja modelu sprowadza się do zbadania trzech własności:

Stopnia zgodności modelu z danymi empirycznymi;

Jakości ocen parametrów strukturalnych;

Rozkładu odchyleń losowych.

3.2. Ocena dopasowania modelu do danych empirycznych

Ocena dopasowania modelu do danych empirycznych ma na celu sprawdzenie, czy model ten w wystarczająco wysokim stopniu wyjaśnia kształtowanie się zmiennej objaśnianej. Do tego celu służą różne miary zgodności modelu z danymi empirycznymi. Podstawowymi miarami tego typu są: odchylenie standardowe reszt, współczynnik zmienności losowej, współczynnik zbieżności i współczynnik determinacji.

Współczynnik zmienności losowej jest zdefiniowany następująco:

Współczynnik ten informuje, jaki procent średnia arytmetycznej zmiennej objaśnianej modelu stanowi odchylenie standardowe reszt. Mniejsze wartości współczynnika W_e wskazują na lepsze dopasowanie modelu do danych empirycznych.

Jeśli dla założonej z góry krytycznej wartości współczynnika zmienności losowej W* (np. W*=10%) zachodzi nierówność:
, to model uznaje się za dostatecznie dobrze dopasowany do danych empirycznych. Przy przeciwnym kierunku nierówności dopasowanie uznaje się za zbyt słabe. Współczynnik zmienności losowej ma także zastosowanie przy przeprowadzaniu porównania stopnia zgodności z danymi empirycznymi modeli opisujących się kształtowanie różnych zmiennych objaśnianych.

Współczynnik zbieżności wyraża się wzorem:

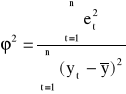
Współczynnik zbieżności przyjmuje wartości z przedziału [0; 1]. Informuje on jaka część całkowitej zmienności zmiennej objaśnianej nie jest wyjaśniona przez model. Dopasowanie modelu do danych jest tym lepsze, im współczynnik zbieżności jest bliższy zeru.

Współczynnik determinacji ma postać:

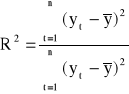
Współczynnik determinacji przyjmuje wartości z przedziału [0;1]. Informuje on, jaką część całkowitej zmienności zmiennej objaśnianej stanowi zmienność wartości teoretycznych tej zmiennej, tj. część zdeterminowana przez zmienne objaśniające. Dopasowanie modelu do danych jest tym lepsze, im współczynnik determinacji jest bliższy jedności.

Między współczynnikami zbieżności i determinacji zachodzi relacja:

Pierwiastek kwadratowy ze współczynnika determinacji, tj. R, jest znanym współczynnikiem korelacji wielorakiej.

Aby stwierdzić, czy dopasowanie modelu do danych empirycznych jest dostatecznie duże, można zweryfikować hipotezę o istotności współczynnika korelacji wielorakiej tj. hipotezę zerową postaci:

wobec hipotezy alternatywnej
. Sprawdzianem tej hipotezy jest statystyka:

Statystyka ta ma rozkład F Fishera-Snedecora o m₁=k oraz m₂=n-k-1 stopniach swobody. Z tablic testu F dla zadanego poziomu istotności γ oraz m₁ i m₂ stopni swobody odczytuje się wartość krytyczną F*. Jeśli F≤F*, to nie ma podstaw do odrzucenia hipotezy H₀. Oznacza to, że współczynnik korelacji wielorakiej jest nieistotnie różny od zera, a dopasowanie modelu do danych jest zbyt słabe. Natomiast jeśli F>F*, to hipotezę H₀ należy odrzucić na rzecz hipotezy H₁. Współczynnik korelacji wielorakiej jest istotny, a stopień dopasowania modelu do danych jest dostatecznie wysoki.

3.3. Badanie istotności parametrów strukturalnych

Badanie istotności parametrów strukturalnych α₁, α_2,..., α_k, liniowego modelu ekonometrycznego ma na celu sprawdzenie, czy zmienne objaśniające istotnie oddziaływają na zmienną objaśnianą, czy też nie. Dla każdego i=1,2,...,k weryfikuję się hipotezę zerową H₀: [α_i=0] wobec hipotezy alternatywnej H₁: [α_i≠0]. Sprawdzianem tej hipotezy jest statystyka:

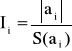
gdzie a_i - wartość oceny parametru strukturalnego α_i; S(a_i) - standardowy błąd szacunku tego parametru.

Z tablic testu t-Studenta dla przyjętego poziomu istotności γ oraz dla n-k-1 stopni swobody odczytuje się wartość krytyczną I*. Jeśli I_i ≤I*, nie ma podstaw do odrzucenia hipotezy H₀. Parametr strukturalny α_i różni się nieistotne od zera, a zmienna objaśniająca X_i nie wpływa w istotny sposób na zmienną objaśnianą Y. Natomiast jeśli I_i>I*, hipotezę H₀ należy odrzucić na rzecz hipotezy H₁. W tym przypadku parametr α_i różni się w sposób istotny od zera i zmienna objaśniająca X_i oddziaływuje w sposób istotny na zmienną objaśnianą Y.

3.4. Określanie relatywnego wpływu zmiennych objaśniających na zmienną objaśnianą

Ponieważ nie wszystkie zmienne objaśniające X_1, X₂,...,X_k mają jednakowy wpływ na zmienną objaśnianą Y, należy przeprowadzić ocenę relatywnego znaczenia tych zmiennych w modelu ekonometrycznym dla wyjaśnienia kształtowania się zmiennej objaśnianej.

Miarą relatywnego znaczenia zmiennej objaśniającej X_i w wyjaśnianiu zmian zmiennej objaśnianej Y jest współczynnik “ważności” b_i zdefiniowany następująco:

, (i=1,2,...,k)

gdzie
- średnia arytmetyczna zmiennej objaśniającej X_i;
- średnia arytmetyczna zmiennej objaśnianej Y; a_i - wartość oceny parametru strukturalnego α_i.

Większe wartości modułu współczynnika wartości b_i wskazują na relatywnie większy wpływ danej zmiennej objaśniającej na zmienną objaśnianą modelu.

4. Modele nieliniowe sprowadzalne do liniowych

4.1. Wybór postaci analitycznej modelu na podstawie apriorycznej wiedzy o badanych zależnościach

Przy nadawaniu określonej postaci analitycznej modelowi mającemu opisywać zależność między pewnymi zjawiskami ekonomicznymi często korzysta się z wiedzy ekonomicznej o badanych prawidłowościach. Istnieją pewne teorie ekonomiczne dotyczące zachowania się gospodarki narodowej, rynku czy przedsiębiorstw produkcyjnych, które mogą być podstawą sformułowania hipotezy, że pewna zależność może być w przybliżeniu opisana za pomocą funkcji o określonej postaci analitycznej.

4.2. Wybór postaci analitycznej modelu na podstawie wykresów rozrzutu punktów empirycznych

Metodę tę stosuje się zwłaszcza do modeli z jedną zmienną objaśniającą, a wiec modeli typu:

Dobór postaci modelu odbywa się na podstawie oceny wzrokowej rozrzutu punktów empirycznych o współrzędnych:

odpowiadającym wynikom obserwacji zmiennych Y i X przedstawionych na prostokątnym układzie współrzędnych.

Najczęściej spotykane typy związków nieliniowych łączące dwa zjawiska Y i X przedstawiono poniżej.

Omawiana metoda może być także adaptowana do modeli z wieloma zmiennymi objaśniającymi. W tym wypadku sporządza się k wykresów przedstawiających związki łączące zmienną objaśnianą z pojedynczymi zmiennymi objaśniającymi X₁, X₂, ....,X _k. Następnie nadaje się postacie analityczne funkcjom regresji zmiennej objaśnianej względem pojedynczych zmiennych objaśniających dbając jednocześnie o to, aby były to funkcje liniowe względem parametrów strukturalnych i ewentualnie nieliniowe względem zmiennych objaśniających. Postulat ten spełnia następujące funkcje regresji jednej zmiennej objaśniającej

• liniowa
  

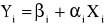
• hiperboliczna
  

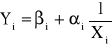
• logarytmiczna
  

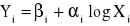
• wielomianowa
  

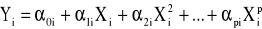
Funkcje te obrazują najczęściej spotykane w badaniach empirycznych typy związków łączących zjawiska ekonomiczne.

Model ekonometryczny powstaje przez zsumowanie tych części szczegółowych funkcji regresji, które są przy zmiennych objaśniających, oraz wyrazu wolnego. Można to zapisać następująco:

Jest to model liniowy względem parametrów strukturalnych i ewentualnie nie liniowy względem zmiennych objaśniających.

4.3. Dobór zmiennych objaśniających

Dobór zmiennych objaśniających do modelu nieliniowego względem zmienny objaśniających, a jednocześnie liniowego względem parametrów strukturalnych może być przeprowadzony na odstawie wektora współczynników korelacji zmiennej objaśnianej z liniowymi przekształceniami potencjalnych zmiennych objaśniających i macierzy współczynników korelacji między liniowymi przekształceniami potencjalnych zmiennych objaśniających. Jednej potencjalnej zmiennej objaśniającej może być przyporządkowane jedno przekształcenie liniowe lub kilka przekształceń liniowych.

W podobny sposób może być przeprowadzony dobór zmiennych objaśniających do potęgowego modelu ekonometrycznego:

Model ten sprowadza się do postaci liniowej przez jego obustronne zlogarytmowanie

logY= logα₀+α₁logX₁+α₂logX₂+...+α_klogX_k

W podstawieniach:

V=logY, β=logα₀, Z₁=logX₁, Z₂=logX₂, ..., Z_k=logX_k

otrzymujemy model liniowy zmiennej V względem zmiennych Z ₁,Z ₂, ..., Z _k o postaci:

W tym wypadku zmienne objaśniające dobiera się na podstawie wektora współczynników korelacji między logarytmami zmiennej objaśnianej i logarytmami potencjalnych zmiennych objaśniających oraz macierzy współczynników korelacji między logarytmami potencjalnych zmiennych objaśniających.

4.4. Szacowanie parametrów

Metoda najmniejszych kwadratów ma bezpośrednie zastosowanie do szacowania parametrów modeli liniowych, w których zmienna objaśniana jest liniową funkcją zmiennych objaśniających i odchyleń losowych. Jeśli zbudowany model jest modelem nieliniowym, to należy dokonać jego transformacji liniowej tak, aby przekształcone równanie miało postać liniową względem parametrów strukturalnych lub względem pewnych ich funkcji. Najpierw za pomocą metody najmniejszych kwadratów szacuje się parametry modelu przekształconego, przy czym wszelkie związane z tym rachunki są wykonywane na wartościach przekształconych zmiennych. Następnie oblicza się wartości ocen modelu pierwotnego.

4.5. Badanie dopasowania modelu do danych empirycznych

Miary dopasowania modeli do danych empirycznych mają zastosowanie do oceny modeli liniowych oraz modeli nieliniowych ze względu na parametry strukturalne.

Ocena dopasowania do danych empirycznych modeli nieliniowych ze względu zarówno na zmienne objaśniające jak i na parametry strukturalne może być przeprowadzana za pomocą wskaźnika średniego względnego poziomu reszt o postaci:

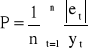
Im mniejsze są wartości wskaźnika P, tym lepsze dopasowanie modelu do danych empirycznych.

8. Modele wielorównaniowe

8.1. Uwagi wstępne

Wielorównaniowe modele ekonometryczne opisują kształtowanie się wielu zjawisk ekonomicznych, przy czym każde równanie modelu wielorównaniowego wyjaśnia zachowanie się jednego zjawiska.

Zjawiska ekonomiczne wyjaśniane przez model wielorównaniowy nazywają się zmiennymi endogenicznymi. Zjawiska ekonomiczne, które nie są wyjaśniane przez model i służą do wyjaśniania zmiennych endogenicznych nazywają się zmiennymi egzogenicznymi. Zmienne endogeniczne bez opóźnień czasowych nazywają się zmiennymi łącznie współzależnymi; oznaczamy je jako Y₁, Y₂, ...,Y_m. Zmienne endogeniczne z opóźnieniami czasowymi oraz zmienne egzogeniczne (bez opóźnień i z opóźnieniami) nazywają się zmiennymi z góry ustalonymi; oznacza się je jako Z₁, Z₂, ..., Z_k.

Ogólny zapis modelu wielorównaniowego jest następujący:

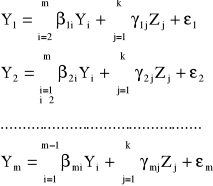
8.2. Postać strukturalna i postać zredukowana modelu

Macierzowe przedstawieni powyższego modelu wielorównaniowego nosi nazwę postaci strukturalnej. Aby otrzymać tę postać, należy przenieść wszystkie wyrazy modelu na lewą stroną, a po prawej stronie pozostawić jedynie odchylenia losowe. Postać strukturalna modelu wielorównaniowego jest następująca:

gdzie:

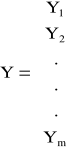
- wektor (m x 1) zmiennych endogenicznych bez opóźnień czasowych;

- macierz (m x m) parametrów przy zmiennych endogenicznych bez opóźnień czasowych;

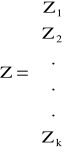
- wektor (k x 1) zmiennych z góry ustalonych;

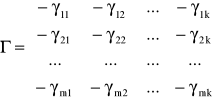
- macierz (m x k) parametrów przy zmiennych z góry ustalonych;

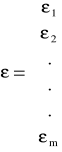
- wektor (m x 1) odchyleń losowych.

Jeśli nieopóźnione w czasie zmienne endogeniczne Y₁, Y₂, ...,Y_m wyrazimy jedynie poprzez zmienne z góry ustalone całego modelu Z₁, Z₂, ...,Z_k, to otrzymamy postać zredukowaną modelu:

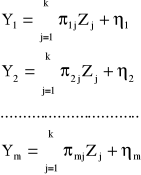
Macierzowy zapis postaci zredukowanej jest następujący:

- macierz (m x k) parametrów postaci zredukowanej przy zmiennych z góry ustalonych;

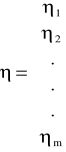
- wektor (m x 1) odchyleń losowych postaci zredukowanej.

Między parametrami postaci zredukowanej i postaci strukturalnej istnieją następujące zależności:

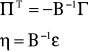
8.3. Klasyfikacja modeli wielorównaniowych

Ze względu na powiązania miedzy nieopóźnionymi w czasie zmiennymi endogenicznymi modele wielorównaniowe klasyfikuje się na: modele proste, modele rekurencyjne i modele o równaniach współzależnych. Klasyfikacja ta jest istotna z punktu widzenia metody szacowania parametrów. Rozpoznania klasy modelu wielorównaniowego dokonuje się w drodze badania własności macierzy B parametrów strukturalnych znajdujących się przy zmiennych endogenicznych bez opóźnień czasowych.

Jeżeli macierz B jest macierzą diagonalną, lub okaże się taką po przenumerowaniu równań modelu, to model nazywamy prostym. W modelach tej klasy nie występują powiązania między nieopóźnionymi w czasie zmiennymi endogenicznymi. Zmienne te nie występują w żadnym z równań w roli zmiennych objaśniających.

Jeżeli macierz B jest macierzą trójkątną lub okaże się taka po przenumerowaniu równań modelu albo po zmianie miejsca zmiennych w równaniach, to model nazywamy rekurencyjnym. W modelach tej klasy w danym równaniu w roli zmiennych objaśniających mogą występowa tylko te nieopóźnione w czasie zmienne endogeniczne, które we wcześniejszych równaniach pełniły rolę objaśnianych.

Jeżeli w wyniku przenumerowania równań lub zmiany miejsca zmiennych w równaniach nie otrzymamy z macierzy B ani macierzy diagonalnej, ani macierzy trójkątnej, to model jest modelem o równaniach współzależnych. W modelach tej klasy nieopóźnione w czasie zmienne endogeniczne mogą w dowolnym równaniu pełnić rolę zmiennych objaśniających.

8.4. Szacowanie parametrów modeli prostych i rekurencyjnych

W wielorównaniowych modelach prostych i rekurencyjnych nie występują sprzężenia zwrotne między nieopóźnionymi w czasie zmiennymi endogenicznymi. Dlatego każde równanie tych modeli można rozpatrywać osobno i traktować jako model jednorównaniowy. Parametry każdego równania mogą być szacowane klasyczną metodą najmniejszych kwadratów.

8.5. Identyfikowalność modeli o równaniach współzależnych

Przed przystąpieniem do szacowania parametrów modeli o równaniach współzależnych należy zbadać identyfikowalność poszczególnych równań. Jeśli równanie jest identyfikowalne, to można oszacować jego parametry. Jeśli równanie nie jest identyfikowalne, to nie można oszacować jego parametrów. Cały model o równaniach współzależnych jest identyfikowalny, jeśli wszystkie jego równania są identyfikowalne.

Twierdzenie: Warunkiem koniecznym i dostatecznym tego, aby i-te równanie wchodzące w skład modelu o m równaniach współzależnych było identyfikowalne, jest by macierz A_i parametrów znajdujących się przy zmiennych, które są w modelu, a nie występują w równaniu, którego identyfikowalność jest badana, była rzędu m-1.

Niech k_i oznacza liczbę zmiennych, które znajdują się w modelu, a nie występują w równaniu, którego identyfikowalność jest badana. Jeśli k_i=m-1, to równanie jest jednoznacznie identyfikowalne. Jeśli k_i>m-1, to równanie jest niejednoznacznie identyfikowalne. Jeśli k_i<m-1, to równanie nie jest identyfikowalne. Rozróżnienie to jest istotne z punktu widzenia metody szacowania parametrów modelu o równaniach współzależnych.

8.6. Pośrednia metoda najmniejszych kwadratów

Pośrednia metoda najmniejszych kwadratów ma zastosowanie do szacowania parametrów modeli o równaniach współzależnych jednoznacznie identyfikowalnych. Metoda ta może być także stosowana do szacowania parametrów pojedynczych równań jednoznacznie identyfikowalnych wchodzących w skład modelu o równaniach współzależnych. Idea pośredniej metody najmniejszych kwadratów polega na wykorzystaniu ocen parametrów postaci zredukowanej do uzyskania ocen parametrów postaci strukturalnej.

Procedura pośredniej metody najmniejszych kwadratów jest następująca:

1. Sprowadza się model do postaci zredukowanej:

2. Parametru postaci zredukowanej szacuje się klasyczną metodą najmniejszych kwadratów wykorzystując wzór:

gdzie:

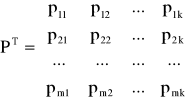
- ocena macierzy
parametrów postaci zredukowanej;

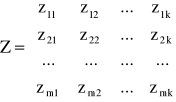
- macierz obserwacji zmiennych z góry ustalonych występujących w modelu;

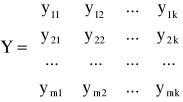
- macierz obserwacji zmiennych łącznie współzależnych występujących w modelu.

Można również szacować parametry każdego równania zredukowanego oddzielnie na podstawie wzoru:

(i=1,2,...,m)

gdzie:

- wektor ocen parametrów i-tego równania postaci zredukowanej,

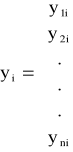
- wektor obserwacji zmiennej łącznie współzależnej, pełniącej rolę zmiennej objaśnianej w szacowanym równaniu.

3. Oceny parametrów postaci strukturalnej rozwiązuje się w drodze rozwiązywania układu równań:

Jeśli szacuje się parametry pojedynczego, l-tego, równania modelu, oceny parametrów β_il oraz γ_jl znajduje się w drodze przyrównania do siebie elementów l-tego wiersza macierzy BP^T i l-tego wiersza macierzy
.

8.7. Podwójna metoda najmniejszych kwadratów

Podwójna metoda najmniejszych kwadratów służy do oszacowania parametrów równań modeli o równaniach współzależnych zarówno jednoznacznie, jak i niejednoznacznie identyfikowalnych. Parametry każdego równania szacuje się oddzielnie.

Niech i oznacza numer szacowanego równania. W równaniu tym występuje h zmiennych endogenicznych bez opóźnień czasowych, przy czym h-1 niech pełni rolę zmiennych objaśniających. Ponadto w szacowanym równaniu występuje f zmiennych z góry ustalonych. Szacowane równanie przedstawia się następująco:

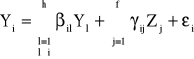
Idea podwójnej metody najmniejszych kwadratów polega na tym, że zmienne łącznie współzależne Y₁, Y₂, ...,Y_i-1,Y_i+1,...,Y_h występujące w danym równaniu w roli zmiennych objaśniających wyraża się przez zmienne z góry ustalone modelu Z₁, Z₂,...,Z_k, co jest równoznaczne z wyznaczeniem postaci zredukowanej:

(l=1,2,...,i-1,i+1,...,h)

Parametry postaci zredukowanej szacuje się metodą najmniejszych kwadratów korzystając ze wzoru:

gdzie Z - macierz (n x k) obserwacji zmiennych z góry ustalonych całego modelu; Y_i - macierz [n x (h-1)] obserwacji zmiennych łącznie współzależnych występujących w szacowanym równaniu w roli zmiennych objaśniających; P_i - macierz [k x (h-1)] ocen parametrów postaci zredukowanej zmiennych łącznie współzależnych występujących w szacowanym równaniu w roli zmiennych objaśniających.

Na podstawie oszacowanej postaci zredukowanej oblicza się teoretyczne wartości zmiennych łącznie współzależnych występujących w szacowanym równaniu w roli zmiennych objaśniających:

gdzie:
- macierz [n x (h-1)] wartości teoretycznych tych zmiennych.

Oszacowane zmienne łącznie współzależne, pełniące w danym równaniu rolę zmiennych objaśniających, wstawia się do tego równania tak, że otrzymuje się równanie o postaci:

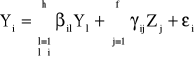
Parametry tego równania szacuje się metodą najmniejszych kwadratów korzystając ze wzoru:

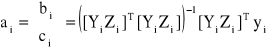
gdzie: a_i - wektor [(h-1+f) x 1] ocen parametrów strukturalnych szacowanego równania; b_i - wektor [(h-1) x 1] ocen parametrów strukturalnych przy zmiennych łącznie współzależnych występujących w szacowanym równaniu w roli zmiennych objaśniających; c_i - wektor (f x 1) ocen parametrów strukturalnych przy zmiennych z góry ustalonych w szacowanym równaniu; Z_i - macierz (n x f) obserwacji zmiennych z góry ustalonych w szacowanym równaniu; y_i - wektor (n x 1) obserwacji zmiennej endogenicznej bez opóźnień czasowych, pełniącej rolę zmiennej objaśnianej.

Wzór powyższy można zapisać w postaci równoważnej jako:

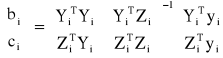
Wariancję odchyleń losowych danego równania szacuje się na podstawie wzoru:

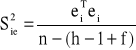
gdzie e_i oznacza wektor reszt szacowanego równania.

Oceną macierzy wariancji i kowariancji ocen parametrów strukturalnych szacowanego równania jest:

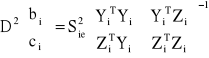
2

1

X

Y

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

3

3

2

2

1

0

x

x

x

Y

ˆ

















X

Y

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

2

2

1

0

x

x

Y

ˆ













X

Y

•

•

•

•

•

•

•

•

•

•

•

•

•

•

x

1

Y

ˆ









•

•

x

x

x

Y

ˆ









X

Y

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

X

Y

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

•

x

sin

Y

ˆ









X

Y

•

•

•

•

•

•

•

•

•

•

•

•

•

•

)

1

(

x

Y

ˆ











x

log

a

Y

ˆ







X

Y

•

•

•

•

•

•

•

•

•

•

•

•

•

•

)

1

(

x

Y

ˆ











x

a

Y

ˆ





•

•

X

Y

•

•

•

•

•

•

•

•

•

•

•

•

x

e

1

Y

ˆ









γ



2

2

1

0

x

x

Y

ˆ













x

x

1

Y

ˆ









---