Edward Osada

Wykłady z geodezji i geoinformatyki

3

Osnowy geodezyjne

UxLan

Wrocław 2010

Druk publikacji wykonano zgodnie z oryginałami tekstów, tablic i rysunków
dostarczonych przez autora w formacie PDF.
Wydawca nie ponosi odpowiedzialności za ich treść, formę i styl.



Copyright by Edward Osada, 2010

Redakcja:

Joanna Tyniów

Wydanie I

ISBN 978-83-60221-02-0

Zamówienia prosimy kierować pod adresem Wydawcy:

UxLan Firma Informatyczna Józef Osada
ul. Wiosenna 17a
53-017 Wrocław
tel. [phone]

lub e-mailem: [e-mail]

Druk i oprawa:

GS MEDIA. SZYBKI DRUK CYFROWY
ul. Wałbrzyska 9E, 52-314 Wrocław
tel./fax [phone]
e-mail: [e-mail]
www.gsmedia.com.pl

2

Spis tre

ś

ci

Wstęp

5

1. Wprowadzenie do rachunku wyrównawczego

7

1.1. Klasyfikacja błędów pomiarowych

7

1.2. Błędy systematyczne

8

1.3. Błędy przypadkowe

9

1.4. Wartość średnia

10

1.5. Średnia ważona

12

1.6. Średnia odporna

14

1.7. Rozkład normalny

17

1.8. Obserwacje zależne

20

1.9. Błąd funkcji obserwacji

25

2. Osnowy wysokościowe

53

2.1. Podział i klasyfikacja

53

2.2. Znaki punktów

57

2.3. Projektowanie

62

2.4. Pomiar

70

2.5. Wyrównanie sieci niwelacyjnej

80

2.6. Wpasowanie sieci do punktów dowiązania

93

2.7. Wpasowanie sieci do przystających punktów dowiązania

99

2.8. Dołączanie dodatkowych ciągów

105

2.9. Wyrównywanie sieci w czasie pomiaru

107

2.10. Wstępna analiza dokładności sieci

114

2.11. Wyrównanie sieci swobodnej

118

3. Osnowy poziome

127

3.1. Podział i klasyfikacja

127

3.2. Znaki punktów

133

3.3. Projektowanie

139

3.4. Pomiar

145

3.5. Wyrównanie wcięcia liniowego wielokrotnego

157

3.6. Wyrównanie wcięcia kątowo liniowego w przód

165

3.7. Wyrównanie wcięcia kątowo liniowego wstecz

173

3.8. Wyrównanie ciągu i sieci poligonowej

181

3.9. Wyrównanie sieci kątowo liniowej

193

3.10. Wpasowanie sieci do punktów dowiązania

208

3.11. Wpasowanie sieci do przystających punktów dowiązania

211

3.12. Wyrównywanie sieci w czasie pomiaru

212

3.13. Wstępna analiza dokładności sieci

216

3.14. Osnowa dwufunkcyjna

217

Literatura

223

3

4

Wst

ę

p

Geodezja jest nauką o pomiarach Ziemi, wykonywanych w celu:

wyznaczenia kształtu i ruchu obrotowego Ziemi,

•

wyznaczenia pola siły ciężkości i geoidy,

•

sporządzania map,

•

obsługi budownictwa,

•

obsługi gospodarki nieruchomościami.

•

zakładania Krajowego Systemu Informacji o Terenie, jako podstawy Infrastruktury

•

Informacji Przestrzennej w Polsce

Zagadnienia te są realizowane za pomocą:

technik pomiarowych geodezji kosmicznej i satelitarnej,

•

technik pomiarowych fotogrametrii satelitarnej, lotniczej i bliskiego zasięgu,

•

pomiarów przy użyciu tachimetrów, niwelatorów, skanerów i grawimetrów.

•

Książki Wykłady z geodezji i geoinformatyki zawierają treści programowe wykładane
na kierunku studiów geodezja i kartografia w zakresie geodezyjnych pomiarów
szczegółowych, geodezji fizycznej, satelitarnej i inżynieryjnej, astronomii geodezyjnej,
rachunku wyrównawczego, fotogrametrii i systemów informacji przestrzennej GIS.

Dotychczas ukazały się:

1. Niwelacja

elementy obsługi niwelatorów klasycznych i kodowych

•

zakładanie osnów pomiarowych wysokościowych

•

wykonywanie pomiarów wysokościowych

•

niwelacja punktów rozproszonych, siatkowa i profilów

•

2. Tachimetria

elementy obsługi tachimetrów

•

zakładanie osnów pomiarowych sytuacyjnych

•

wykonywanie pomiarów sytuacyjnych i wysokościowych

•

komputerowe kreślenie mapy zasadniczej

•

skanowanie, georeferencja i wektoryzacja mapy zasadniczej.

•

3. Osnowy geodezyjne

projektowanie, stabilizacja punktów, pomiar i wyrównanie osnów poziomych,

•

wysokościowych i dwufunkcyjnych

Opisy metod pomiarowych są ilustrowane przykładami liczbowymi w programach
komputerowych Mathcad, C-Geo, ArcGIS, TNTmips, Geomatica, PG-STEAMER
i innych.

Wrocław, październik 2010

5

6

Wprowadzenie
do rachunku
wyrównawczego

1

1.1. Klasyfikacja bł

ę

dów pomiarowych

Pomiar

Pomiar jest czynnością mającą na celu wyznaczenie wartości danej wielkości fizycznej.
Podczas pomiaru dokonuje się porównania wartości mierzonej wielkości fizycznej
z wartością wzorcową, na przykład metra, kąta, temperatury itp. Wynikiem pomiaru jest
wskazanie narzędzia pomiarowego wyskalowanego w jednostkach miary mierzonej
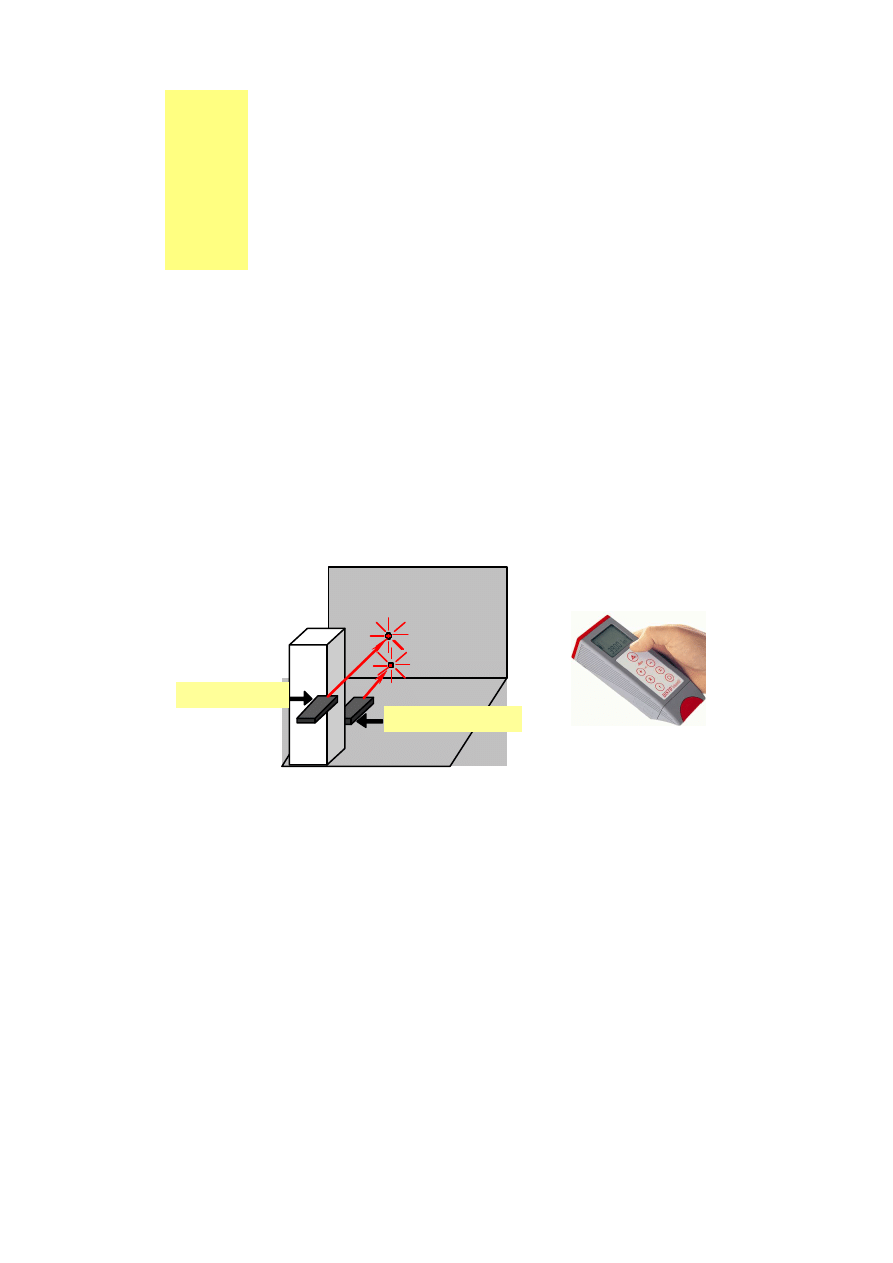
wielkości - długości, kąta, temperatury itp. Przykładem są pomiary długości budynku,
jak również odległości między ścianami, posadzką a sufitem wykonywane za pomocą
ręcznego dalmierza laserowego (rys.1.1.1). W tym przypadku odległość d jest obliczana
na podstawie zależności 2d = ct gdzie c - prędkość światła, t - czas przebiegu promienia
ś

wietlnego od dalmierza do mierzonego punktu i z powrotem.

d = 4,006m

±

2mm

4,507m

±

2mm

DISTO

Leica DISTO

Rys. 1.1.1

Wyniki pomiarów mogą być obciążone błędami:

grubymi - zwykle są to omyłki podczas edycji wyników pomiarów,

•

systematycznymi - które można wyznaczyć i wyeliminować z wyników pomiarów:

•

- instrumentalne - wynikają z niedokładności wykonania narzędzi pomiarowych,

- środowiskowe - wynikają z wpływu środowiska,

przypadkowymi - których wielkości i znaku nie można wyznaczyć przed

•

wykonaniem pomiaru.

7

1.2. Bł

ę

dy systematyczne

Bł

ę

dy systematyczne instrumentalne i

ś

rodowiskowe

Wyniki pomiarów są zwykle obciążone błędami systematycznymi, wynikającymi
z niedokładności wykonania narzędzi pomiarowych jak również wpływu środowiska.

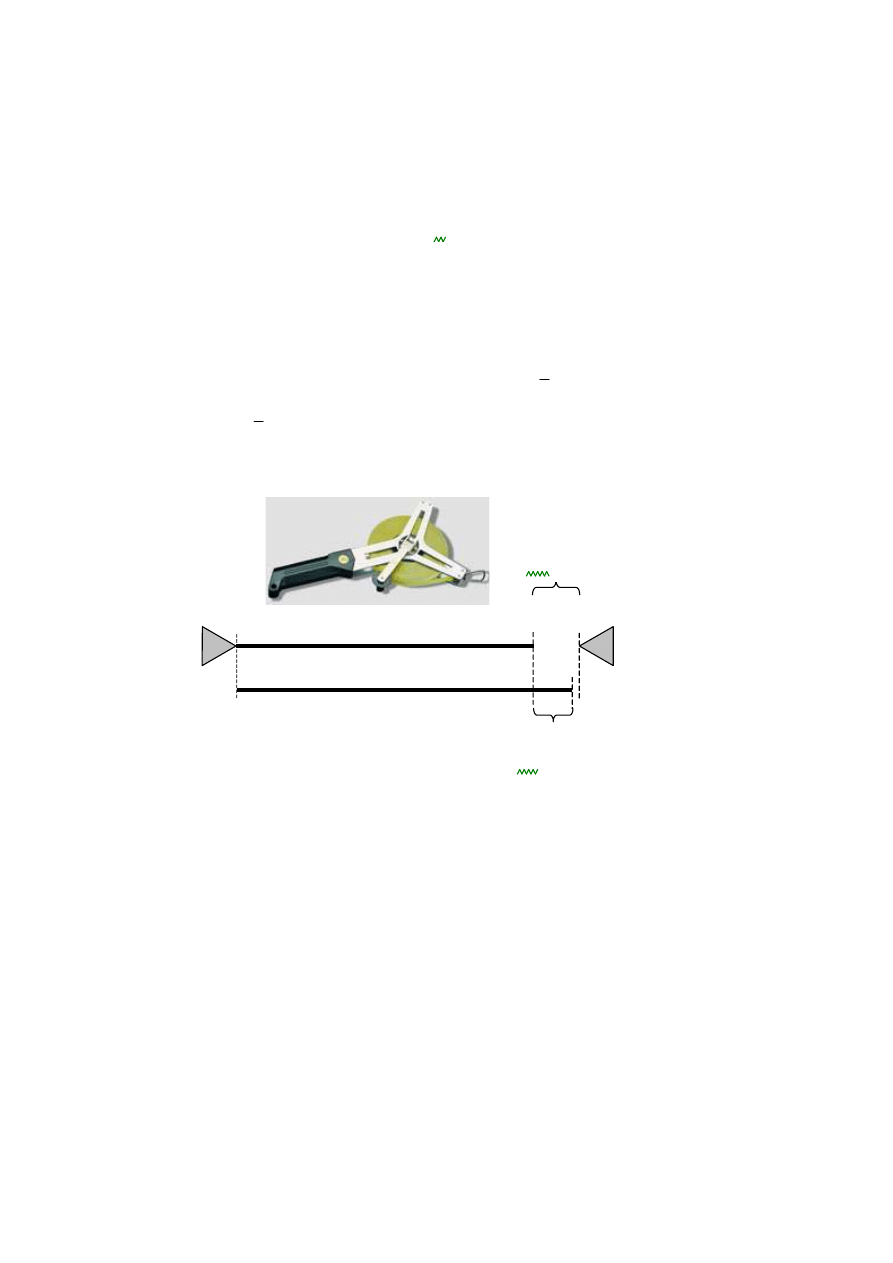
Na przykład taśma o długości nominalnej

l

20

:=

m ustalonej przez producenta jest

poddawana okresowej komparacji, w wyniku której jest ustalana poprawka
komparacyjna taśmy

pk

0.004

:=

(rys. 1.2.1). Różnica temperatury w czasie pomiaru i

podczas komparacji powoduje wydłużenie taśmy, nazywane poprawką termiczną

pt

0.0021

:=

(rys. 1.2.1). Zatem, do wyniku pomiaru za pomocą taśmy o długości l

dodaje się poprawkę termiczną i komparacyjną, proporcjonalnie do zmierzonej długości

d. Np. dla

d

10.01

:=

poprawka komparacyjna wynosi

pk

d

l

⋅

0.002

=

, natomiast

termiczna

pt

d

l

⋅

0.001

=

. Poprawka komparacyjna i poprawka termiczna taśmy są

błędami systematycznymi pomiaru odległości, odpowiednio instrumentalnym
i środowiskowym.

0

Długość nominalna taśmy wg. producenta l = 20 m

20 m

Temperatura w czasie komparacji t

k

= 20°C

C

Temperatura w czasie pomiaru terenowego
np. t = 29°C

Poprawka komparacyjna, np.

Poprawka termiczna

r = 0.0000115 m/°C - współczynnik
rozszerzalności liniowej stali.

pk

0.004

:=

m

r

0.0000115

:=

t

29

:=

tk

20

:=

pt

r t

tk

−

(

)

⋅

l

⋅

:=

Rys. 1.2.1.

pt 0.0021

=

m

Innym przykładem jest błąd systematyczny w pomiarach laserowych odległości za
pomocą tachimetrów, nazywany poprawką meteorologiczną. Wysyłany przez dalmierz
tachimetru promień laserowy ma prędkość określoną dla ustalonej wartości temperatury
powietrza i ciśnienia atmosferycznego np. 20

°

C i 1025 hPa. Ze zmianą temperatury

i ciśnienia ulega zmianie prędkość światła w atmosferze, co ma wpływ na wynik
pomiaru odległości. Zatem pomierzona odległość jest przeskalowywana M*d , gdzie
skala M jest funkcją przyrostów temteratury i ciśnienia względem podanych wartości
wzorcowych (E.Osada: Wykłady z geodezji i geoinformatyki 2 Tachimetria).

8

1.3. Bł

ę

dy przypadkowe

Bł

ę

dy przypadkowe

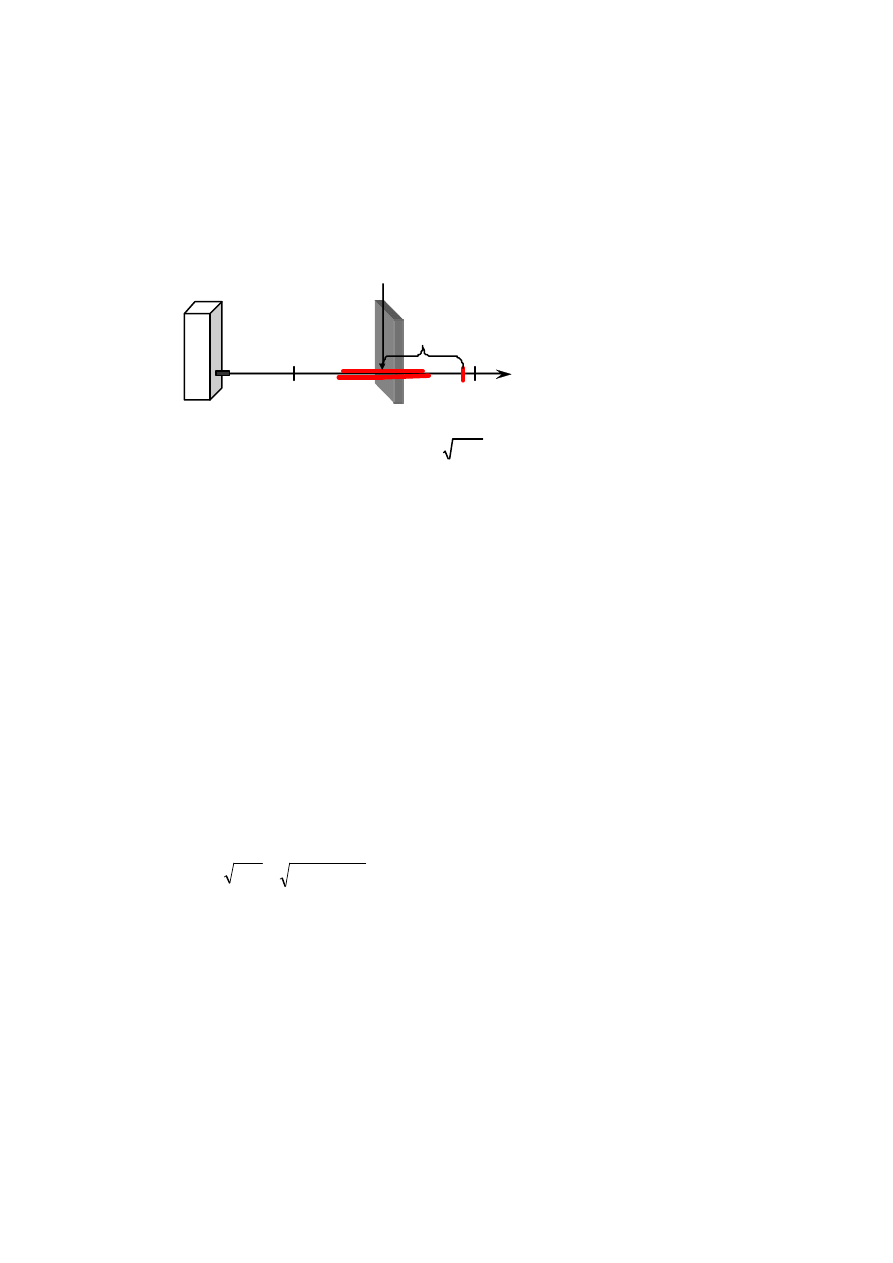
Z doświadczenia wiadomo, że wynik pomiaru pewnej wielkości x przyjmuje wartość
z przedziału a < x < b którego wielkość zależy od dokładności użytego przyrządu
pomiarowego (rys. 1.3.1).

v = x – Ex – odchylenie x (przyjmuje wartości
dodatnie i ujemne, Ev= 0 )

x - wynik pomiaru (zmienna losowa)

- odchylenie standardowe

2

Ev

=

σ

a

b

DISTO

m

m

Ex - wartość średnia

t

t

t = E

|

v

|

- odchylenie przeciętne

Rys. 1.3.1

Wynik pomiaru jest więc zmienną losową o wartości średniej Ex znajdującej się
w pobliżu środka przedziału (a, b).
Odchylenie wyniku pomiaru od wartości średniej v = x

−

Ex , nazywane błędem

przypadkowym pomiaru przyjmuje wartości dodatnie i ujemne, stąd jego wartość
ś

rednia jest równa zero Ev = 0.

Bł

ą

d przeci

ę

tny, bł

ą

d

ś

redni, wariancja

Miarami zmienności (rozrzutu) wyniku pomiaru x wokół wartości średniej Ex są:

wartość średnia bezwzględnej wartości odchylenia wyniku pomiaru, nazywana

•

odchyleniem przeciętnym:

t = E

|

v

|

pierwiastek z wartości średniej kwadratu odchylenia wyniku pomiaru, nazywany

•

odchyleniem średniokwadratowym, standardowym lub błędem średnim
pojedynczego pomiaru:

2

2

)

(

E

E

Ex

x

v

−

=

=

σ

kwadrat odchylenia standardowego nazywany wariancją:

•

σ

2

= Ev

2

= E(x-Ex)

2

9

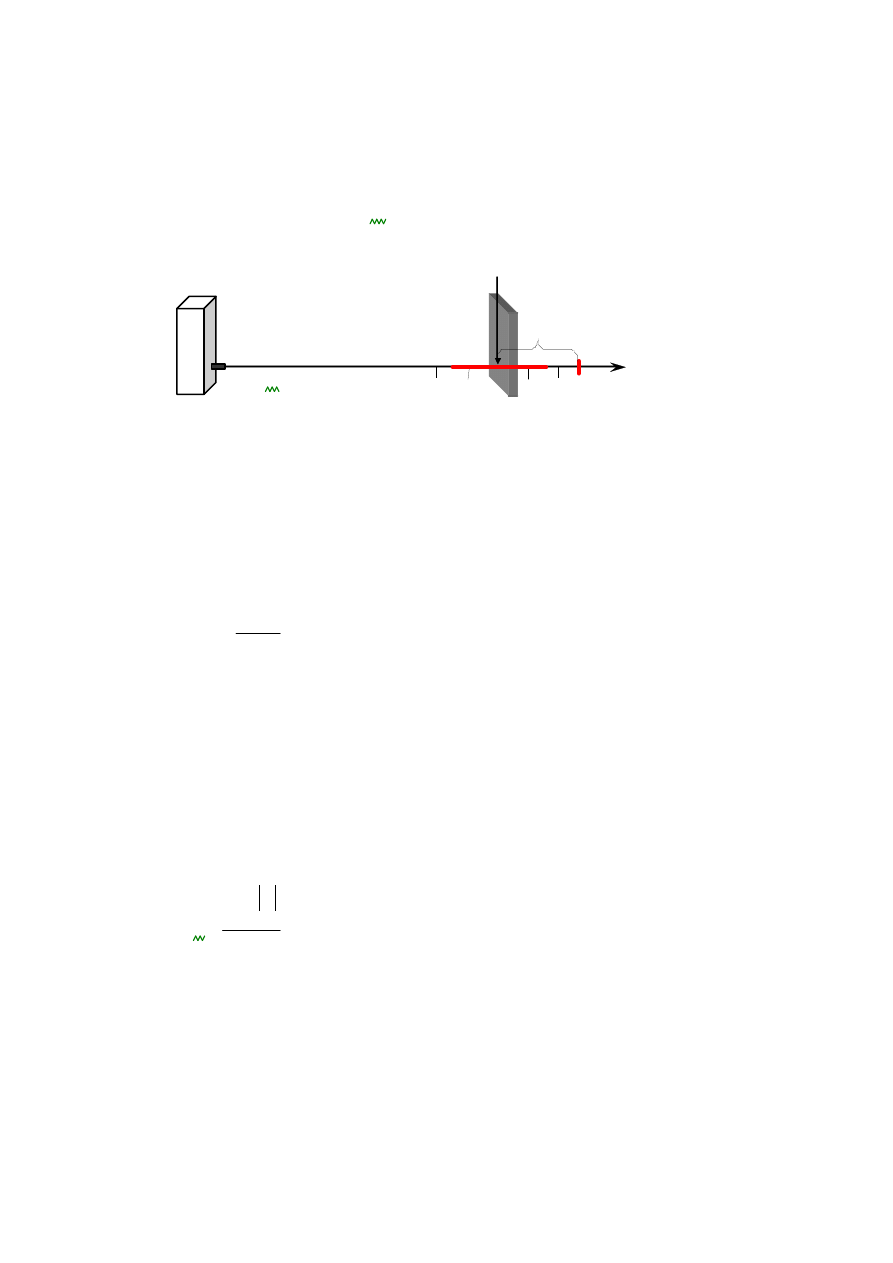
1.4. Warto

ść

ś

rednia

Ś

rednia arytmetyczna

Dane są wartości wyników pomiarów jednakowo dokładnych x

i

, i = 1,2,...n o błędzie

ś

rednim pojedynczego pomiaru

m

0.002

:=

(rys. 1.4.1).

v

i

= x

i

– x

s r

– błąd przypadkowy

x

sr

- wartość średnia

x

i

– wyniki pomiarów

x

2

x

3

x

4

x

1

DISTO

m

sr

m

sr

sr

sr

sr

sr

x

x

v

x

x

v

x

x

v

x

x

v

−

=

−

=

−

=

−

=

4

4

3

3

2

2

1

1

x

4.006

4.002

4.008

4.004





















:=

n

4

:=

i

1 n

..

:=

Rys. 1.4.1

Wartość średnia x

sr

jest wyznaczana w wyniku minimalizacji sumy kwadratów błędów

przypadkowych v

i

= x

i

−

x

sr

:

Σ

v

i

2

= v

1

2

+ v

2

2

+..+ v

n

2

= min.

Warunek konieczny minimum przyjmuje postać

Σ

v

i

= v

1

+ v

2

+..+ v

n

= 0, skąd

poszukiwana wartość średnia jest dana wzorem średniej arytmetrycznej:

xsr

1

n

i

x

i

∑

=

n

4.005

=

:=

Otrzymane błędy przypadkowe

v

x

xsr

−

:=

:

v

1

0.001

=

v

2

0.003

−

=

v

3

0.003

=

v

4

0.001

−

=

spełniają warunek Ev = 0:

1

n

i

v

i

∑

=

0

=

Błąd przeciętny pojedynczego pomiaru wynosi

t

1

n

i

v

i

∑

=

n

0.0020

=

:=

10

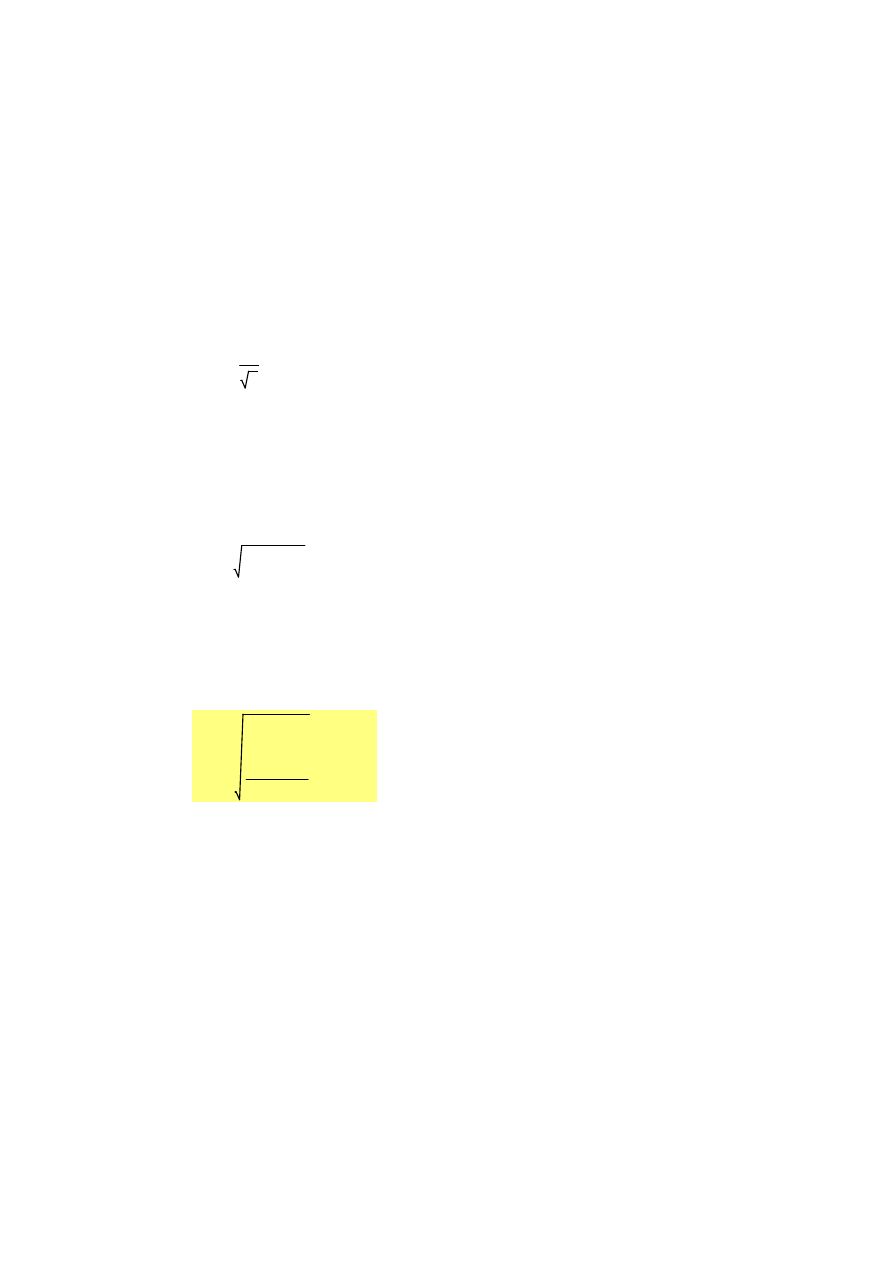
Pomiary były wykonane tym samym przyrządem w sposób niezależny, zatem:

wariancje wyników pomiarów są jednakowe

m

i

2

= Ev

i

2

= m

2

, natomiast

•

kowariancje m

ij

= Ev

i

v

j

, i

≠

j = 1,2,...n - wyrażające zależności między

•

poszczególnymi pomiarami, są z założenia równe zero: m

ij

= Ev

i

v

j

= 0.

Ś

rednia arytmetyczna x

ś

r

jako funkcja wyników pomiarów jest zmienną losową

o wariancji:

m

ś

r

2

= E(x

ś

r

- Ex

ś

r

)

2

= E(v

1

+...+v

n

)

2

/n

2

≡

(Ev

1

2

+...+Ev

n

2

)/n

2

= m

2

/n.

Stąd, błąd średni średniej arytmetycznej dany jest wzorem:

msr

m

n

0.0010

=

:=

Podobnie, odchyłki jako funkcje wyników pomiarów v

i

= x

i

−

x

ś

r

są zmiennymi

losowymi o wariancjach:

m

vi

2

= E(x

i

- x

ś

r

)

2

= E(x

i

- x

ś

r

+ Ex - Ex)

2

= E(v

i

- (v

1

+...+v

n

)/n)

2

= m

2

- m

ś

r

2

.

Zatem, błędy średnie odchyłek są jednakowe i równe:

mv

m

2

msr

2

−

0.0017

=

:=

Wartość średnia sumy kwadratów odchyłek jest równa:

EΣv

i

2

= EΣ(x

i

- x

ś

r

)

2

= EΣ[v

i

- (v

1

+...+v

n

)/n]

2

= m

2

(n - 1)

Stąd, błąd średni pojedynczego pomiaru wynosi:

m0

1

n

i

v

i

( )

2

∑

=

n

1

−

0.0026

=

:=

Jeżeli obliczona wartość błędu pojedynczego pomiaru jest w przybliżeniu równa

wartości znanej

m0 0.0026

=

≈

m

0.002

=

- podanej przez producenta przyrządu

pomiarowego to wyniki pomiarów są zgodne. W tym przypadku wartość średnia i jej
błąd średni x

ś

r

±

m

ś

r

są poprawne, a ochyłki v zawierają się na ogół, co do bezwzględnej

wartości w przedziale 2 - 3 krotnego ich błędu średniego:

|

v

| ≤

2 mv

⋅

0.0035

=

.

11

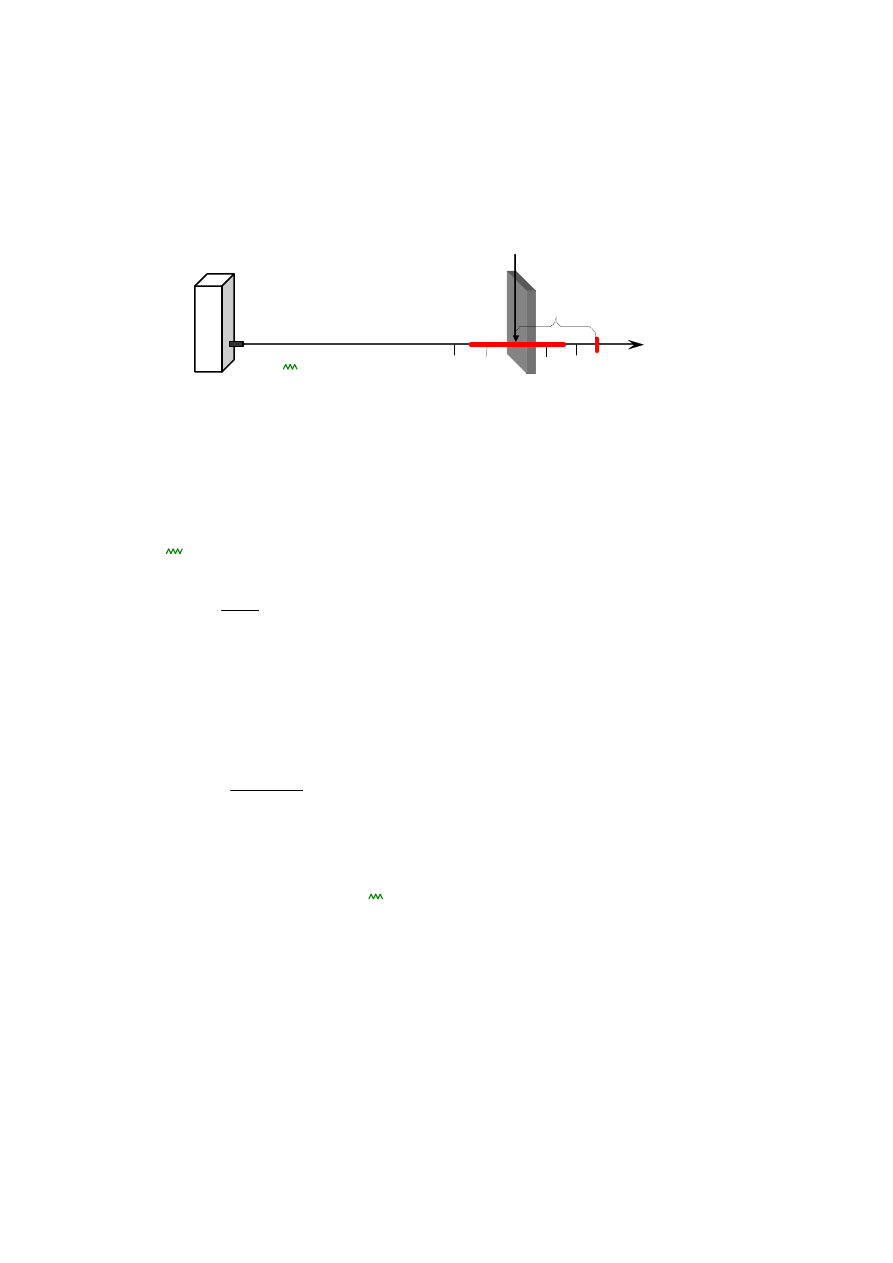
1.5.

Ś

rednia wa

ż

ona

Ś

rednia arytmetyczna wa

ż

ona

Dane są wyniki niejednakowo-dokładnych pomiarów x

i

±

m

i

, i = 1,2,...n (rys.1.5.1).

v

i

= x

i

– x

s r

– błąd przypadkowy

x

i

– wyniki pomiarów

x

2

x

3

x

4

x

1

DISTO

m

sr

m

sr

x

sr

- wartość średnia

x

4.006

4.002

4.008

4.004





















:=

m

0.002

0.003

0.002

0.004





















:=

n

4

:=

i

1 n

..

:=

Rys. 1.5.1.

Wartość średnia wyników pomiarów x

sr

jest wyznaczana ważoną metodą najmniejszych

kwadratów

Σ

p

i

v

i

2

= p

1

v

1

2

+ p

2

v

2

2

+..+ p

n

v

n

2

= min.

Jako wagi przyjmuje się liczby odwrotnie proporcjonalne do kwadratów błędów

ś

rednich pomiarów p

i

= m

2

/ m

i

2

gdzie współczynnik m jest równy jedności m = 1 lub

równy błędowi obserwacji której waga będzie równa jedności, na przykład pierwszej

m

m

1

:=

:

p

i

m

2

m

i









2

:=

p

1.00

0.44

1.00

0.25





















=

Warunek konieczny minimum p

1

v

1

+ p

2

v

2

+..+ p

n

v

n

= 0 prowadzi do wzoru średniej

arytmetycznej ważonej:

x.sr

1

n

i

p

i

x

i

⋅

( )

∑

=

1

n

i

p

i

∑

=

4.006

=

:=

Otrzymane błędy przypadkowe

v

x

x.sr

−

:=

:

v

1

0.0001

=

v

2

0.0039

−

=

v

3

0.0021

=

v

4

0.0019

−

=

12

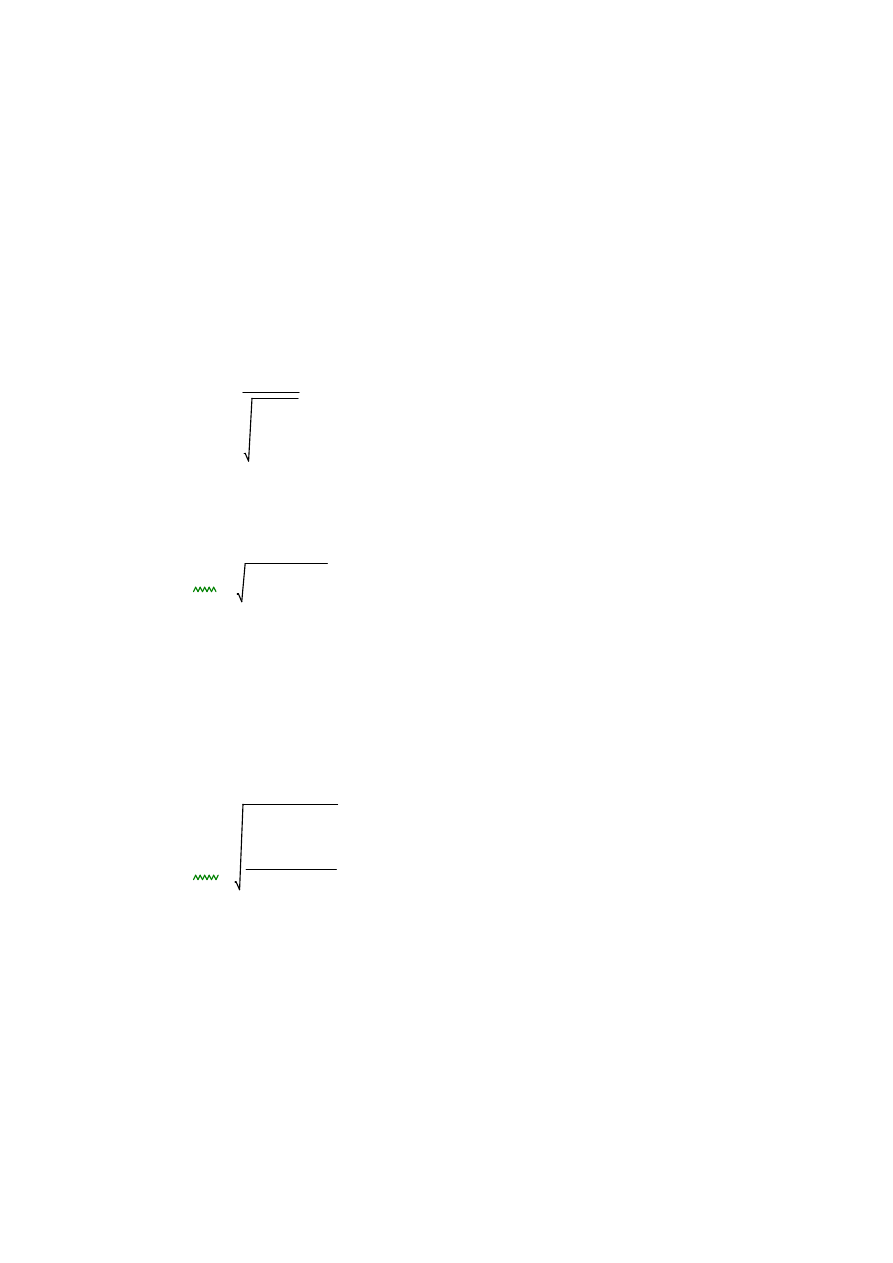
spełniają warunek konieczny minimum Ep

i

v

i

= 0

1

n

i

p

i

v

i

⋅

( )

∑

=

0.000

=

Pomiary są różnej dokładności więc:

wariancje wyników pomiarów nie są jednakowe m

i

2

= Ev

i

2

, natomiast

•

kowariancje m

ij

= Ev

i

v

j

, i

≠

j = 1,2,...n - wyrażające zależności między

•

poszczególnymi pomiarami, są z założenia równe zero: m

ij

= Ev

i

v

j

= 0.

Ś

rednia arytmetyczna ważona x

ś

r

jako funkcja wyników pomiarów jest zmienną

losową o wariancji m

ś

r

2

= E(x

ś

r

−

Ex

ś

r

)

2

= E(

Σ

p

i

v

i

)

2

/(

Σ

p

i

)

2

= m

2

/

Σ

p

i

.

Stąd, błąd średni średniej arytmetycznej ważonej dany jest wzorem:

m.sr

m

1

n

i

p

i

∑

=

0.0012

=

:=

Podobnie, odchyłki jako funkcje wyników pomiarów v

i

= x

i

−

x

ś

r

są zmiennymi losowymi

o wariancjach m

vi

2

= E(x

i

−

x

ś

r

)

2

= E(x

i

−

x

ś

r

+ Ex

−

Ex)

2

= E(v

i

−

(v

1

+...+v

n

)/n)

2

= m

i

2

- m

ś

r

2

. Zatem, błędy średnie odchyłek wynoszą:

mv

i

m

i









2

msr

2

−

:=

mv

0.0017

0.0028

0.0017

0.0039





















=

Wartość oczekiwana (średnia) ważonej sumy kwadratów odchyłek jest równa

E

Σ

p

i

v

i

2

= E

Σ

p

i

(x

i

−

x

ś

r

)

2

= E

Σ

[v

i

−

(v

1

+...+v

n

)/n]

2

= m

2

(n

−

1).

Otrzymana stąd wartość współczynnika m:

m0

1

n

i

p

i

v

i

( )

2

⋅









∑

=

n

1

−

0.00201

=

:=

powinna być równa z dokładnością do 10% wartości przyjętej do wagowania

m

0.0020

=

.

13

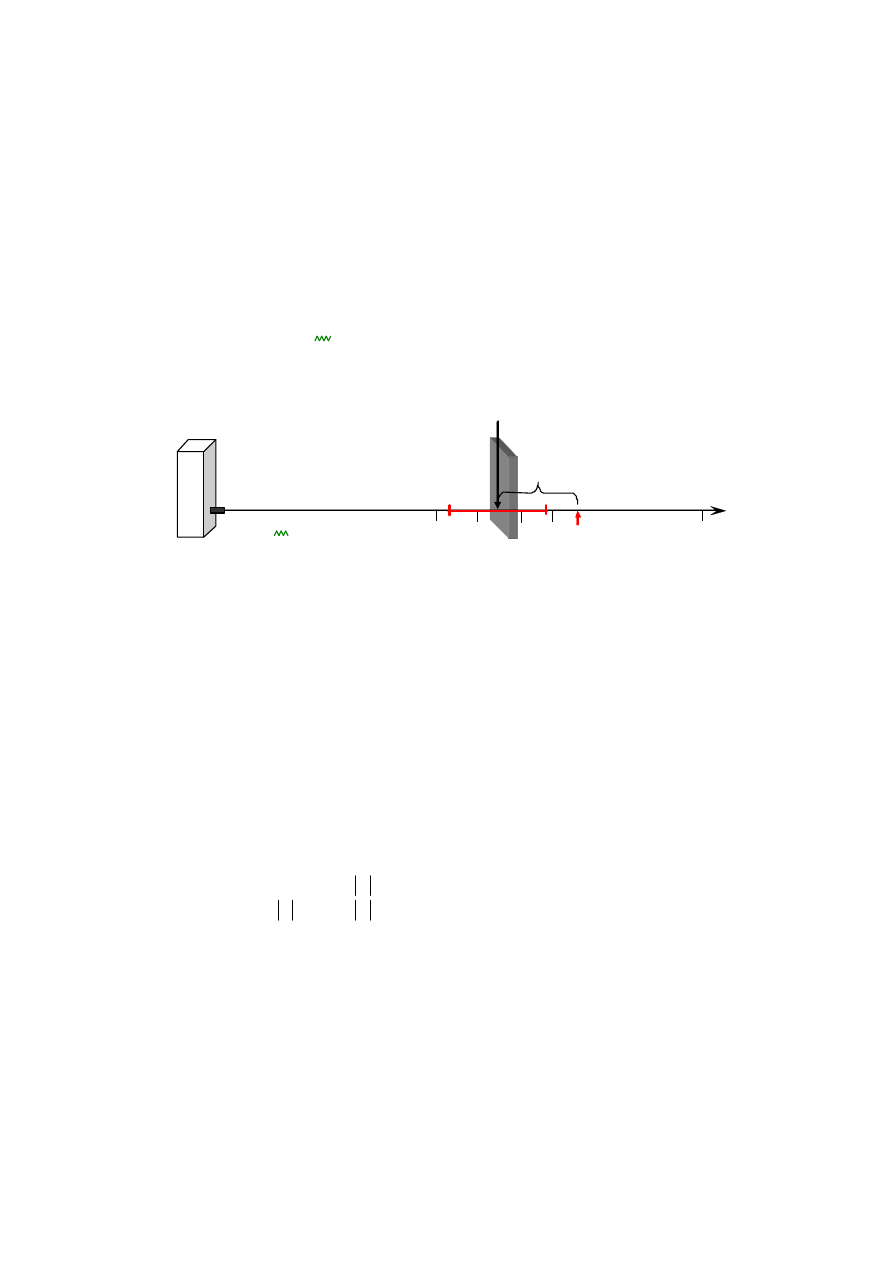
v = x – Ex – błąd przypadkowy
wyniku pomiaru

x – wynik pomiaru

x

2

x

3

x

4

x

1

DISTO

m

m

Ex - wartość oczekiwana
wyniku pomiaru

x

sr

x

5

Zatem, w przypadku m

0

≈

m wyniki pomiarów są zgodne, otrzymana wartość średnia

i jej błąd średni x

ś

r

±

m

ś

r

są poprawne, a odchyłki v zawierają się na ogół, co do

bezwzględnej wartości w przedziale 2 - 3 krotnego ich błędu średniego

|

v

i

| ≤

2m

vi

.

1.6.

Ś

rednia odporna

Ś

rednia odporna na obserwacje odstaj

ą

ce

Dane są wartości wyników pomiaru odległości x

1

, x

2

,.. x

5

dalmierzem o błędzie średnim

pojedynczego pomiaru

m

0.0025

:=

m (rys. 1.6.1). Obserwacja x

5

wyraźnie odstaje od

pozostałych, jest obciążona błędem grubym (rys. 1.6.1).

x

4.006

4.002

4.008

4.004

4.040





























:=

n

5

:=

i

1 n

..

:=

Rys. 1.6.1.

W takich przypadkach, po obliczeniu wartości średniej poprawki obserwacji
odstających v będą miały duże wartości, warunek

|

v

| ≤

3m

v

nie będzie spełniony przez te

obserwacje. Obliczenia wartości średniej są kontunuowane odrzucając za każdym razem
obserwację odstającą o największej wartości poprawki v aż do spełnienia kryterium

|

v

| ≤

3m

v

przez pozostałe obserwacje.

Inny sposób polega na iteracyjnym obliczaniu średniej ważonej, przypisując na każdym
kroku obserwacjom odstającym coraz to mniejsze wagi, w zależności od ich rosnących
odchyłek v. W ten sposób ich wpływ na wyznaczaną wartość średnią jest
minimalizowany - tak jakby były odrzucane. Można to osiągnąć na różne sposoby, na
przykład przez powiększanie błędów obserwcji odstających m

i

dla których

|

v

i

| >

3m

i

,

o ich odległość od granicy przedziału ufności:

|

v

i

|

- 3m

i

. W tym przypadku modyfikacja

błędów średnich wszystkich obserwacji następuje na każdym koroku iteracji według
zależności:







>

−

+

≤

=

i

i

i

i

i

i

i

i

i

m

v

m

v

m

m

v

m

m

3

)

3

(

3

natomiast wag:

14