Postanowiono sprawdzić w jakim stopniu wydajność pracy robotników zatrudnionych na określonym stanowisku pracy zależy od czasu ich szkolenia
i od stażu pracy.
W tym celu zebrano dane o 14 osobach:
Wydajność pracy w szt./godz. |
Czas szkolenia w miesiącach |
Staż pracy w latach |
Y |
X1 |
X2 |
13 |
3 |
5 |
11 |
2 |
4 |
10 |
1 |
5 |
8 |
0 |
1 |
7 |
1 |
0 |
8 |
2 |
0 |
9 |
0 |
2 |
11 |
2 |
3 |
10 |
3 |
3 |
9 |
1 |
2 |
11 |
2 |
4 |
11 |
2 |
5 |
10 |
1 |
2 |
12 |
2 |
2 |
Jaki jest łączny wpływ czasu szkolenia i stażu pracy na wydajność pracy robotników?
W celu ustalenia odpowiedzi na to pytanie musimy wyliczyć współczynnik korelacji wielorakiej R:
![]()
Liczymy w tym celu współczynniki korelacji między wszystkimi parami zmiennych:
|
Y |
X1 |
X2 |
Y |
1 |
|
|
X1 |
0,6409 |
1 |
|
X2 |
0,7754 |
0,4406 |
1 |
Następnie liczymy współczynnik korelacji cząstkowej ![]()
:
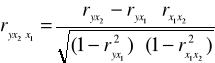
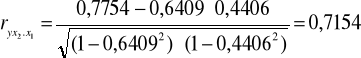
Ostatecznie otrzymujemy:
![]()
Wyznacz funkcję regresji wydajności pracy względem czasu szkolenia i stażu pracy:
![]()
|
Wydajność pracy w szt./godz. |
Czas szkolenia w miesiącach |
Staż pracy w latach |
|
Y |
X1 |
X2 |
|
13 |
3 |
5 |
|
11 |
2 |
4 |
|
10 |
1 |
5 |
|
8 |
0 |
1 |
|
7 |
1 |
0 |
|
8 |
2 |
0 |
|
9 |
0 |
2 |
|
11 |
2 |
3 |
|
10 |
3 |
3 |
|
9 |
1 |
2 |
|
11 |
2 |
4 |
|
11 |
2 |
5 |
|
10 |
1 |
2 |
|
12 |
2 |
2 |
średnia |
10 |
1,57 |
2,71 |
odch. stand. |
1,60 |
0,90 |
1,67 |
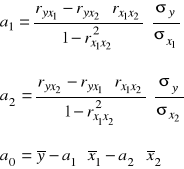
0,59 |
0,66 |
7,37 |
0,17 |
0,32 |
0,58 |
0,7123 |
0,9703 |
#N/D! |
13,6192 |
11 |
#N/D! |
25,6439 |
10,3561 |
#N/D! |
Funkcja regresji ma postać:
![]()
![]()
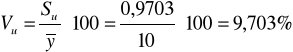
Miernikiem określającym typowe zmiany zmiennej wywołane typową zmianą zmiennej Xi jest tzw. współczynnik beta:
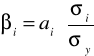
W naszym zadaniu otrzymamy:
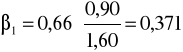
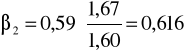
Wyszukiwarka
Podobne podstrony:
2Funkcja regresji w przypadku trzech zmiennych, Statystyka opisowa
ELEMENTY STATYSTYKI OPISOWEJ - SCENARIUSZ, Matematyka dla Szkoły Podstawowej, Gimnazjum
Zmienna losowa, Statystyka opisowa i matematyczna, Statystyka opisowa i matematyczna, Statystyka opi
Indeksy agregatowe dla wielkości absolutnych, Statystyka opisowa
Regresja liniowa dwoch zmiennych, materiały z roku 2011-2012, Semestr II, Statystyka opisowa - ćwicz
Wykłady ze statystyki opisowej dla psychologów
Statystyka opisowa w Excelu dla szkol cwiczenia praktyczne
Statystyka opisowa w Excelu dla szkol cwiczenia praktyczne cwstex
Statystyka opisowa w Excelu dla szkol cwiczenia praktyczne 2
Statystyka opisowa w Excelu dla szkol cwiczenia praktyczne cwstex
STATYSTYKA OPISOWA '
1 Statystyka opisowa Wprowadze Nieznany (2)
Gorgol I Elementy statystyki opisowej
więcej podobnych podstron