Obliczenia

Obliczenie Us ,  i 

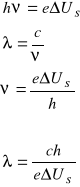
c = 2,898 10⁸ [m/s]

h = 6,626 10^-34 [Js]

e = 1,602 10^-19 [C]

Wartość U_S określamy jako średnią różnicę dwóch kolejnych napięć:

Wartość  i  obliczamy dla każdego napięcia anodowego jako:

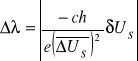
gdzie δU_S = 0,2 V

Ua	Us1		Us2		Us3		Us4		Us5		 	 
0,5	6,0	8,0	10,5	3,0	14,5	5,8	20,3	5,8	-	-	2164,68	75,69
1,00	7,1	3,8	10,8	5,7	15,6	5,7	20,7	5,7	26	5,8	2137,43	74,33
1,50	7,1	4,8	10,8	5,2	15,6	6,1	20,6	6,2	25,5	6,3	2103,57	69,37
2.0	7,1	4,8	11,1	5,3	15,4	5,9	20,4	6,2	26,5	6,4	2098,7	68,87

Obliczam wartość średnią Ea_i:

Lp	Us [V]	Eai = Us [eV]
1	5,6	5,6
2	5,6	5,6
3	5,8	5,8
	Średnia:	5,67

Ea_śr = 5,67 [eV]

Obliczam odchylenie standardowe S_Ea:

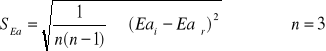
S_Ea = 0,13 [eV]

Test równości wartości średnich: Ea₀=5,1

H₀ : Ea_śr = Ea₀

H_A : Ea_śr < Ea₀

Wartość krytyczną odczytujemy z tablic Studenta uwzględniając liczbę stopni swobody r=2 i wartość poziomu ufności 0,95.

t= 3,9

nie ma podstaw do odrzucenia H₀

 = 2126,096 ± 72,065 [Å]

eU = 5,67 ± 0,13[eV]

Hipoteza zerowa: H₀ :
= μ

Hipoteza alternatywna: H₁ :
< μ

Ustalam poziom ufności na α = 0,01

Przyjmuje zmienną losową standaryzowaną:

σ - odchylenie standardowe z populacji:

n - liczba pomiarów (n = 3)

Jeżeli wynik u < - u_α to hipotezę zerową należy odrzucić.

Jeżeli -u_α ≤ u ≤ u_α to hipotezę zerową należy przyjąć.

Jeżeli u ≥ - u_2α to należy przyjąć hipotezę zerową.

Wartość u_α odczytuję z tablic dystrybuanty rozkładu normalnego, a wartość u_2α z tablic rozkładu Studenta dla r = ∞.

1. σ = 0,786

u = 0,1056 ≈ 0,1

u_α = 0,54

-0,54 ≤ u ≤ 0,54

W związku z tym przyjmuję hipotezę zerową. Wartość średnia tej serii pomiarowej jest równa wartości rzeczywistej.

2. σ = 0,845

u = 0,196 ≈ 0,2

u_α = 0,583

-0,583 ≤ u ≤ 0,583

W związku z tym przyjmuję hipotezę zerową. Wartość średnia tej serii pomiarowej jest równa wartości rzeczywistej.

3. σ = 0,126

u = 7,464

u_2α = 2,858

u ≥ - u_2α

W związku z tym nie ma podstaw, aby odrzucić hipotezę zerową. Wartość średnia tej serii pomiarowej jest równa wartości rzeczywistej.

4. σ = 0,081

u = 9,045

u_2α = 2,858

u ≥ - u_2α

W związku z tym nie ma podstaw, aby odrzucić hipotezę zerową. Wartość średnia tej serii pomiarowej jest równa wartości rzeczywistej.

WNIOSKI.

Wyniki, jakie otrzymałem w pomiarach pozwoliły na wyliczenie czterech różnych wartości długości emitowanej fali. Analizę otrzymanych wyników przeprowadziłem za pomocą testu równości wartości średnich. We wszystkich seriach pomiarowych otrzymałem wyniki zbliżone do wartości 2,341∙10^-7 m, jest to długość fali emitowanej przez atomy rtęci wzbudzone zderzeniami z elektronami wg. książki „Kurs fizyki” B. Jaworskiego i A. Dietłafa. Po wyliczeniu okazało się także, że nie wystąpiły podstawy do odrzucenia hipotezy zerowej, co oznacza, że otrzymane wartości mogą stanowić wartość rzeczywistą.

Rozbieżności w wartościach otrzymanych długości fali nie są duże. Niewielkie różnice mogą być spowodowane niedokładnymi pomiarami. Aparatura, na której wykonywane są pomiary jest dość stara i zużyta, co może powodować pojawianie się niewielkich błędów. Można tego uniknąć używając nowocześniejszego i dokładniejszego sprzętu pomiarowego lub też dokonując większej ilości pomiarów.

---