Wojewódzki Konkurs Matematyczny

Marzec 2006

Uczniu!

Przed Tobą 16 zadań zamkniętych, za które możesz uzyskać 16 punktów oraz 4 zadania otwarte - każde za 6 punktów.

W zadaniach zamkniętych zakreśl kółkiem na arkuszu dokładnie jedną poprawną odpowiedź, w przypadku pomyłki skreśl krzyżykiem błędną odpowiedź i ponownie zakreśl kółkiem właściwą.

W zadaniach  otwartych przedstaw starannie swoje rozwiązanie. W tym celu wykonaj rysunki pomocnicze (o ile to konieczne), zadbaj o właściwe oznaczenia, zamieść niezbędne wyjaśnienia i zaprezentuj cały tok rozwiązania w wyznaczonym miejscu arkusza.

Na rozwiązanie zestawu masz 90 minut. To dużo czasu.

Życzymy Ci powodzenia.

1. Jestem liczbą. Liczba moich setek jest podwojeniem cyfry moich jedności, która jest potrojeniem cyfry moich dziesiątek. Cyfra moich dziesiątek wynosi 3. Kim jestem?

A. 1839 B. 1236 C. 231 D. 9381

2. Kamil musi wykonać działanie
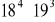
   . Jaka jest ostatnia cyfra wyniku?

A. 2 B. 8 C. 4 D. 9

3. Dwaj chłopcy mierzyli długość mostu krokami. Długość kroku Heńka wynosiła 60cm, a Pawła 70cm. Jaką długość ma most, jeżeli ślady stóp Pawła i Heńka pokryły się 9 razy?

A. 420cm B. 37,8m C. 11,7m D. 378cm

4. Kapitan ma na statku 31 marynarzy, których średnia wieku wynosi 23 lata. Jeżeli do obliczenia średniej wieku doliczymy wiek kapitana, to średnia wzrośnie do 24 lat. Ile lat ma kapitan?

A. 32 lata B. 45 lat C. 55 lat D. 25 lat

5. Jaką największą liczbę całkowitą można wpisać w kratkę, aby nierówność była prawdziwa?

1. 
   - 12

2. 11 - 10,01 - > 0

3. - 10

4. - 11

6. Jaś ma zamiar kupić drukarkę laserową, uzbierał na nią 1584zł, a od mamy dostał 16% kwoty potrzebnej na ten zakup. Teraz ma na nią 61% potrzebnej kwoty. Ile kosztuje ta drukarka laserowa?

A. 2297zł B. 2597zł C. 2550zł D. 3520zł

7. Stary podręcznik do algebry leżał wiele lat na strychu i niektóre jego fragmenty zostały zjedzone przez myszy. Jakie wyrażenie algebraiczne zjadły myszy?

1. 
   - x + 7y

2. 
   x - 7y

3. x + 7y

4. - x - 7y

8. ,,31% pewnej liczby jest o 4 większe od 11% tej liczby.” Które równanie pozwoli mi wyznaczyć szukaną liczbę?

1. 31% a = 11% a + 4 C. 31% a =
   a

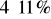
2. 31% a + 4 = 11% a D.
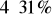
   a = 11% a

9. Końce podstawy trójkąta równoramiennego mają współrzędne (2,1) i (6,1). Pole trójkąta wynosi 10 j
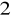
   . Jakie współrzędne może mieć trzeci wierzchołek tego trójkąta?

A. (2, -4) B. (5, -4) C. (4, -4) D. (6, -4)

10. Na planie w skali 1: 2500 pewien teren ma kształt prostokąta o wymiarach 64mm x 48mm. Jaka jest rzeczywista powierzchnia tego terenu?

A. 192 m
B. 1,92 ha C. 768 ha D. 7,68 ha

11. 
    Na rysunku ABCD jest kwadratem, zaś ABE trójkątem równobocznym. Jaka jest miara kąta DEC?

1. 60
   

2. 120
   

3. 90
   

4. 150
   

12. 
    Na rysunku przedstawione są trzy okręgi. Promienie tych okręgów mają długości 9 cm, 4 cm, 3 cm. Jaki obwód ma trójkąt ABC?

1. 16 cm

2. 18 cm

3. 20 cm

4. 23 cm

13. Ile jest liczb od 1 do 100, których zapis w systemie rzymskim ma dwie osie symetrii?

A. 7 B. 6 C. 4 D. 2

14. Jeśli z przedstawionej na rysunku siatki skleisz sześcian, to jaka litera znajdzie się na ścianie przeciwległej do tej, na której jest litera F?

1. 
   A

2. B

3. C

4. D

15. W pewnym graniastosłupie jest dwa razy więcej krawędzi niż ścian. Jaka figura jest podstawą tego graniastosłupa?

A. trójkąt B. czworokąt C. pięciokąt D. sześciokąt

16. Która zależność nie może się zdarzyć?

1. wysokość ostrosłupa jest równa jednej z krawędzi bocznych

2. wysokość ostrosłupa jest mniejsza niż krawędź boczna

3. wysokość ostrosłupa jest większa niż jedna z krawędzi bocznych

4. wysokość ostrosłupa jest równa wysokości jednej ze ścian bocznych

Zadanie I

Kasia ma 10 lat, a jej brat Michał jest o osiem lat starszy. Ojciec Kasi i Michała ma 45 lat. Za ile lat ojciec będzie miał tyle lat, co jego dzieci razem?

Zadanie II

Do zbiornika w kształcie prostopadłościanu o wymiarach 20 dm, 10 dm i 10 m wlano 5000 litrów mleka o zawartości 3,4% tłuszczu. Resztę dopełniono mlekiem o zawartości tłuszczu 4,2%. Ile procent tłuszczu zawiera obecnie mleko w zbiorniku?

Zadanie III

Pewnego dnia na bazarze sprzedawczyni jajek sprzedała pierwszemu klientowi połowę jajek, które miała w koszyku, i jedno. Drugiemu klientowi sprzedała połowę tego, co zostało, i jedno. Trzeci kupił połowę z tego, co zostało, i jedno jajko. Dla czwartego klienta zostało jedno jajko. Ile jajek było w koszyku? Ile jajek kupił pierwszy, ile drugi, a ile trzeci klient?

Zadanie IV

Dany jest ostrosłup czworokątny ABCDS, gdzie S to wierzchołek ostrosłupa. Podstawą ostrosłupa jest prostokąt ABCD, w którym przekątne o długości 12 cm przecinają się pod kątem 60
.Obwód podstawy wynosi 32,8 cm. Trójkąt ACS, zawierający wysokość ostrosłupa jest trójkątem równoramiennym prostokątnym. Jaką objętość ma ten ostrosłup?

4

4(2x - 3y) - 2(5x + ) = - 4x + 2y

A

B

C

D

F

E

A

B

D

C

E

A

B

C

---