Rozkładem ![]()
z k - stopniami swobody nazywamy rozkład następującej sumy:
![]()
gdzie x1, aż do xk są niezależnymi zmiennymi losowymi o rozkładzie normalnym N(0,1). Ponadto wartość oczekiwana jest równa![]()
, a wariancja ![]()
Rozkładem t - Studenta z k - stopniami swobody nazywamy rozkład prawdopodobieństwa zmiennej losowej Tk określonej następująco:
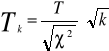
, gdzie ![]()
i ![]()
są niezależnymi zmiennymi losowymi. T ma rozkład normalny N(0,1), zaś zmienna ![]()
ma rozkład ![]()
z k - stopniami swobody. Ponadto wartość oczekiwana tego rozkładu jest równa ![]()
, a wariancja ![]()
Czas obsługi w kasie studenckiej jest zmienną o rozkładzie T-Studenta z 60 stopniami swobody. Jakie jest prawdopodobieństwo, że losowo wybrany student będzie obsługiwany przy kasie dłużej niż dwie minuty?
Przy sprawdzaniu prawdziwości pewnej opinii zastosowano zmienną losową o rozkładzie chi-kwadrat o 5 stopniach swobody. Przyjęto założenie, że opinia jest fałszywa, jeśli wartość tej zmiennej wyniesie, co najmniej 20,515.. Określ prawdopodobieństwo ocenianej opinii.
Niech zmienna losowa
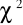
ma rozkład chi-kwadrat z 13 stopniami swobody. Znaleźć prawdopodobieństwo:
![]()
![]()
![]()
Niech zmienna losowa
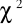
ma rozkład chi-kwadrat z 24 stopniami swobody. Znaleźć prawdopodobieństwo:
![]()
![]()
![]()
Niech zmienna losowa T ma rozkład T-Studenta z 40 stopniami swobody. Znaleźć prawdopodobieństwo:
![]()
![]()
![]()
Niech zmienna losowa T ma rozkład T-Studenta z 28 stopniami swobody. Znaleźć prawdopodobieństwo:
![]()
![]()
![]()
![]()
Elementy teorii estymacji - przedział ufności dla średniej.
Model I.
Populacja generalna ma rozkład normalny ![]()
. Wartość średnia m jest nieznana, a odchylenie standardowe ![]()
jest znane w populacji. Przy takich założeniach wylosowano próbę o liczebności n - elementów wylosowanych niezależnie.
Wzór na przedział ufności dla średniej m populacji jest następujący:
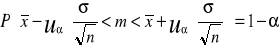
![]()
- średnia arytmetyczna obliczona z wyników próby
![]()
- jest prawdopodobieństwem przyjętym i nazywanym współczynnikiem (poziomem) ufności.
![]()
- wartości zmiennej losowej u mającej rozkład normalny standaryzowany
Model II (n<=30)
Populacja generalna ma rozkład ![]()
, a wartość średniej jest nieznana jak i też odchylenie standardowe.
Z populacji wylosowano niezależnie małą próbę o liczebności n - elementów.
Wzór na przedział ufności dla średniej m populacji jest następujący:
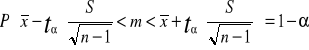
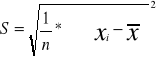
![]()
- jest wartością zmiennej t, t - Studenta odczytaną z tablicy tego rozkładu dla n-1 stopni swobody.
Model III (n>120)
Populacja generalna ma rozkład normalny lub dowolny inny o średniej m i skończonej nieznanej wariancji równej ![]()
. Z populacji wylosowano próbę o dużej liczebności n elementów wylosowanych niezależnie, przy czym liczebność próby jest duża.
Wzór na przedział ufności dla średniej:
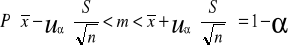
Dla oszacowania średniego stażu pracy pracowników pewnej firmy, wylosowano 12 osób, dla których odchylenie standardowe stażu pracy wynosi s= 5 lat a średnia arytmetyczna jest równa 8,4. Zakładając, że rozkład stażu jest normalny, oszacować średni staż pracy pracowników tej firmy. Przyjąć współczynnik ufności l - α = 0,9.
W pewnym eksperymencie chemicznym bada się ilość czystej substancji wydzielającej się w toku doświadczenia. Przeprowadzono n=20 niezależnych doświadczeń i otrzymano w nich następujące wyniki (w mg):
Z pewnej populacji o rozkładzie normalnym
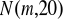
wylosowano 16-elementową próbę prostą otrzymując z niej średnią równą 60. Należy podać przedziałowe oszacowanie nieznanej średniej wartości m populacji, przyjmując współczynnik ufności równy 0,99.W celu sprawdzenia średnich zarobków w pewnej firmie pobrano losowo próbkę 200. pracowników i otrzymano średnie zarobki w wysokości 1000 złotych oraz odchylenie standardowe 200 złotych. Na poziomie ufności 0,95 oszacuj metodą przedziałową średnie zarobki w tej firmie.
343 |
308 |
342 |
387 |
257 |
293 |
359 |
348 |
383 |
385 |
387 |
384 |
309 |
293 |
346 |
322 |
322 |
354 |
301 |
239 |
Przyjmując rozkład ilości wydzielonej substancji za normalny z odchyleniem standardowym 90 mg, oszacować za pomocą przedziału ufności ze współczynnikiem ufności 0,999 średnią ilość wydzielonej w tym doświadczeniu substancji.
Uwaga,
Najczęściej w zadaniach korzysta się z następujących wartości współczynników ufności: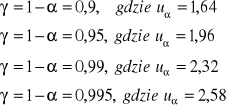
Metody prognozowania
Zestaw 1A
Wyszukiwarka
Podobne podstrony:
4428
4428
praca licencjacka b7 4428
4428
4428
4428
więcej podobnych podstron