f (x₁,x₂,x₃) = 2x₁² + 2x₂² + 3x₃² - 2x₁x₂ - 0.6667x₁x₃ + 1.3333x₂x₃ - 4x₁ - 4x₂ - 18x₃ + 37

Analityczne wyznaczenie minimum zadanej funkcji wielu zmiennych:

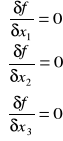
Rozwiązanie układu równań (za pomocą MATLABa):

X =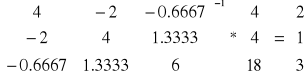

Rzeczywistym rozwiązaniem powyższego układu równań jest punkt (2,1,3)

Podstawiamy do hesjanu i obliczamy jego wyznacznik:

det(H) =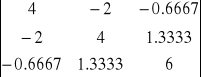
= 66.6669 > 0

Hesjan jest określony dodatnio, a więc punkt (2,1,3) jest minimum funkcji.

Wartość funkcji dla punktu(2,1,3):

f(2,1,3) = 4