∀ - dla każdego ∃ - istnieje
ZBIORY
Zbiór A⊂X nazywamy ograniczonym z góry (z dołu), jeżeli:
∃M∈X∀x∈A (x≤M),
∃m∈X∀x∈A (x≥m).
Zbiór A⊂X nazywamy ograniczonym, jeżeli jest ograniczony z dołu i z góry.
Kresem górnym (supremum) zbioru niepustego A⊂X nazywamy element K∈X taki, że:
∀x∈A (x≤K)
∀ε>0 ∃xo∈A (xo>K-ε)
Kresem dolnym (infinum) zbioru niepustego A⊂X nazywamy element k∈X taki, że:
∀x∈A (x≥k)
∀ε>0 ∃xo∈A (xo<k+ε)
FUNKCJE
Funkcją f:R→R nazywamy okresową jeżeli istnieje w∈R\{0} taka, że
f(x+w)=f(x) dla każdego x∈R.
Funkcję f:A⊂R→R nazywamy:
- parzystą, jeżeli ∀x,-x∈R zachodzi: f(−x)=f(x),
- nieparzystą, jeżeli ∀x,-x∈R zachodzi: f(−x)=−f(x).
CIĄGI
Każdą funkcję f:N→R nazywamy nieskończonym ciągiem liczb rzeczywistych
Ciąg (an) nazywamy:
rosnącym ⇔ ∀n∈N (an+1>an)
malejącym ⇔ ∀n∈N (an+1<an)
nierosnącym ⇔ ∀n∈N (an+1≤an)
niemalejącym ⇔ ∀n∈N (an+1≥an)
stałym ⇔ ∀n∈N (an=const)
Liczbę a∈R nazywamy granicą ciągu (an) jeżeli dla każdej liczby ε>0 istnieje liczba naturalna n∈N taka że nierówność |an-a|<ε jest spełniona dla wszystkich n>N.
![]()
Ciąg (an) nazywamy ograniczonym jeżeli ∃m,M∈R ∀n∈N zachodzi: (m≤an≤M)
Ciąg, który ma granicę nazywamy ciągiem zbieżnym. Pozostałe są rozbieżne:
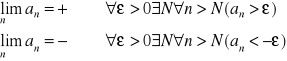
Własności ciągów zbieżnych
(o jednoznaczności granicy). Ciąg zbieżny nie może mieć dwóch różnych granic.
(warunek konieczny zbieżności). Każdy ciąg zbieżny jest ograniczony.
(warunek wystarczający zbieżności). Jeżeli ciąg jest monotoniczny i ograniczony to jest zbieżny.
(o trzech ciągach). Jeżeli: an≤bn≤cn dla prawie wszystkich n∈N,
Jeżeli ciągi (an) i (bn) są zbieżne oraz an≤bn dla prawie wszystkich n∈N, to:
Jeżeli lim an=a i lim bn=b, to:
Twierdzenie Stolza:
Jeżeli (nk) jest rosnącym ciągiem liczb naturalnych to ciąg (ank) nazywamy podciągiem ciągu (an).
Podciągi ciągu zbieżnego są zbieżne do granicy ciągu. Jeżeli ciąg (an) ma dwa podciągi zbieżne do różnych granic to nie jest zbieżny.
Twierdzenie Bolzano-Weierstrassa.
Granicę podciągu nazywamy punktem skupienia ciągu.
Granice ekstremalne
Ciąg jest zbieżny ⇔ granice ekstremalne istnieją i są równe.
Parę ((an),(Sn)), gdzie (an) jest ciągiem liczbowym i Sn=a1+a2+...+an nazywamy szeregiem liczbowym o wyrazie ogólnym an. Ciąg (Sn) nazywamy ciągiem sum częściowych szeregu.
Szereg Σan nazywamy zbieżnym jeżeli ciąg sum częściowych jest zbieżny.
Kryteria zbieżności szeregów:
(warunek konieczny). Jeżeli szereg Σan jest zbieżny to lim an=0.
(o zagęszczaniu Cauchy'ego). Jeżeli (an) jest malejącym do zera ciągiem liczb rzeczywistych, to szereg Σan jest zbieżny ⇔ szereg Σ2na2n jest zbieżny. Z twierdzenia tego wynika:
(kryterium porównawcze). Jeżeli 0≤an≤bn dla prawie wszystkich n∈N, to:
(kryterium Cauchy'ego)Jeżeli an≥0 dla n∈N
(kryterium d'Alemberta)
Szereg Σan nazywamy zbieżnym bezwzględnie, jeżeli szereg Σ|an| jest zbieżny. Jeżeli szereg Σan jest zbieżny i nie jest zbieżny bezwzględnie, to nazywamy go szeregiem zbieżnym względnym. Każdy szereg liczbowy bezwzględnie jest zbieżny.
Jeżeli (an) jest malejącym do zera ciągiem liczb rzeczywistych to Σ (-1)n-1⋅an nazywamy szeregiem naprzemiennym.
Kryterium Leibniza - każdy szereg naprzemienny jest zbieżny.
Iloczyn Cauchy'ego
Twierdzenie Cauchy'ego
Parę (X,d), gdzie X jest niepustym zbiorem, d jest funkcją przekształcającą XxX w zbiór liczb rzeczywistych spełniającą warunki:
∀x∈X (d(x,y)=0 ⇔ x=y)
∀x,y∈X (d(x,y)=d(y,x))
∀x,y,z∈X (d(x,y)+d(y,z) ≥ d(x,z)) nazywamy przestrzenią metryczną.
Kula otwarta o środku xo i promieniu r>0 w przestrzeni nazywamy zbiór: K(xo,r)={x∈X; d(xo,x)<r}.
Zbiór A⊂X nazywamy zbiorem otwartym w (X,d), jeżeli:
Zbiór A⊂X nazywamy zbiorem domkniętym w (X,d) jeżeli jego dopełnienie
Zbiór A⊂X nazywamy ograniczonym w (X,d), jeżeli zawiera się w pewnej kuli.
Punkt s∈X nazywamy punktem skupienia zbioru A⊂X, jeżeli w każdej kuli o środku w punkcie s znajdują się elementy zbioru A różne od siebie.
Punkt xo∈A nazywamy punktem izolowanym zbioru A, jeżeli nie jest punktem skupienia zbioru A.
Ciągiem w przestrzeni metrycznej (X,d) nazywamy każdą funkcję f:N→X.
Definicja granicy ciągu w przestrzeni metrycznej.
Ciąg (xn) nazywamy ciągiem Cauchy'ego jeżeli:
Ciąg liczb rzeczywistych spełnia warunek Cauchy'ego witw, gdy jest zbieżny.
Przestrzeń metryczną, której każdy ciąg Cauchy'ego jest zbieżny do elementu tej przestrzeni nazywamy przestrzenią zupełną.
Przestrzeń metryczną nazywamy zwartą jeżeli z każdego ciągu elementów tej przestrzeni można wybrać podciąg zbieżny do elementu tej przestrzeni.
Jeżeli X⊂R, to (X,d) jest przestrzenią zwartą witw, gdy X jest domknięty i ograniczony w E1.
Definicja granicy w sensie Cauchy'ego:
Definicja granicy w sensie Heinego:
Jeżeli f jest określona w pewnym sąsiedztwie punktu xo, to granica funkcji f w punkcie xo istnieje i równa się g witw, gdy granice jednostronne istnieją i są równe.
Jeżeli lim f(x)=g1 i lim g(x)=g2, to:
(o trzech funkcjach) Jeżeli funkcje f, g i h spełniają w pewnym sąsiedztwie punktu xo nierówność f(x)≤g(x)≤h(x) oraz lim f(x) = lim h(x)=g, to lim g(x)=g.
(Twierdzenie Bolzano-Cauchy'ego)
Odwzorowaniem T:A⊂X→Y nazywamy ciągłym w xo∈A, w sensie Cauchy`ego, jeżeli:
Odwzorowaniem T:A⊂X→Y nazywamy ciągłym w xo∈A, w sensie Heinego, jeżeli:
Jeżeli xo jest punktem skupienia zbioru A to odwzorowanie T:A⊂X→Y jest ciągłe w xo∈A witw, gdy lim T(x)=T(xo).
Własności funkcji ciągłych:
Superpozycja funkcji ciągłych jest funkcją ciągłą,
Suma, różnica, iloczyn i iloraz (tam gdzie jest określony) funkcji ciągłych jest funkcją ciągłą,
Jeżeli funkcja f jest określona w przedziale otwartym (a,b) ciągła w punkcie xo∈(a,b) i f(xo)>0 (f(xo)<0), to istnieje otoczenie punktu xo zawarte w (a,b), w którym f(x)>0 (f(x)<0),
Każda funkcja ciągła w przedziale domkniętym <a,b> jest ograniczona i osiąga kresy,
Każda funkcja ciągła w przedziale domkniętym <a,b> przyjmuje wszystkie wartości pośrednie pomiędzy kresami,
Własność Darboux, Zasada Banacha... .
Twierdzenie Weierstrassa - obraz ciągu zbioru zwartego w przestrzeni metrycznej jest zbiorem zwartym.
Odwzorowanie T: X→Y nazywamy ciągłym jednostajnie w zbiorze A⊂X, jeżeli:
(Twierdzenie Cantora) Każda funkcja ciągła w <a,b> jest ciągła jednostajnie w <a,b>.
Pochodną funkcji f w punkcie xo∈U nazywamy granicę:
Funkcję f:U⊂R→R nazywamy różniczkowalną w punkcie xo∈U jeżeli istnieją liczba rzeczywista L i funkcja r(xo,h) takie, że f(xo+h)=f(xo)+Lh+r(xo,h) i
Różniczką funkcji f w punkcie xo nazywamy f'(xo)⋅h. df(xo,h)=f'(xo)⋅h - różniczka pierwszego rzędu.
Własności pochodnej:
Jeżeli funkcje są różniczkowalne to... (wzory na suma, iloczyn i iloraz),
Jeżeli f jest bijekcją różniczkowalną w xo i f'(xo)≠0, to funkcja odwrotna f -1 jest różniczkowalna w punkcie yo=f(xo) i (f -1)'(yo)=1/f'(xo),
Jeżeli f jest funkcją różniczkowalną w xo i g jest funkcją różniczkowalną w punkcie yo=f(xo) to superpozycja gof jest funkcją różniczkowalną w punkcie xo to: (gof)'(xo)=g'(f(xo))f'(xo).
Jeżeli funkcja f jest różniczkowalna w otoczeniu U punktu xo i jej pochodna f':U→R ma w xo pochodną to nazywamy ją pochodną drugiego rzędu (druga pochodna) funkcji f w punkcie xo.
Jeżeli f jest (n-1)-krotnie różniczkowalna w otoczeniu U punktu xo i f(n-1):U→R ma w xo pochodną to nazywamy ją n-tą pochodną funkcji f w punkcie xo.
Jeżeli funkcja f jest n-krotnie różniczkowalna w punkcie xo to f(n)(xo)⋅hn nazywamy n-tą różniczką funkcji f w punkcie xo.
Funkcją f nazywamy funkcją klasy Cn w zbiorze otwartym U⊂R, jeżeli ma n-tą pochodną ciągłą w zbiorze U. Jeżeli f ma pochodną dowolnego rzędu w U to nazywamy funkcją klasy C∞.
Wzór Leibniza
Twierdzenie Rolle'a
Twierdzenie Langrange'a (tw. o wartości średniej)
Zastosowanie twierdzenia Langrage'a
Twierdzenie Cauchy'ego
Twierdzenie i wzór Taylora
Funkcję f nazywamy wypukłą w przedziale A, jeśli:
Jeżeli f jest różniczkowalna w (a,b) to jest wypukła (wklęsła) w tym przedziale witw, gdy:
Funkcja różniczkowalna w (a,b) jest wypukła (wklęsła) w tym przedziale witw, gdy pochodna f' jest funkcją niemalejącą (nierosnącą).
Funkcja dwukrotnie różniczkowalna w (a,b) jest wypukła (wklęsła) witw, gdy f''(x)≥0 (f''(x)≤0) dla każdego x∈(a,b).
Punkt xo nazywamy punktem przegięcia funkcji f określonej w pewnym otoczeniu punktu xo jeżeli dla x<xo f jest wypukła (wklęsła) i dla x>xo f jest wklęsła (wypukła).
Jeżeli xo jest punktem przegięcia funkcji dwukrotnie różniczkowalnej to f''(xo)=0.
Jeżeli funkcja f jest dwukrotnie różniczkowalna w pewnym otoczeniu punktu xo i f''≤0 (≥0) dla x<xo oraz f''≥0 (≤0) dla x>xo, to xo jest punktem przegięcia funkcji f.
Jeżeli funkcja f jest określona w przedziale (a,xo) i lim f(x)=±∞, to prostą o równaniu x=xo nazywamy asymptotą pionową lewostronną. Jeżeli lim f(x)= ±∞ to prostą o równaniu x=xo nazywamy asymptotą pionową prawostronną. Prostą x=xo nazywamy asymptotą obustronną jeżeli jest asymptotą lewo- i prawostronną.
Jeżeli funkcja f jest określona w przedziale (a,+ ∞) to prostą y=ax+b nazywamy asymptotą ukośną w ±∞ funkcji f, jeżeli lim[f(x)-ax-b]=0.
Funkcją F nazywamy funkcję pierwotną funkcji f w przedziale (a,b), jeżeli F'(x)=f(x) dla każdego x należącego do (a,b).
Całką nieoznaczoną funkcji f w (a,b) nazywamy klasę (rodzinę) wszystkich funkcji pierwotnych danej funkcji. ∫f(x)dx=F(x)+C
Twierdzenie o całkowaniu przez części
Twierdzenie o całkowaniu przez podstawienie
Przyporządkowanie każdej liczbie naturalnej pewnego podziału przedziału domkniętego <a,b> nazywamy ciągiem podziałów przedziału <a,b>.
Jeżeli istnieje granica ciągu (σn) dla każdego normalnego ciągu podziałów przedziału <a,b> i nie zależy od wyboru punktów ti to nazywamy całką oznaczoną funkcji f w przedziale <a,b>.
Własności:
Jeżeli funkcje f i g są całkowalne w <a,b>, to:
Jeżeli funkcja f jest całkowalna w <a,b> i a<c<b, to:
Jeżeli funkcja f jest całkowalna i nieujemna (niedodatnia) w <a,b>, to:
Jeżeli f i g są całkowalne w <a,b> i f(x)≤g(x) dla każdego x∈<a,b>, to:
Jeżeli funkcja f jest całkowalna, to |f| też jest całkowalna i zachodzi wzór:
Jeżeli f jest ciągła w <a,b>, to funkcja F jest różniczkowalna w <a,b> i zachodzi wzór: F'(x)=f(x).
Twierdzenie (zasadnicze twierdzenie rachunku całkowego)
Twierdzenie o całkowaniu przez podstawienie
Twierdzenie o całkowaniu przez części
Pierwsze twierdzenie o wartości średniej
Drugie twierdzenie o wartości średniej
Jeżeli istnieje granica:
Jeżeli istnieje granica:
Kryterium całkowe zbieżności szeregu liczbowego - Cauchy'ego
Przyporządkowanie każdej liczbie naturalnej pewnej funkcji f:X⊂R→R nazywamy ciągiem funkcyjnym określonym w zbiorze X.
Parę (fn(x),Sn(x)) gdzie fn(x) jest ciągiem funkcyjnym określonym w zbiorze X, Sn(x)=f1(x)+...+fn(x) nazywamy szeregiem funkcyjnym o wyrazie ogólnym fn(x).
Definicja zbieżności punktowej ciągu funkcyjnego.
Szereg Σfn(x) nazywamy zbieżnym punktowo w zbiorze X, jeżeli ciąg sum częściowych (Sn(x)) jest zbieżny punktowo w X.
Warunek konieczny zbieżności punktowej szeregu.
Szereg funkcyjny postaci Σan(x-xo)n gdzie an jest ciągiem liczbowym, nazywamy szeregiem potęgowym o środku xo.
Kres górny przedziału zbieżności szeregu Σ nazywamy promieniem zbieżności szeregu Σ anxn.
Twierdzenie Cauchy-Hadamarda.
Szereg potęgowy postaci:
Szereg funkcyjny postaci:
Jeżeli szereg trygonometryczny jest jednostajnie zbieżny w przedziale <-π,π>, to współczynniki an i bn tego szeregu wyrażają się wzorami:
Szereg trygonometryczny, którego współczynniki an i bn wyrażają się wzorami Eulera-Fouriera nazywamy szeregiem Fouriera funkcji f.
Pochodną cząstkową funkcji f w punkcie po względem zmiennej xi nazywamy granicę:
Funkcję f nazywamy funkcją klasy C1 w zbiorze otwartym U jeżeli pochodne cząstkowe I rzędu istnieją i są ciągłe w U.
Jeżeli f:U⊂Rn→R jest klasy C1 w U, to wektor:
Pochodną cząstkową n-tego rzędu nazywamy pochodną cząstkową pochodnej cząstkowej (n-1) rzędu.
Tw. Schwartza Jeżeli pochodne mieszane są ciągłe to są równe.
Funkcję f nazywamy funkcją klasy Cn w zbiorze otwartym U⊂Rn, jeżeli wszystkie pochodne n-tego rzędu funkcji są ciągłe w U.
Jeżeli funkcja f jest klasy Cn w zbiorze U, to różniczką n-tego rzędu funkcji f w punkcie po∈U nazywamy różniczkę różniczki (n-1) rzędu.
Funkcja f ma w punkcie po∈U maksimum (minimum) lokalne, jeżeli istnieje otoczenie V punktu po takie, że f(po)≥f(p) (f(po)≤f(p)) dla każdego p∈V.
Warunek konieczny istnienia ekstremum
Warunek dostateczny istnienia ekstremum
jeżeli d2f(po,dx)>0 (<0) ∀dx≠0, to f ma w po minimum (maksimum) lokalne,
jeżeli istnieją dx i dx' takie, że d2f(po,dx)<0 i d2f(po,dx')>0, to w po f nie ma ekstremum.
Drugi warunek dostateczny istnienia ekstremum
jeżeli Mi>0 dla każdego i=1...n to funkcja f ma w punkcie po minimum lokalne,
jeżeli (-1)iMi>0 dla każdego i=1...n to funkcja f ma w punkcie po maksimum lokalne.
Funkcja f ma w punkcie po maksimum (minimum) przy warunku g(x1...xn), jeżeli istnieje otoczenie V punktu po takie, że f(po)≥f(p) (f(po)≤f(p)) dla każdego p∈V∩M.
Warunek konieczny istnienia ekstremum warunkowego
Warunek wystarczający istnienia ekstremum warunkowego
Jeżeli istnieją granica ciągu (σn) i nie zależy od wyboru normalnego ciągu podziałów prostokąta P oraz od wyboru punktów (xi,yin ) to granicę tę nazywamy całką podwójną funkcji f w P.
Jeżeli funkcje Φ i Ψ są ciągłe w przedziale <a,b>, to zbiór D={(x,y): a≤x≤b, Φ(x)≤y≤Ψ(x)} nazywamy obszarem normalnym względem osi OX.
Jeżeli funkcje g i h są ciągłe w przedziale <c,d>, to zbiór D={(x,y): c≤y≤d, g(y)≤x≤h(y)} nazywamy obszarem normalnym względem osi OY.
Równanie x'=f(x,t), gdzie f jest funkcją f:Ux<a,b>→R nazywamy równaniem różniczkowym zwyczajnym pierwszego rzędu. Rozwiązaniem równania x'=f(x,t) nazywamy funkcję x:<a,b>→U taką, że x'(t)=f(x(t),t).
Pole obszaru płaskiego
obszar ograniczony funkcją i osią x
obszar ograniczony dwoma funkcjami
obszar ograniczony równaniami parametrycznymi
obszar ograniczony krzywą określoną równaniem biegunowym
Długość łuku krzywej
Objętość bryły obrotowej
Pole powierzchni bocznej bryły obrotowej
![]()
![]()
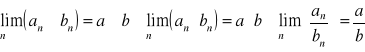
jeżeli:
- bn→+∞,
- an≥bn dla prawie wszystkich n∈N
- ![]()
PODCIĄGI
Każdy ograniczony ciąg liczb rzeczywistych zawiera podciąg zbieżny.
lim sup an = sup S (sup - superium)
lim inf an = inf S (inf - inferior)
SZEREGI LICZBOWE
- szereg harmoniczny dla α>1 jest zbieżny,
- szereg harmoniczny dla α≤1 jest rozbieżny.
- jeżeli Σbn jest zbieżny, to Σan jest zbieżny,
- jeżeli Σbn jest rozbieżny, to Σan jest rozbieżny.
![]()
- jeżeli g<1 to Σan jest zbieżny,
- jeżeli g>1 to Σan jest rozbieżny,
- jeżeli g=1 to ???
Jeżeli an≥0 dla n∈N
![]()
- jeżeli g<1 to Σan jest zbieżny,
- jeżeli g>1 to Σan jest rozbieżny,
- jeżeli g=1 to ???
Iloczynem Cauchy'ego szeregów Σan i Σbn nazywamy szereg ΣCn taki, że Cn=Σakbn-k
Jeżeli szeregi Σan i Σbn są zbieżne odpowiednio do S1 i S2 i przynajmniej jeden z nich jest zbieżny bezwzględnie to iloczyn Cauchy'ego tych jest zbieżny i jego suma równa się S1⋅S2.
PRZESTRZEŃ METRYCZNA
Funkcję d nazywamy metryką lub odległością.
∀x∈A ∃r>0(K(x,r)⊂A).
X-A jest zbiorem otwartym w (X,d).
![]()
![]()
GRANICE
![]()
![]()
- lim [f(x)±g(x)]=g1±g2
- lim [f(x)⋅g(x)]=g1⋅g2
- lim [f(x)/g(x)]=g1/g2
Jeżeli funkcja f jest określona w pewnym sąsiedztwie punktu xo, to ma granicę w xo witw, gdy:
![]()
ODWZOROWANIA CIĄGŁE
![]()
![]()
![]()
POCHODNE
![]()
![]()
POCHODNE WYŻSZYCH RZĘDÓW
Jeżeli funkcje U i V są n-krotnie różniczkowalne w xo, to:
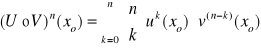
Jeżeli funkcja f jest ciągła w <a,b> i różniczkowalna w (a,b) oraz f(a)=f(b) to istnieje punkt c∈(a,b) taki, że f'(c)=0.
Jeżeli funkcja f jest ciągła w <a,b> i różniczkowalna w (a,b) to istnieje punkt c∈(a,b) taki, że:
![]()
Tw1. Jeżeli f jest różniczkowalna w (a,b) i f'(x)=0, to f jest stała.
Tw2. Jeżeli f jest różniczkowalna w (a,b) i f'(x)>0 (f'(x)<0), dla x∈(a,b), to f jest rosnąca (malejąca) w (a,b)
Jeżeli funkcje U i V są ciągłe w (a,b) i różniczkowalne w (a,b) oraz V'(x)≠0 dla x∈(a,b) to istnieje punkt c∈(a,b) taki, że:
![]()
Jeżeli funkcja f:U⊂R→R jest różniczkowalna (n+1)-krotnie w zbiorze otwartym U oraz <xo,x>⊂U, to istnieje punkt c∈(xo,x) taki, że:
![]()
Jeżeli xo=0 to wzór Taylora nazywamy wzorem Maclaurina.
FUNKCJE WYPUKŁE I WKLĘSŁE
∀x1,x2∈A ∀λ∈<0,1> [f(λx1+(1-λ)x2)≤ λf(x1)+(1-λ)f(x2)]
Jeżeli zachodzi nierówność odwrotna to funkcję nazywamy wklęsłą w przedziale A.
F(x)≥f(xo)+f'(xo)(x-xo) dla x,xo∈(a,b)
F(x)≤f(xo)+f'(xo)(x-xo) dla x,xo∈(a,b)
PUNKTY PRZEGIĘCIA
ASYMPTOTY
CAŁKA NIEOZNACZONA
Jeżeli funkcje u i v są klasy C1, to prawdziwy jest wzór:
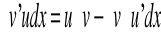
Jeżeli funkcja g:(a,b)→ (α,β) jest klasy C1, funkcja f:(α,β)→R jest ciągła, to:
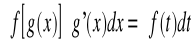
CAŁKA OZNACZONA (RIEMANA)
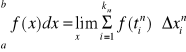
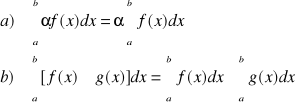
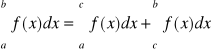
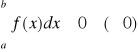
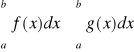
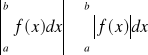
Jeżeli f jest ciągła w <a,b> i G jest funkcją pierwotną funkcji f, to:
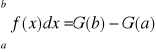
- wzór Newtona-Leibniza
Jeżeli f:<a,b>→R jest ciągła, funkcja g:<α,β>→<a,b> jest klasy C1 oraz g'(t)≠0 i g(α)=a i g(β)=b, to:
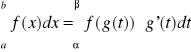
Jeżeli funkcje u i v są klasy C1, to:
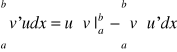
Jeżeli funkcja f jest ciągła w <a,b>, funkcja g jest całkowalna i ma stały znak w <a,b>, to:
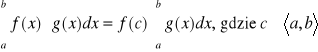
Jeżeli funkcja f jest ciągła w <a,b>, funkcja g jest klasy C1 i monotoniczna w <a,b>, to istnieje c∈<a,b> takie, że:
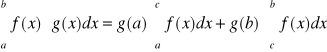
CAŁKI NIEWŁAŚCIWE
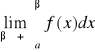
to granicę tę nazywamy całką niewłaściwą I rodzaju. Jeżeli nie istnieje granica, to całkę nazywamy rozbieżną. Analogicznie definiujemy:
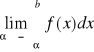
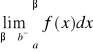
to granicę tę nazywamy całką niewłaściwą II rodzaju. Jeżeli nie istnieje granica, to całkę nazywamy rozbieżną. Analogicznie definiujemy:
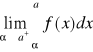
Jeżeli funkcja f jest ciągła w <1,+∞) oraz nieujemna i malejąca do 0 w tym przedziale, to szereg Σf(n) jest zbieżny ⇔ ∫ f(x)dx jest zbieżna.
CIĄGI I SZEREGI FUNKCYJNE
Ciąg (fn(x)) nazywamy zbieżnym punktowo w zbiorze X do funkcji f(x), jeżeli:
![]()
Jeżeli Σfn(x) jest zbieżny punktowo w zbiorze X, to ciąg (fn(x)) jest zbieżny punktowo do funkcji f(x)=0 dla x∈X.
SZEREGI POTĘGOWE
Jeżeli:
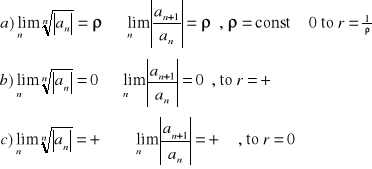
![]()
nazywamy szeregiem Taylora o środku w punkcie xo funkcji f.
Jeżeli xo=0 to szereg nazywamy szeregiem Maclaurina.
SZEREG FOURIERA
![]()
nazywamy szeregiem trygonometrycznym.
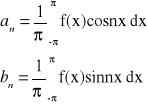
Wzory powyższe nazywają się wzorami Eulera-Fouriera.
FUNKCJE WIELU ZMIENNYCH
![]()
![]()
nazywamy gradientem funkcji f w zbiorze U.
EKSTREMA LOKALNE FUNKCJI WIELU ZMIENNYCH
Jeżeli funkcja f ma w punkcie po ekstremum to grad f(po)=0.
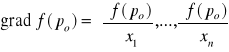
Jeżeli f jest klasy C2 w otoczeniu punktu po i grad f(po)=0, to:
EKSTREMA WARUNKOWE
F(x1,...,xn;λ)=f(x1,…,xn)+λg(x1,…,xn). Jeżeli f ma w punkcie po ekstremum warunkowe to istnieje liczba rzeczywista taka, że:
![]()
Jeżeli:
![]()
to: jeżeli d2F(po,λo,dx)>0 (<0) przy warunku dg(po,dx)=0 dla każdego dx≠0, to funkcja f ma w punkcie po minimum warunkowe (maksimum warunkowe).
CAŁKA PODWÓJNA
RÓWNANIA RÓŻNICZKOWE
ZASTOSOWANIE CAŁKI PODWÓJNEJ
1. Pole obszaru płaskiego
![]()
2.Objętość bryły
![]()
3. Pole powierzchni
![]()
ZASTOSOWANIE GEOMETRYCZNE CAŁKI OZNACZONEJ
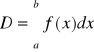
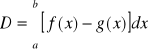
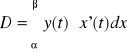
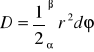
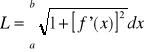
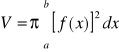
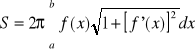
Pusta
Wyszukiwarka
Podobne podstrony:
Analiza matematyczna Wykłady, GRANICE FUNKCJI
Analiza matematyczna Wykłady, CIAGI LICZBOWE
Analiza matematyczna wykład(1)(1)
Analiza matematyczna. Wykłady CAŁKI NIEOZNACZONE
Analiza matematyczna. Wykłady GRANICE FUNKCJI
Analiza matematyczna Wykłady, CAŁKI NIEOZNACZONE
Analiza matematyczna Wykłady, POCHODNE FUNKCJI
Wyklad-02-AM1, Analiza matematyczna, Analiza matematyczna, Wykłady
Wyklad-07-08-AM1, Analiza matematyczna, Analiza matematyczna, Wykłady
Analiza matematyczna. Wykłady TWIERDZENIA RACHUNKU RÓŻNICZKOWEGO
Analiza matematyczna. Wykłady CIAGLOSC FUNKCJI
Wyklad-04-AM1, Analiza matematyczna, Analiza matematyczna, Wykłady
Wyklad-10-AM1, Analiza matematyczna, Analiza matematyczna, Wykłady
Algebra i Analiza Matematyczna, wykład 1, 06 10 2001-10-09
Wyklad-09-AM1, Analiza matematyczna, Analiza matematyczna, Wykłady
Analiza matematyczna wykład(1)
więcej podobnych podstron