Metoda najmniejszych kwadratów

W praktyce laboratoryjnej często spotykanym problemem jest sprawdzenie przewidywanej teoretycznie zależności funkcyjnej zachodzącej pomiędzy dwiema wielkościami fizycznymi, a także wyznaczenie parametrów określających tę funkcję.

Wykonując n-krotny pomiar wielkości fizycznych Y=f(X) dostajemy zbiór n par (
) gdzie ( i=1,2, ... ,n ).

Zbiór otrzymanych punktów możemy powiązać relacją liniową postaci:

y= A + Bx

Gdzie:

A=
B=

O tej prostej mówi się, że jest dopasowana metodą najmniejszych kwadratów lub że jest prosta regresji zmiennych x i y.

Przykład:

W wyniku pomiarów wartości x i y uzyskano następujące wyniki
za pomocą metody najmniejszych kwadratów wyznaczyć równanie y=A+Bx wiążące te dwie zmienne.

= 5(1+4+9+16+25) - 225= 50

A=
=
= 2,7

B=
=
= 0,5

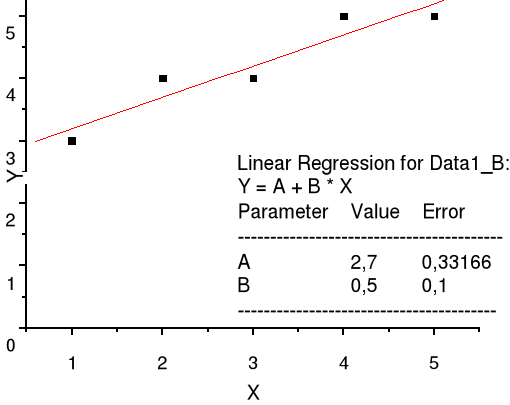
y=0,5x + 2,7

Wykres prostej regresji zmiennych x i y.

---