Rynek kapitałowy - część druga
1. Stopy zwrotu jako zmienne losowe
Kluczowymi pojęciami używanymi w trakcie wykładów dotyczących podejmowania decyzji na rynkach finansowych są niepewność i ryzyko. Unikając szerokich rozważań, niepewność odnosić będziemy do przyszłego wyniku decyzji inwestycyjnych. Inwestor podejmując w chwili obecnej decyzję inwestycyjną oczekuje założonego przez siebie wyniku decyzji. Jednakże nie ma on ani pełnej wiedzy, by przewidzieć wszystkie czynniki mogące w istotny sposób wpłynąć na zrealizowany wynik inwestycji, ani też pełnej władzy, by wpływać na te czynniki w kierunku dla niego pożądanym. Zwykle zatem okazuje się, że zrealizowany wynik inwestycji jest inny niż oczekiwany. Niepewność w czystej postaci oznacza sytuację, w której inwestor nie jest w stanie określić rozkładu możliwych wyników swojej decyzji w przyszłości. Jeśli natomiast inwestor posiada wiedzę pozwalającą na określenie rozkładu możliwych wyników swojej decyzji, mówimy o ryzyku. Wynika z tego, że wynik inwestycji (stopa zwrotu z inwestycji) w warunkach ryzyka umożliwia jego traktowanie jako zmienną losową. Ryzyko jest zatem ,,niepewnością mierzalną''. Na przykład, chociaż nie możemy być pewni jakiegokolwiek ustalonego zysku z naszej inwestycji w danym roku, to możemy wiedzieć, że możliwe zyski z tej inwestycji mają rozkład normalny o danym oczekiwanym zysku i określonej wariancji. Niepewność jest definiowana natomiast jako sytuacja, w której możliwe są różne wyniki naszej inwestycji, ale informacje o rozkładzie prawdopodobieństwa tych wyników są albo nieznane albo niekompletne. Nie popełnimy jednak dużego błędu, gdy w języku potocznym pojęcia ryzyko i niepewność będą używane zamiennie.
Zmienna losowa to taka zmienna, która przybiera określone wartości (zmienna skokowa) lub wartości z określonych przedziałów (zmienna ciągła) z określonymi prawdopodobieństwami. Prawdopodobieństwa te określają częstość wystąpienia danej wartości. Przyporządkowujemy je zdarzeniom polegającym na tym, że zmienna losowa przybierze określoną wartość ze zbioru wartości, które przybierać może. Określając prawdopodobieństwo zdarzenia oceniamy ,,szansę'' jego zajścia w rzeczywistości. Prawdopodobieństwo jest zatem miarą wiarygodności, którą przypisujemy danemu zdarzeniu. Prawdopodobieństwo jest liczbą z przedziału ![]()
, przy czym zdarzeniu pewnemu odpowiada prawdopodobieństwo równe jeden.
Jeśli możliwe jest wielokrotne powtarzanie doświadczenia, to prawdopodobieństwo zdarzenia określamy jako częstość jego zajścia w długiej serii doświadczeń. Np. rzucając dostatecznie dużo razy kostką do gry, zauważymy, że częstość wystąpienia jedynki (i każdej z pozostałych liczb) zbliża się do ![]()
. Częstość ta jest prawdopodobieństwem wyrzucenia jedynki. Rzucając dostatecznie dużo razy monetą zauważymy, że częstość wystąpienia orła zbliża się do ![]()
. Liczbę tą nazywamy prawdopodobieństwem wyrzucenia orła. Częstościowa interpretacja prawdopodobieństwa dotyczy więc zdarzeń powtarzalnych.
W przypadku zdarzeń niepowtarzalnych określenie ich prawdopodobieństwa polega na zbadaniu zbiorowości zdarzeń podobnych. Np. chcąc ustalić prawdopodobieństwo zdania egzaminu z pewnego przedmiotu przez osobę X, możemy przeanalizować sposób przeprowadzania egzaminu, przebieg sesji egzaminacyjnych z tego przedmiotu w przeszłości oraz stopień opanowania treści, które będą przedmiotem egzaminu i na tej podstawie ocenić to prawdopodobieństwo. W przypadku zdarzeń niepowtarzalnych stosuje się też tzw. subiektywną miarę prawdopodobieństwa. Prawdopodobieństwo subiektywne jest miarą przekonań osobistych odnośnie do szansy zajścia zdarzenia. W szczególności prawdopodobieństwo subiektywne ustalane jest przez eksperta (lub grupę ekspertów) wykorzystującego swoją wiedzę i doświadczenie. W analizie projektów inwestycyjnych taki sposób określania prawdopodobieństwa może mieć uzasadnienie.
Prawdopodobieństwo zajścia zdarzenia j-tego oznaczać będziemy przez ![]()
.
1.1. Rozkład prawdopodobieństwa stopy zwrotu
Wprowadźmy następującą definicję stopy zwrotu z inwestycji (R):
![]()
gdzie: ![]()
- wartość inwestycji w okresie początkowym, ![]()
- wartość inwestycji w okresie następnym, ![]()
- dodatkowe dochody z inwestycji wypłacone w okresie, za który obliczana jest stopa zwrotu (np. z tytułu dywidend). Przy takich oznaczeniach różnica ![]()
oznacza zysk kapitałowy, iloraz ![]()
oznacza stopę zysku kapitałowego, natomiast ![]()
- stopę dywidendy.
Upraszczając zagadnienie założymy, że stopa zwrotu w badanym okresie przyjmować może skończoną liczbę wartości ze znanymi prawdopodobieństwami. Zatem:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
gdzie prawdopodobieństwa ![]()
spełniają ![]()
oraz ![]()
.
Zapisane powyżej przyporządkowanie wartościom stopy zysku ![]()
prawdopodobieństw ich wystąpienia ![]()
określamy rozkładem prawdopodobieństwa. Przyporządkowanie to przedstawia szanse otrzymania różnych stóp zwrotu z inwestycji. Zwykle prawdopodobieństwa te nie są równe, zatem rozkład prawdopodobieństwa stóp zwrotu nie jest jednostajny. W rzeczywistości stopy zwrotu są ciągłe, w tym sensie, że można określić prawdopodobieństwo zdarzenia polegającego na tym, że stopa zwrotu przyjmie wartości rzeczywiste z pewnego przedziału. Rozkład prawdopodobieństwa opisuje funkcja gęstości rozkładu.
Przykład 1
Na następny miesiąc rozpatrywanych jest 5 wariantów rozwoju sytuacji na rynku: 1 - bardzo niekorzystny, 2 - gorszy niż przeciętnie, 3 - przeciętny, 4 - lepszy niż przeciętnie, 5 - wyjątkowo korzystny. Prawdopodobieństwa wystąpienia tych stanów oraz spodziewane stopy zwrotu w przypadku zrealizowania się danego stanu są następujące:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Rysunek 1 pokazuje rozkład prawdopodobieństwa stopy zwrotu.
Rysunek 1. Rozkład prawdopodobieństwa stopy zwrotu
![]()
1,0
0,8
0,6
0,4
0,2
-1,0 1,0 2,0 3,0 4,0 5,0 ![]()
Zmienna losowa jest opisywana za pomocą tzw. parametrów rozkładu. Parametry te charakteryzują zbiór obserwacji jakie przyjmuje zmienna losowa. Dzięki parametrom opisowym możemy za pomocą kilku liczb uzyskać dostatecznie duże wyobrażenie o rozkładzie tej zmiennej.
Znaczenie praktyczne w analizie stóp zwrotu mają następujące grupy parametrów:
charakteryzujące przeciętną wielkość stopy zwrotu (wartość oczekiwana, mediana, dominanta),
charakteryzujące rozproszenie wartości stopy zwrotu wokół wartości przeciętnej (wariancja, odchylenie standardowe, odchylenie przeciętne, semiwariancja, semiodchylenie standardowe); parametry te są miarami ryzyka związanego z inwestycją,
charakteryzujące skośność rozkładu stopy zwrotu (współczynnik asymetrii),
charakteryzujące spłaszczenie rozkładu (kurtoza),
charakteryzujące statystyczną zależność dwóch stóp zwrotu (kowariancja, współczynnik korelacji).
1.2. Wartość oczekiwana
Wartość oczekiwana stopy zwrotu ![]()
, charakteryzuje przeciętną wielkość stopy zwrotu. Informuje o tym, jakiej stopy zwrotu można się spodziewać w rozpatrywanym okresie czasu. Wartość oczekiwaną definiuje się jako:
![]()
tzn. jako ważoną prawdopodobieństwami sumę wszystkich możliwych realizacji stopy zwrotu.
Obliczenie oczekiwanej wartości stopy zwrotu przedstawiamy w tablicy 1.
Tablica 1. Obliczenie oczekiwanej wartości stopy zwrotu
|
|
|
-1,0 |
0,05 |
-0,05 |
0,0 |
0,10 |
0,00 |
1,0 |
0,30 |
0,30 |
2,0 |
0,30 |
0,60 |
3,0 |
0,20 |
0,60 |
4,0 |
0,05 |
0,20 |
X |
X |
1,65 |
Źródło: opracowanie własne
Oznacza to, że inwestor oczekiwać może stopy zwrotu równej ![]()
. Jednakże z natury zmiennej losowej wynika, że przybiera ona różne wartości z określonymi prawdopodobieństwami. Zatem inwestor nie może być pewny, że w rozpatrywanym miesiącu jego zysk wyniesie ![]()
. Występuje niepewność co do spodziewanego dochodu, czyli ryzyko otrzymania dochodu innego niż dochód oczekiwany. Tak zdefiniowane ryzyko mierzą parametry określające rozproszenie realizacji zmiennej losowej wokół jej wartości oczekiwanej.
1.3. Wariancja i odchylenie standardowe stopy zwrotu
Wariancja ![]()
jest to średnie kwadratowe odchylenie stopy zwrotu od jej wartości oczekiwanej. Wzór na wariancję jest następujący:
![]()
.
Wariancja jest wyrażona w ![]()
, jeśli stopa zwrotu jest wyrażona w ![]()
. Im większe rozproszenie stopy zwrotu wokół średniej, tym większa wariancja, tym większe ryzyko, że zrealizowany zysk będzie różny od zysku oczekiwanego.
Odchylenie standardowe ![]()
, definiowane jako:
![]()
jest miarą rozproszenia wyrażoną w ![]()
, tak jak stopa zwrotu. Oznacza ono o ile przeciętnie rzecz biorąc (in plus, in minus) stopa zwrotu może odchylać się od oczekiwanej stopy zwrotu. Jest to zatem także miara ryzyka związanego z daną inwestycją.
Obliczenie wariancji stopy zwrotu zamieszczamy w tablicy 2.
Tablica 2. Obliczenie wariancji stopy zwrotu
|
|
|
|
|
-1,0 |
0,05 |
-2,650 |
7,023 |
0,351 |
0,0 |
0,10 |
-1,650 |
2,723 |
0,272 |
1,0 |
0,30 |
-0,650 |
0,423 |
0,127 |
2,0 |
0,30 |
0,350 |
0,123 |
0,037 |
3,0 |
0,20 |
1,350 |
1,823 |
0,365 |
4,0 |
0,05 |
2,350 |
5,523 |
0,276 |
X |
X |
X |
X |
1,428 |
Źródło: opracowanie własne
Wariancja stopy zwrotu równa ![]()
określa średnie kwadratowe odchylenie realizacji stopy zwrotu od oczekiwanej stopy zwrotu równej ![]()
. Odchylenie standardowe stopy zwrotu wynosi zatem:
![]()
i oznacza w naszym przypadku, że średnio rzecz biorąc realizacje stopy zwrotu odchylać się mogą od oczekiwanej wartości stopy zwrotu równej ![]()
o ![]()
. Czy obliczone wyżej ryzyko jest wysokie w stosunku do oczekiwanej stopy zwrotu? Aby odpowiedzieć na to pytanie rozważmy przykład drugi. W tablicy 3 podano drugi przykładowy rozkład stopy zwrotu.
Tablica 3. Obliczenie parametrów rozkładu stopy zwrotu
|
|
|
|
|
|
-1 |
0,2 |
-0,2 |
-1,4 |
1,96 |
0,392 |
0 |
0,3 |
0 |
-0,4 |
0,16 |
0,048 |
1 |
0,4 |
0,4 |
0,6 |
0,36 |
0,144 |
2 |
0,1 |
0,2 |
1,6 |
2,56 |
0,256 |
X |
X |
0,4 |
X |
X |
0,84 |
Źródło: opracowanie własne
Oznacza to, że inwestor oczekiwać może w tym przypadku stopy zwrotu równej ![]()
, natomiast odchylenie standardowe stopy zwrotu wynosi:
![]()
i oznacza, że średnio rzecz biorąc realizacje stopy zwrotu odchylać się mogą od oczekiwanej wartości stopy zwrotu równej ![]()
o ![]()
.
Zatem w drugim przypadku odchylenie standardowe jest mniejsze niż w przypadku inwestycji pierwszej. Czy jednak w relacji do oczekiwanej stopy zwrotu obecnie ryzyko inwestycji drugiej jest również mniejsze?.
1.4. Współczynnik zmienności - ryzyko relatywne
Wprowadźmy relatywną miarę ryzyka zwaną współczynnikiem zmienności stopy zwrotu i definiowaną jako:
![]()
.
Współczynnik ten określa, jaką część oczekiwanego poziomu stopy zwrotu stanowi jego odchylenie standardowe. Inaczej mówiąc, określa on ile jednostek ryzyka przypada na jednostkę wartości oczekiwanej. Jest zrozumiałe, że walor jest tym bezpieczniejszy im ![]()
jest bliższe zera. Współczynnik ten umożliwia porównanie ryzyka w różnych inwestycjach (projektach). W rozpatrywanych dwóch przypadkach mamy:
Tablica 4. Ryzyko względne - porównanie inwestycji
Inwestycja I |
Inwestycja II |
||
|
|
|
|
1,65 |
1,195 |
0,40 |
0,917 |
x |
V=0,724 |
x |
V=2,293 |
Źródło: opracowanie własne
Zatem inwestycja I jest o bardziej bezpieczna niż II, mimo że ryzyko mierzone odchyleniem standardowym stopy zwrotu jest w przypadku I większe. W przypadku pierwszym na jednostkę oczekiwanego zysku przypada 0,724 jednostki ryzyka, natomiast w przypadku drugim na jednostkę oczekiwanego zysku przypada aż 2,293 jednostki ryzyka.
1.5. Semiwariancja i semiodchylenie standardowe
Inwestor niekiedy chciałby mieć wyobrażenie jakiego ryzyka może się spodziewać w sytuacji gorszej niż przeciętna. Do oceny takiego ryzyka służy semiwariancja stopy zwrotu, czyli wariancja ujemnych odchyleń od wartości oczekiwanej. Jest ona definiowana jako:
![]()
gdzie:
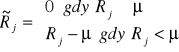
.
Zatem wariancja ujemnych odchyleń pokazuje średnie kwadratowe odchylenie stopy zwrotu od wartości oczekiwanej w sytuacji niepomyślnej (gorszej niż przeciętna). Semiodchylenie standardowe jest definiowane jako:
![]()
i oznacza przeciętne odchylenie realizacji stopy zwrotu mniejszych od oczekiwanej stopy zysku od tej wartości.
Obliczenia semiwariancji stopy zwrotu przedstawiamy w tablicy 5.
Tablica 5. Obliczenie semiwariancji stopy zwrotu
|
|
|
|
|
|
-1,0 |
0,05 |
-2,65 |
-2,65 |
7,023 |
0,351 |
0,0 |
0,10 |
-1,65 |
-1,65 |
2,723 |
0,272 |
1,0 |
0,30 |
-0,65 |
-0,65 |
0,423 |
0,127 |
2,0 |
0,30 |
0,35 |
0 |
0 |
0 |
3,0 |
0,20 |
1,35 |
0 |
0 |
0 |
4,0 |
0,05 |
2,35 |
0 |
0 |
0 |
X |
X |
X |
X |
X |
0,750 |
Źródło: opracowanie własne
Widzimy, że semiwariancja jest mniejsza od obliczonej poprzednio wariancji. Jest tak zawsze, gdyż semiwariancja obejmuje tylko odchylenia ujemne. Semiodchylenie standardowe stopy zwrotu równe:
![]()
mówi, że średnio rzecz biorąc wartości stopy zwrotu odchylają się od in minus od oczekiwanej stopy zwrotu o 0,866%.
1.6. Wartość informacyjna parametrów rozkładu. Rozkład normalny
Zastanówmy się, kiedy omówione wyżej parametry rozkładu stopy zwrotu dają poprawną i wystarczającą charakterystykę tego rozkładu. Rozpocznijmy od pokazania krzywej gęstości rozkładu normalnego. Na rysunku widzimy, że jest to rozkład symetryczny wokół średniej oraz, że średnia jest jednocześnie wartością środkową i dominującą. Zatem w takim rozkładzie wartość oczekiwana stopy zwrotu najlepiej oddaje ,,centralną tendencję'' stopy zwrotu. Podobnie miary ryzyka, które podaliśmy są wystarczającymi miarami rozproszenia wokół średniej. Zauważmy, że do przedziału ![]()
(,,trzech sigm'') trafiają prawie wszystkie realizacje stopy zwrotu pochodzące z rozkładu normalnego (dokładnie 99.7%).
Rysunek 2. Funkcja gęstości rozkładu normalnego standaryzowanego
f(z)
z
W praktyce spotykamy się z rozkładami stóp zwrotu odbiegającymi od normalnych. Są to rozkłady:
skośne prawostronnie lub lewostronnie, a więc niesymetryczne wokół wartości oczekiwanej,
z pogrubionymi lub uciętymi ogonami (symetrycznie lub niesymetrycznie).
W ramach bardzo skrótowego powtórzenia pomijamy problemy związane badaniem skośności i spłaszczenia rozkładów, odsyłając do podstawowych podręczników ze statystyki.
1.7. Miary statystycznej współzależności (skorelowania)
Na rynku kapitałowym występują różne walory, które mogą być przedmiotem zainteresowania inwestora. Mogą się one charakteryzować różną płynnością, różnym poziomem oczekiwanych zysków, różnym ryzykiem i inną zmiennością w różnych okresach czasu. Jak wiemy i jak szczegółowo opowiemy w następnych częściach zajęć, wszystko to może być wykorzystane do konstrukcji portfeli ograniczających ryzyko.
Rozważmy dwie ryzykowne inwestycje A i B mające różne rozkłady stopy zysku. Oznaczmy je przez ![]()
i ![]()
. Niech charakteryzują się one następującymi parametrami rozkładu ![]()
, ![]()
oraz ![]()
, ![]()
. Miarą statystycznej zależności między stopami zwrotu dwóch walorów jest kowariancja definiowana jako:
![]()
,
gdzie ![]()
jest prawdopodobieństwem łącznej realizacji stóp zwrotu ![]()
.
Statystyczna zależność jest dodatnia ![]()
, wtedy gdy w rozkładzie prawdopodobieństwa odchylenia od wartości oczekiwanej jednej stopy zwrotu są takich samych znaków jak odchylenia od wartości oczekiwanej drugiej stopy zwrotu. Mówimy, że obie stopy zwrotu zmieniają się w tym samym kierunku. Statystyczna zależność jest ujemna, gdy w rozkładzie prawdopodobieństwa odchylenia od wartości oczekiwanej jednej stopy zwrotu są różnych znaków niż odchylenia od wartości oczekiwanej drugiej stopy zwrotu. Mówimy, że stopy zwrotu zmieniają się w odwrotnym kierunku. Wreszcie brak statystycznej zależności ![]()
oznacza, że zmiany jednej stopy zwrotu względem zmian drugiej są czysto losowe. Zależność statystyczna może występować z różną siłą. Zatem prawidłowości zmian mogą być zakłócane losowo. Ocena siły związku statystycznego za pomocą kowariancji jest utrudniona z uwagi na nieunormowanie tego parametru (przedział zmienności zależy od jednostek w jakich wyrażone są badane zmienne). Wady tej nie ma współczynnik korelacji (liniowej) definiowany jako:
![]()
.
Współczynnik korelacji jest więc kowariancją, podzieloną przez iloczyn odchyleń standardowych stóp zwrotu. Współczynnik korelacji i kowariancja muszą mieć te same znaki. Współczynnik korelacji spełnia nierówność:
![]()
.
Zatem:
jeśli
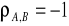
mówimy o ścisłej korelacji ujemnej, wzrostowi stopy zwrotu A odpowiada zawsze taki sam (z dokładnością do stałej) spadek stopy zwrotu B i odwrotnie,jeśli
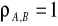
mówimy o ścisłej korelacji dodatniej, wzrostowi stopy zwrotu A odpowiada zawsze taki sam (z dokładnością do stałej) wzrost stopy zwrotu B i odwrotnie,jeśli
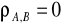
mówimy o braku skorelowania, zmiany stóp zwrotu są względem siebie czysto losowe lub jedna ze stóp zwrotu nie wykazuje zmienności.w pozostałych przypadkach tj.
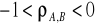
oraz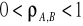
mówimy odpowiednio o korelacji ujemnej i dodatniej, przy czym dla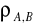
bliskiego zero o korelacji słabej, dla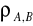
bliskiego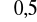
o korelacji umiarkowanej, dla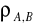
bliskiego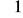
o korelacji silnej.
Rozpatrzmy dwie akcje, których łączny rozkład prawdopodobieństwa stóp zwrotu jest dany w tablicy 6.
Tablica 6. Parametry rozkładu dwóch stóp zwrotu
|
|
|
|
|
|
|
|
|
-2 |
1 |
0,05 |
-0,1 |
0,05 |
6,25 |
0,0225 |
0,3125 |
0,001125 |
-1 |
1 |
0,2 |
-0,2 |
0,2 |
2,25 |
0,0225 |
0,4500 |
0,004500 |
0 |
2 |
0,2 |
0 |
0,4 |
0,25 |
0,7225 |
0,0500 |
0,144500 |
1 |
0 |
0,35 |
0,35 |
0 |
0,25 |
1,3225 |
0,0875 |
0,462875 |
2 |
3 |
0,15 |
0,3 |
0,45 |
2,25 |
3,4225 |
0,3375 |
0,513375 |
3 |
1 |
0,05 |
0,15 |
0,05 |
6,25 |
0,0225 |
0,3125 |
0,001125 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Źródło: opracowanie własne
Tablica 7.Kowariancja pomiędzy stopami zwrotu dwóch walorów
|
|
|
|
|
|
-2 |
1 |
0,05 |
-2,5 |
-0,15 |
0,01875 |
-1 |
1 |
0,2 |
-1,5 |
-0,15 |
0,04500 |
0 |
2 |
0,2 |
-0,5 |
0,85 |
-0,08500 |
1 |
0 |
0,35 |
0,5 |
-1,15 |
-0,20125 |
2 |
3 |
0,15 |
1,5 |
1,85 |
0,41625 |
3 |
1 |
0,05 |
2,5 |
-0,15 |
-0,01875 |
|
|
|
|
|
|
Źródło: opracowanie własne
Kowariancja między stopami zwrotu akcji A i B jest dodatnia. Ażeby ocenić siłę związku statystycznego lepiej jest wykorzystać współczynnik korelacji. Na podstawie danych zawartych w tablicy możemy zapisać, że:
![]()
.
Oznacza to słabą dodatnią korelację między stopami zwrotu A i B.
Do tej pory zakładaliśmy, że stopy zwrotu w okresie przyszłym (którego dotyczą decyzje inwestora) miały znane rozkłady prawdopodobieństwa. Umożliwiało to obliczenie podstawowych parametrów rozkładu zgodnie z podanymi wyżej wzorami. Założenie to jest bardzo rygorystyczne. Nie mamy informacji a priori o rozkładach stóp zwrotu w okresach przyszłych. Powszechną praktyką jest wykorzystanie informacji o historycznych, zaobserwowanych stopach zwrotu w celu oszacowania parametrów ich rozkładu w okresach przyszłych.
1.8. Zaobserwowane stopy zwrotu
Historyczne, zaobserwowane ceny danego waloru oznaczać będziemy:
![]()
; ![]()
gdzie T oznacza liczbę okresów z przeszłości (np. sesji, tygodni, itp.), z których pochodzą obserwacje. W przypadku rozpatrywania wielu akcji ceny (i wszystkie pozostałe zmienne) oznaczone będą dodatkowym indeksem informującym o jaką akcję chodzi np. ![]()
, ![]()
. Dywidenda wypłacona w okresie przeszłym ![]()
oznaczana będzie ![]()
. Jednookresową stopę zwrotu dla danego waloru w okresie t oznaczymy
![]()
.
W tablicy 8 podajemy zaobserwowane stopy zwrotu dla kilku walorów oraz WIG-u na wybranych sesjach (w procentach).
Tabela 8. Szeregi czasowe zaobserwowanych stóp zwrotu wybranych akcji
data |
t |
ragros |
rambank |
ramica |
rampli |
rams |
ranimex |
rapator |
rapexim |
rwig |
00-10-26 |
1 |
0,00 |
0,00 |
-1,00 |
-0,71 |
-2,64 |
-2,06 |
0,00 |
0,97 |
-1,00 |
00-10-27 |
2 |
0,00 |
-0,38 |
-3,03 |
4,32 |
0,39 |
-0,90 |
0,93 |
-1,44 |
-1,11 |
00-10-30 |
3 |
0,00 |
-0,38 |
2,08 |
2,07 |
0,77 |
0,00 |
0,93 |
-0,98 |
-1,11 |
00-10-31 |
4 |
0,00 |
-0,38 |
-1,02 |
1,35 |
0,38 |
6,06 |
0,00 |
-0,99 |
-1,13 |
00-11-02 |
5 |
0,53 |
0,38 |
3,09 |
2,00 |
-2,29 |
2,86 |
-5,50 |
0,00 |
2,50 |
00-11-03 |
6 |
0,27 |
0,76 |
4,67 |
1,31 |
3,12 |
4,17 |
6,80 |
1,99 |
3,52 |
00-11-06 |
7 |
0,53 |
0,38 |
1,27 |
1,94 |
-1,70 |
-9,87 |
-3,64 |
-2,44 |
1,11 |
00-11-07 |
8 |
0,53 |
-0,38 |
1,57 |
0,00 |
0,77 |
2,96 |
0,94 |
-0,50 |
2,24 |
00-11-08 |
9 |
-1,83 |
0,38 |
-0,93 |
-4,43 |
0,38 |
-3,74 |
-1,87 |
0,00 |
-0,91 |
00-11-09 |
10 |
0,00 |
-0,38 |
-1,88 |
-1,99 |
-1,90 |
-4,48 |
0,00 |
1,51 |
-1,57 |
00-11-10 |
11 |
0,00 |
0,00 |
-0,32 |
-2,70 |
-2,91 |
0,00 |
0,00 |
-0,99 |
-1,55 |
00-11-13 |
12 |
0,00 |
0,76 |
-2,56 |
1,39 |
-2,00 |
-1,56 |
0,00 |
-0,50 |
-3,23 |
00-11-14 |
13 |
0,00 |
-0,38 |
1,64 |
-9,59 |
0,00 |
-1,59 |
-2,86 |
0,50 |
1,74 |
00-11-15 |
14 |
1,33 |
0,00 |
1,29 |
6,06 |
1,02 |
5,81 |
4,90 |
1,00 |
1,18 |
00-11-16 |
15 |
0,00 |
0,00 |
-1,59 |
0,00 |
0,00 |
1,22 |
-2,80 |
-1,98 |
-0,86 |
Źródło: opracowanie własne
1.9. Próbkowe oszacowania parametrów rozkładu stóp zwrotu
Na podstawie zaobserwowanych wartości stóp zwrotu możemy wyznaczyć tzw. empiryczne rozkłady stóp zwrotu, oszacować ich parametry oraz ewentualnie zweryfikować hipotezę, czy rozkład empiryczny istotnie różni się od wybranego, znanego rozkładu (np. normalnego).
Istotnym założeniem uzasadniającym wykorzystanie obserwacji historycznych do szacowania parametrów rozkładu stóp zwrotu w okresie przyszłym jest założenie o stałości tych parametrów w czasie. Umożliwia ono potraktowanie historycznych (zaobserwowanych) stóp zwrotu jako równie prawdopodobnych. Zatem każdej historycznej realizacji stopy zwrotu przypisane jest równe prawdopodobieństwo ![]()
. Założenie to może być zaakceptowane zwykle dla niezbyt długich okresów czasu.
Wartość oczekiwana stopy zwrotu ![]()
jest szacowana za pomocą średniej stopy zwrotu z próby historycznej:
![]()
.
Wariancja tej stopy ![]()
jest szacowana za pomocą wariancji z próby:
![]()
natomiast odchylenie standardowe za pomocą odchylenia standardowego z próby:
![]()
.
Semiwariancja z próby określona jest jako:
![]()
gdzie ![]()
oznacza liczbę ujemnych odchyleń od średniej, natomiast
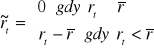
.
Semiodchylenie standardowe z próby będzie wyznaczone jako pierwiastek kwadratowy z semiwariancji, tj:
![]()
.
Empiryczny współczynnik zmienności stopy zwrotu określany jest jako:
![]()
.
Próbkowe oszacowania współczynnika korelacji dla dwóch walorów A i B znajdziemy otrzymamy na podstawie wzoru:
![]()
gdzie ![]()
jest próbkową kowariancją stóp zwrotu.
Oszacowania wymienionych wyżej parametrów rozkładu na podstawie próby 15 obserwacji sesyjnych przedstawiamy w tablicy 9.
Tabela 9. Oszacowania wybranych parametrów rozkładu stóp zwrotu
Parametry |
ragros |
rambank |
ramica |
rampli |
rams |
ranimex |
rapator |
rapexim |
rwig |
|
0,090 |
0,026 |
0,220 |
0,067 |
-0,441 |
-0,075 |
-0,145 |
-0,256 |
-0,012 |
Minimum |
-1,832 |
-0,382 |
-3,030 |
-9,589 |
-2,913 |
-9,867 |
-5,505 |
-2,439 |
-3,230 |
Maksimum |
1,333 |
0,763 |
4,667 |
6,061 |
3,125 |
6,061 |
6,796 |
1,990 |
3,525 |
Rozstęp |
3,166 |
1,145 |
7,697 |
15,650 |
6,038 |
15,927 |
12,301 |
4,429 |
6,754 |
|
0,651 |
0,417 |
2,207 |
3,743 |
1,706 |
4,205 |
3,112 |
1,276 |
1,907 |
|
7,23 |
16,04 |
10,03 |
55,87 |
-3,87 |
-56.07 |
-21,46 |
-4,98 |
-158,92 |
Źródło: opracowanie własne
Macierz oszacowań współczynników korelacji stóp zwrotu ukazuje siłę i kierunek skorelowania poszczególnych par walorów.
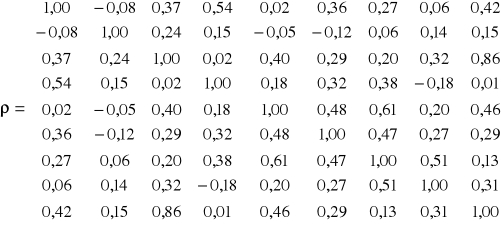
Należy zauważyć, że w rozpatrywanym przykładzie, w większości przypadków korelacja stóp zwrotu była dodatnia, lecz statystycznie nieistotnie różna od zera.
2. Podstawy podejmowania decyzji w warunkach pewności i niepewności
2.1. Wybór w warunkach pewności
Rozważmy sytuację, w której pewna osoba dysponuje, na koniec dwóch kolejnych lat, dochodem realnym równym 21600 złotych. Załóżmy, że dochody te będą uzyskane na pewno. Wprowadźmy oznaczenia:
![]()
- dla dochodu na koniec roku pierwszego,
![]()
- dla dochodu na koniec roku drugiego.
W analizowanym przypadku osoba ta może przeznaczyć dochód na konsumpcję, bądź zrezygnować z niej i przeznaczyć na inwestycję. Załóżmy, że jedyną możliwą inwestycją jest zdeponowanie wolnych środków pieniężnych na rachunku bankowym. Załóżmy nadto, że stopy procentowe w dwóch kolejnych latach nie zmieniają się i wynoszą ![]()
(tj. 8% w stosunku rocznym). Załóżmy także, że stopa procentowa, po której można pożyczyć w banku pieniądze ![]()
jest także równa 8% tj. ![]()
.
Jakie możliwości wyboru ma przed sobą wymieniona osoba i które z nich będą dla niej najlepsze? Odpowiedzi na powyższe pytania będą tematem wykładu. Rozważmy trzy charakterystyczne opcje wyboru.
1. Załóżmy, że rozpatrywana osoba przeznacza na konsumpcję całe dochody, którymi dysponuje. Wprowadzając oznaczenia ![]()
dla konsumpcji w roku t oraz ![]()
dla oszczędności na koniec danego roku otrzymamy:
![]()
, ![]()
, ![]()
, ![]()
.
Na rysunku sytuację tą obrazuje punkt D.
2. Załóżmy, że rozpatrywana osoba rezygnuje całkowicie z konsumpcji w okresie t=1, natomiast zaoszczędzony dochód deponuje na rachunku bankowym. W omawianym przypadku, w roku t=1 otrzymamy: ![]()
, ![]()
. Na koniec kolejnego roku t=2, w wyniku inwestycji, dochód do dyspozycji, który można będzie przeznaczyć na konsumpcję wyniesie:
![]()
, ![]()
.
Widać zatem, że rezygnacja z konsumpcji w okresie t=1 spowodowała zwiększenie możliwości konsumpcyjnych w roku następnym, w wyniku efektu zainwestowania zaoszczędzonego dochodu. Na rysunku sytuację tą obrazuje punkt A.
3. Załóżmy, że rozpatrywana osoba podejmuje decyzję, by skonsumować w okresie t=1 więcej niż wynosi dochód w tym okresie. Maksymalna kwota, jaką może pożyczyć osoba, której dochód w okresie t=2, wyniesie 21600, powinna spełniać równanie: ![]()
, a zatem wartość przyszła pożyczki powinna się równać dochodowi w przyszłym okresie. Stąd otrzymujemy:
![]()
.
W konsekwencji konsumpcja w roku t=1, powiększona o pożyczkę a conto przyszłych dochodów wyniesie: ![]()
. W roku t=1 oszczędności będą ujemne, ponieważ ![]()
, natomiast konsumpcja roku t=2 będzie zerowa ![]()
. Na rysunku sytuację tą obrazuje punkt B.
Wszystkie omówione przypadki szczególne spełniają równanie:
wartość przyszła ciągu konsumpcji = wartość przyszła ciągu dochodów |
lub co na jedno wychodzi:
wartość bieżąca ciągu konsumpcji = wartość bieżąca ciągu dochodów. |
Równania te zapiszemy w sposób formalny jako:
![]()
(w kategoriach wartości przyszłej)
lub
![]()
(w kategoriach wartości bieżącej).
Wszystkie możliwe poziomy konsumpcji w okresach t=1 oraz t=2 są rozwiązaniami pierwszego bądź drugiego równania, a ich obrazy graficzne leżą na odcinku AB zamieszczonym na rysunku 1. Odcinek ten należy do prostej o równaniu:
![]()
lub inaczej
![]()
.
Widzimy zatem, że prosta zapisana wyżej ma ujemny współczynnik kierunkowy, co oznacza ujemną zależność pomiędzy konsumpcją w roku t=1, a konsumpcją w roku następnym. Wzrost konsumpcji w roku t=1 o jednostkę, spowoduje spadek konsumpcji w roku t=2 o wielkość ![]()
. W naszym przypadku otrzymamy, że:
![]()
z czego wynika, że wzrost konsumpcji w roku t=1 o jeden złoty, spowoduje spadek konsumpcji w roku t=2 o 1,08 złotych. Inaczej mówiąc - spadek konsumpcji bieżącej, czyli wzrost inwestycji o jednostkę, spowoduje przyrost konsumpcji przyszłej o 1,08 złotych.
Rysunek 3 przedstawia zbiór rozwiązań dopuszczalnych dla inwestora, który podejmuje decyzje odnośnie do swojej konsumpcji teraźniejszej i przyszłej, w warunkach opisanych w przykładzie. Nie rozwiązana jest jednak kwestia, którą z dopuszczalnych decyzji inwestor wybierze. Aby odpowiedzieć na to pytanie wprowadzimy nieco pojęć, które pozwolą nam zrozumieć podstawy wyboru inwestycyjnego najpierw w warunkach pewności potem zaś w warunkach ryzyka.
Rysunek 3. Możliwości wyboru w warunkach pewności
![]()
44928 A oszczędności
21600 D
kredyt
21600 41600 B ![]()
Źródło: opracowanie własne
Przez inwestowanie będziemy rozumieli, najogólniej rzecz ujmując, powstrzymywanie się od konsumpcji. Inwestowanie ma charakter dynamiczny i umożliwia jednostkom (inwestorom) osiągnięcie w dwóch lub większej liczbie następujących po sobie okresów innych poziomów konsumpcji niż te, które wynikają z uzyskiwanych przez nich w tych okresach dochodów. Inwestycja może mieć charakter zarówno rzeczowy, jak i pieniężny (kapitałowy). W najprostszej sytuacji decyzyjnej (tak jak we wstępnym przykładzie) rozważa się dwa okresy: bieżący i przyszły. Pierwszy nazywa się umownie teraźniejszością, drugi natomiast - przyszłością. Zakłada się, że inwestorzy znają swoje teraźniejsze możliwości inwestowania oraz przyszłe konsekwencje ich przedsięwzięcia oraz nie ponoszą przy tym z tytułu decyzji inwestycyjnych żadnych kosztów, czy to w postaci kosztu zawarcia transakcji, czy też podatków. Każdy z nich dysponuje bieżącym dochodem równym ![]()
oraz dochodem równym ![]()
w przyszłości. Ponadto musi zadecydować o wielkości swojej bieżącej konsumpcji ![]()
oraz o rodzaju przedsięwziętej inwestycji po to, aby w przyszłości osiągnąć konsumpcję równą ![]()
.
Przy podejmowaniu decyzji odnośnie do wielkości konsumpcji w każdym okresie inwestor ujawnia swoje preferencje, które zgodnie z teorią zachowania konsumenta można opisać przy pomocy funkcji użyteczności w postaci:
![]()
.
Funkcja ta jest odwzorowaniem, które każdej kombinacji konsumpcji teraźniejszej ![]()
i przyszłej ![]()
przyporządkowuje pewną wartość liczbową ze zbioru liczb rzeczywistych nieujemnych. Porządkuje ona zbiór wszystkich możliwych kombinacji konsumpcji teraźniejszej i przyszłej w taki sposób, że dla dowolnych dwóch dostępnych inwestorowi kombinacji A i B, prawdziwe są stwierdzenia:
1. Inwestor przedkłada kombinację konsumpcji ![]()
nad kombinację konsumpcji ![]()
wtedy i tylko wtedy, gdy ![]()
.
2. Kombinacja konsumpcji ![]()
satysfakcjonuje inwestora w równym stopniu co kombinacja konsumpcji ![]()
wtedy i tylko wtedy, gdy ![]()
.
O funkcji użyteczności zakłada się , że posiada następujące własności:
1. Jest ciągła i posiada ciągłe pochodne cząstkowe do rzędu drugiego włącznie. Oznacza to - między innymi - doskonałą podzielność dobra konsumowanego w obu okresach (w ujęciu fizycznym lub pieniężnym).
2. ![]()
, co oznacza, że zerowa konsumpcja w dowolnym okresie pociąga za sobą brak satysfakcji inwestora.
3. 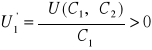
oraz 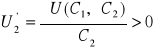
dla dostatecznie dużego przedziału zmienności konsumpcji w obu okresach. Oznacza to z kolei, że użyteczność krańcowa konsumpcji teraźniejszej i przyszłej jest dodatnia. Zatem jednostkowy przyrost konsumpcji w jednym okresie przy jej ustalonym poziomie w drugim okresie powoduje przyrost zadowolenia inwestora o wielkość równą krańcowej użyteczności.
4. 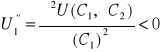
oraz 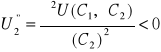
. Użyteczność krańcowa konsumpcji w każdym okresie jest malejąca. Kolejne, równe co do wielkości przyrosty konsumpcji powodują w każdym okresie coraz mniejsze przyrosty zadowolenia inwestora.
Dowolnie ustalony poziom zadowolenia, na przykład ![]()
, może być osiągnięty przez nieskończenie dużą liczbę kombinacji konsumpcyjnych (ze względu na ciągłość funkcji użyteczności) spełniających tożsamość:
![]()
,
w której ![]()
jest przyrostem użyteczności wywołanym przyrostem konsumpcji w każdym z okresów o odpowiednio ![]()
(i=1,2). Kombinacje te tworzą takie pary konsumpcji teraźniejszej i przyszłej, dla których krańcowa stopa substytucji pomiędzy nimi ![]()
jest równa odwrotności ich krańcowych użyteczności:
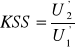
.
Krańcowa stopa substytucji, zdefiniowana powyżej, informuje o liczbie jednostek konsumpcji bieżącej, które musi poświęcić inwestor chcąc zwiększyć konsumpcję przyszłą o jednostkę przy tym samym poziomie zadowolenia.
Zdefiniowanie parametru ![]()
umożliwia przedstawienie liniowej zależności pomiędzy przyrostami konsumpcji w rozpatrywanych okresach. Możemy zapisać, że:
![]()
.
Obrazem graficznym funkcji jednakowej użyteczności jest krzywa obojętności pomiędzy teraźniejszą i przyszłą konsumpcją inwestora. Na krzywej obojętności znajdują się punkty odpowiadające kombinacjom konsumpcji bieżącej i przyszłej dające ten sam poziomach zadowolenia. Krzywe obojętności dla poziomów zadowolenia ![]()
przedstawia rysunek 4.
Rysunek 4. Funkcje obojętności
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Źródło: opracowanie własne
Wróćmy obecnie do rozpatrywanego na początku przykładu inwestora podejmującego decyzje odnośnie do przeznaczenia swoich dochodów (bieżących i przyszłych) na konsumpcję. Zakładać będziemy, że inwestor wybierać będzie, spośród możliwych (dopuszczalnych) kombinacji konsumpcji bieżącej i przyszłej takie, dla których funkcja użyteczności osiągnie wartość największą.
Formalnie zatem opiszemy sytuację decyzyjną (w warunkach pewności) za pomocą modelu:
![]()
przy warunkach: ![]()
; ![]()
; ![]()
.
Inwestor wybierze zatem taką kombinację konsumpcji bieżącej i przyszłej, która jest dopuszczalna (tj. spełnia warunki ograniczające) oraz maksymalizuje funkcję celu. Na rysunku 3 pokazano zbiór rozwiązań dopuszczalnych, tj. odcinek AB, należący do prostej ![]()
. Z drugiej strony na rysunku 4 przedstawiono krzywe obojętności, charakteryzujące kombinacje konsumpcji bieżącej i przyszłej, które dają taki sam poziom zadowolenia. Możemy pokazać, że inwestor wybierze taki punkt na odcinku AB, który będzie dawał największą wartość funkcji użyteczności. Pokazujemy to na rysunku 5.
Z rysunku 5 widać, że inwestor charakteryzujący się taką funkcją obojętności (krzywizna tej funkcji zależy od wartości współczynnika krańcowej stopy substytucji pomiędzy konsumpcją bieżącą i przyszłą), wybierze punkt W należący do odcinka AB, a więc punkt styczności prostej wyznaczającej ograniczenia budżetowe konsumpcji z krzywą obojętności. Inwestor w rozpatrywanych warunkach nie może uzyskać wyższego poziomu użyteczności niż U1. Zauważmy, że krzywa U0, definiująca niższą niż U1 wartość użyteczności przecina odcinek AB w innych punktach niż W. Zatem w każdym innym iż W punkcie zbioru rozwiązań dopuszczalnych użyteczność jest mniejsza niż w punkcie styczności. Przykładowe krzywe U2 i U3 definiują kombinacje konsumpcji dające użyteczności większe niż U1, jednak te kombinacje konsumpcji nie spełniają warunku budżetowego (są niedopuszczalne).
Rysunek 5. Wybór kombinacji konsumpcji bieżącej i przyszłej, dający maksimum funkcji użyteczności
![]()
44928 A
W
21600 D
U3
U2
U1
U0
21600 41600 B ![]()
Źródło: opracowanie własne
Do tej pory mówiliśmy o funkcji użyteczności określonej na poziomach konsumpcji bieżącej i przyszłej. W przypadku, gdy rozpatrujemy dochody (konsumpcję) w wielu kolejnych okresach czasu wygodniej jest wprowadzić pojęcie dochodu skapitalizowanego (konsumpcji skapitalizowanej). Niech stopa dyskontowa będzie równa ![]()
. Wtedy skapitalizowanym dochodem ![]()
, wyrażonym w kategoriach wartości przyszłej będzie:
![]()
.
Dochód taki nazywać będziemy bogactwem (zamożnością inwestora). W większości przypadków problem podejmowania decyzji inwestycyjnych rozpatrywać będziemy w kategoriach funkcji użyteczności bogactwa (zamożności) inwestora. Określimy zatem funkcję:
![]()
,
którą nazywać będziemy funkcją użyteczności bogactwa. W warunkach, gdy dochody w poszczególnych okresach czasu byłyby pewne, mówilibyśmy o wyborze w warunkach pewności. Podobnie jak poprzednio zakładać będziemy, że inwestor dąży do maksymalizacji funkcji użyteczności bogactwa:
![]()
przy warunku budżetowym, że skapitalizowany dochód równa się skapitalizowanej konsumpcji.
O funkcji użyteczności bogactwa zakładać będziemy, że posiada następujące własności, które charakteryzować będą tzw. inwestora niechętnego wobec ryzyka:
1. Jest ciągła i posiada ciągłe pochodne cząstkowe do rzędu drugiego włącznie.
2. ![]()
, co oznacza, że zerowe bogactwo pociąga za sobą brak satysfakcji inwestora.
3. ![]()
dla dostatecznie dużego przedziału zmienności bogactwa. Oznacza, że użyteczność krańcowa bogactwa jest dodatnia. Przyrost zamożności o jednostkę, powoduje wzrost użyteczności (zadowolenia) o wielkość równą krańcowej użyteczności.
4. 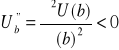
- użyteczność krańcowa bogactwa jest malejąca. Kolejne, równe co do wielkości przyrosty bogactwa, powodują w każdym okresie coraz mniejsze przyrosty zadowolenia inwestora.
Rysunek 6. Funkcje użyteczności bogactwa inwestora
(c)
U(b) (b)
(a)
b
Źródło: opracowanie własne
Wykres wklęsłej funkcji użyteczności bogactwa o własnościach 1-4 przedstawia krzywa (a) na rysunku 6. Na rysunku 6 ukazano jeszcze dwie inne krzywe użyteczności (b) i (c), które charakteryzować będą tzw. inwestora obojętnego wobec ryzyka i inwestora lubiącego ryzyko. W obu przypadkach, tak jak w przypadku funkcji użyteczności (a) dla inwestora niechętnego wobec ryzyka, funkcje użyteczności są rosnące względem bogactwa ![]()
. Jednakże dla inwestora obojętnego wobec ryzyka 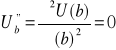
tj. użyteczność krańcowa nie zmienia się wraz ze wzrostem bogactwa, natomiast dla inwestora lubiącego ryzyko 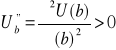
, tj. użyteczność krańcowa rośnie w miarę wzrostu bogactwa.
2.2. Wybór w warunkach ryzyka
W świecie realnym inwestor nie posiada pełnej wiedzy i pełnej władzy odnośnie do warunków podejmowanych przez siebie decyzji. Decyzje te bowiem skutkują niepewnymi wynikami w przyszłości. Inwestor może co najwyżej określić zbiór możliwych wyników oraz określić prawdopodobieństwo ich realizacji. Inwestor może zatem oczekiwać określonego przez siebie wyniku swoich decyzji, jednakże wynik zrealizowany będzie, w ogólnym przypadku, inny niż wynik oczekiwany. W konsekwencji inwestor nie jest pewny efektu podjętego działania - skapitalizowanego na dowolny moment czasowy poziomu swojego bogactwa. Zna on jedynie rozkład możliwych do osiągnięcia poziomów bogactwa i w konsekwencji zna rozkład prawdopodobieństwa swojego zadowolenia z osiągniętego poziomu bogactwa. Zatem jeżeli ![]()
jest zmienną losową o znanym rozkładzie, to inwestor dążyć będzie do maksymalizacji oczekiwanej użyteczności swojego bogactwa, co zapiszemy:
![]()
.
Rozpatrzmy najprostszy przypadek podejmowania decyzji w warunkach niepewności (ryzyka) wyjaśniając przy tym pojęcie niechęci wobec ryzyka. Rozważmy raz jeszcze inwestora, który charakteryzuje się funkcją użyteczności o własnościach takich, jak opisano w punkcie poprzednim, tj. funkcją rosnącą coraz wolniej w zależności w miarę wzrostu poziomu bogactwa (zobacz rysunek 7).
Dla inwestora charakteryzującego się taką funkcją użyteczności rozpatrzmy dwie inwestycje:
1) inwestycja przynosząca pewny skapitalizowany dochód w wysokości ![]()
, której odpowiada pewny poziom użyteczności równy ![]()
, co zapiszemy formalnie (zobacz rysunek 7):
![]()
![]()
![]()
,
2) inwestycja w warunkach ryzyka, przynosząca taki sam oczekiwany dochód jak inwestycja pewna (zobacz rysunek 7). Zakładamy, że mogą wystąpić dwa wyniki inwestycji z równym prawdopodobieństwem. Jeden gorszy, dający ![]()
i drugi lepszy dający ![]()
. Zakładamy ponadto, że ![]()
; ![]()
oraz ![]()
, tzn. że wyniki ,,lepszy'' i ,,gorszy'' leżą symetrycznie względem wyniku pewnej inwestycji równego ![]()
. W takim przypadku zachodzi:
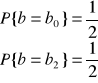
![]()
![]()
.
Zatem oczekiwany dochód równa się dochodowi, który można uzyskać nie podejmując ryzyka. W takim też przypadku możemy określić oczekiwaną użyteczność inwestycji ryzykownej. Ponieważ :
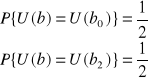
![]()
![]()
.
Możemy pokazać, z uwagi na własności funkcji użyteczności, rosnącej coraz wolniej, że:
![]()
![]()
![]()
.
Rysunek 7. Funkcja użyteczności bogactwa inwestora niechętnego wobec ryzyka
U(b)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
b
Źródło: opracowanie własne
W konsekwencji możemy udowodnić, że:
![]()
,
tzn. oczekiwana użyteczność inwestycji ryzykownej, dającej ten sam oczekiwany dochód, co inwestycja pewna, jest mniejsza niż użyteczność dochodu pewnego. Nierówność ta jest konsekwencją niesymetryczności funkcji użyteczności (rosnącej coraz wolniej dla coraz większych poziomów dochodów). Mamy bowiem:
![]()
.
Ponieważ ![]()
, zatem prawdą jest, że ![]()
.
Istota niechęci do ryzyka może być wyrażona w następujący sposób: oczekiwana użyteczność z ryzykownej inwestycji, przynoszącej taki sam oczekiwany dochód, jak inwestycja pewna, będzie zawsze mniejsza, niż użyteczność tego samego bogactwa w warunkach pewności, zakładając, że inwestor jest niechętny ryzyku . Wynika stąd , że inwestor niechętny ryzyku, nie wybierze ryzykownej inwestycji dającej taki sam oczekiwany dochód jak inwestycja pewna.
Dla inwestora niechętnego wobec ryzyka można wyznaczyć dochód ekwiwalentny (ekwiwalent pewności), oznaczony ![]()
, który zapewnia użyteczność równą oczekiwanej użyteczności uzyskanej w warunkach podjęcia inwestycji ryzykownej. Zatem:
![]()
.
Ponieważ dla inwestora niechętnego wobec ryzyka zachodzi ![]()
, zatem mniejszy dochód, ale uzyskany na pewno, generuje taką samą użyteczność jak oczekiwana użyteczność z inwestycji ryzykownej. Inaczej mówiąc, różnica ![]()
, nazywana premią za ryzyko, określa wielkość dochodu z jakiego inwestor niechętny wobec ryzyka gotów jest zrezygnować, by nie podejmować ryzyka.
Dla inwestora obojętnego wobec ryzyka, dla którego funkcja użyteczności bogactwa jest linią prostą, krańcowa użyteczność bogactwa jest stała. Zatem dla takiego inwestora zachodzi:
![]()
![]()
![]()
![]()
![]()
.
Dla takiego inwestora premia za ryzyko wynosi zero![]()
.
Dla inwestora lubiącego ryzyko, dla którego funkcja użyteczności bogactwa rosnąca coraz bardziej w miarę wzrostu bogactwa, krańcowa użyteczność bogactwa jest rosnąca. Zatem dla takiego inwestora zachodzi:
![]()
![]()
![]()
![]()
![]()
.
2.3. Funkcja użyteczności stopy zysku
W rozważaniach dotyczących wyboru w warunkach ryzyka częściej wykorzystywana jest oczekiwana funkcja użyteczności stopy zwrotu bogactwa. Zdefiniujmy stopę zwrotu bogactwa jako:
![]()
.
W warunkach ryzyka stopa zwrotu jest zmienną losową, której rozkład scharakteryzować możemy za pomocą m.in. oczekiwanej stopy zwrotu ![]()
oraz wariancji stopy zwrotu ![]()
.
Zakładać będziemy, ze inwestor dążyć będzie do maksymalizacji funkcji oczekiwanej użyteczności stopy zwrotu bogactwa, tj.:
![]()
.
Rozwijając oczekiwaną użyteczność stopy zwrotu, wokół oczekiwanej stopy zwrotu, w szereg Taylora otrzymamy:
![]()
.
Aby nie komplikować wykładu od strony matematycznej nie pokazujemy dokładnie postaci funkcji ![]()
. Można wykazać, że dla inwestora niechętnego wobec ryzyka funkcja ta jest rosnąca względem oczekiwanego dochodu i malejąca względem ryzyka (mierzonego wariancją stopy zwrotu), tzn.:
![]()
; 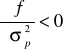
,
oznacza to, że wzrost oczekiwanego zysku z inwestycji, przy ustalonym ryzyku przyczynia się do wzrostu oczekiwanej użyteczności, natomiast wzrost ryzyka inwestycji, przy ustalonym oczekiwanym dochodzie będzie skutkował spadkiem użyteczności.
Inwestor dążący do maksymalizacji oczekiwanej funkcji użyteczności stopy zwrotu będzie zatem podejmował decyzje inwestycyjne biorąc pod uwagę dwa parametry: oczekiwany zysk i ryzyko. W szczególności dla założonego poziomu ryzyka będzie wybierał inwestycję oferującą jak największy oczekiwany zysk oraz dla założonego poziomu oczekiwanego dochodu będzie wybierał inwestycję charakteryzującą się najmniejszym ryzykiem. Dwuargumentowa funkcja ![]()
ukazuje, że te same wartości oczekiwanej użyteczności inwestor może uzyskać wybierając inwestycje charakteryzujące się różnymi poziomami oczekiwanego zysku i ryzyka. Posługując się przedstawioną wyżej funkcją oczekiwanej użyteczności wyznaczmy krzywe obojętności, zatem takie krzywe w przestrzeni ,,ryzyko; dochód'', tj. ![]()
, które wyznaczają stałe oczekiwane użyteczności.
Załóżmy, że inwestor chce osiągnąć poziom oczekiwanej użyteczności równy ![]()
. Rozwiążmy zatem równanie ![]()
. W tym celu obliczymy różniczkę zupełną funkcji dwóch argumentów: oczekiwanego zysku ![]()
oraz ryzyka ![]()
w punkcie dającym zakładaną wartość oczekiwanej użyteczności. Różniczka zupełna, będąca sumą różniczek cząstkowych względem ![]()
oraz ![]()
, dla zapewnienia ustalonej wielkości oczekiwanej użyteczności, może być zapisana następująco:
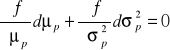
,
gdzie ![]()
jest przyrostem oczekiwanego zysku, natomiast ![]()
jest przyrostem ryzyka.
Rozwiązując zapisane wyżej równanie otrzymujemy współczynnik, który oznaczymy ![]()
i nazywać będziemy absolutnym współczynnikiem niechęci do ryzyka. Współczynnik ten ma postać:
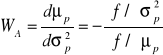
,
i umożliwia zapisanie liniowej zależności pomiędzy przyrostem oczekiwanego zysku i przyrostem ryzyka w postaci:
![]()
.
Jakie wartości może przyjmować współczynnik ![]()
, w przypadku, gdy inwestor jest niechętny wobec ryzyka (ma funkcję użyteczności wklęsłą)? Ponieważ dla inwestora niechętnego wobec ryzyka krańcowa użyteczność oczekiwanej stopy zwrotu jest dodatnia ![]()
, natomiast krańcowa użyteczność względem wariancji jest ujemna ![]()
, zatem współczynnik absolutnej niechęci do ryzyka jest dodatni ![]()
. Wartość współczynnika niechęci wobec ryzyka decyduje o stopniu niechęci wobec ryzyka. Wynika to z interpretacji tego współczynnika jako przyrostu oczekiwanego zysku przypadającego na jednostkę przyrostu ryzyka (mierzonego wariancją stopy zwrotu). Większa wartość współczynnika niechęci wobec ryzyka oznacza, że inwestor musi uzyskać większy przyrost oczekiwanej wartości portfela w zamian za podjęcie dodatkowego ryzyka, aby zachować taki sam poziom użyteczności. Rozważmy dwóch inwestorów, z których jeden charakteryzuje się współczynnikiem niechęci do ryzyka równym np. ![]()
, natomiast drugi współczynnikiem ![]()
. W pierwszym przypadku, dla zachowania tego samego poziomu użyteczności, wzrostowi ryzyka o jednostkę towarzyszyć musi wzrost oczekiwanego zysku z inwestycji o 2 jednostki. Zatem wszystkie inwestycje dające mniejsze przyrosty oczekiwanych zysków niż 2 na jednostkę ryzyka, będą odrzucane przez inwestora niechętnego wobec ryzyka. W drugim przypadku, dla zachowania tego samego poziomu użyteczności, wzrostowi ryzyka o jednostkę towarzyszyć musi wzrost oczekiwanego zysku z inwestycji o 0,2 jednostki. Widzimy, że drugi inwestor wykazuje większą tolerancję wobec ryzyka.
Jeśli scałkujemy zapisane wyżej wyrażenie otrzymamy zbiór liniowych zależności pomiędzy oczekiwanym zyskiem a ryzykiem, zapewniający uzyskanie założonego (dowolnego) poziomu oczekiwanej użyteczności ![]()
:
![]()
.
Równanie to definiuje zlinearyzowany zbiór krzywych obojętności w przestrzeni ,,ryzyko; dochód''. Dla różnych poziomów oczekiwanej użyteczności ![]()
otrzymujemy zbiór prostych o tym samym współczynniku kierunkowym ![]()
. Pokazuje to rysunek 8.
Rysunek 8. Zlinearyzowane krzywe obojętności w przestrzeni wartość oczekiwana - wariancja.
![]()
(a)
(b)
(c)
![]()
Źródło: opracowanie własne
Na rysunku 8 przedstawiono trzy proste równoległe (o takim samym współczynniku kierunkowym), jednakże zapewniające uzyskanie różnych poziomów oczekiwanej użyteczności:
(a) ![]()
,
(b) ![]()
,
(c) ![]()
,
przy czym ![]()
.
Z drugiej strony, każdy punkt na prostej (a) definiuje różne inwestycje (o różnym ryzyku i dochodzie) jednakże dające ten sam poziom użyteczności ![]()
.
Rysunek 9. Krzywe obojętności w przestrzeni wartość oczekiwana - odchylenie standardowe
![]()
(a)
(b)
(c)
![]()
Źródło: opracowanie własne
Rysunek 10. Zlinearyzowane krzywe obojętności w przestrzeni wartość oczekiwana - wariancja.
![]()
(a)
(b)
![]()
![]()
Źródło: opracowanie własne
Kolejny rysunek 9 pokazuje krzywe obojętności w przestrzeni wartość oczekiwana - odchylenie standardowe ![]()
. Krzywe te nie są już prostymi. Są one wypukłe. Zatem wklęsłe funkcje użyteczności prowadzą do wypukłych funkcji obojętności. Z rysunków tych wynika także, iż poziom oczekiwanej użyteczności mierzony jest za pomocą oczekiwanej stopy zwrotu portfela, gdy wariancja portfela (odchylenie standardowe) jest równa zero, tj. gdy nie występuje ryzyko.
Jak pokazaliśmy, współczynnik ![]()
absolutnej niechęci do ryzyka jest współczynnikiem kierunkowym prostych określających zależności między oczekiwaną stopą zwrotu ![]()
a wariancją portfela ![]()
. Od wielkości tego współczynnika zależy zatem wypukłość krzywych obojętności pokazanych w przestrzeni ![]()
. Im większą wartość osiągnie współczynnik ![]()
tym nachylenie prostej ![]()
będzie większe, tym większa będzie wypukłość krzywych obojętności na rysunku 9. Większa stromość krzywych obojętności (gdy ![]()
jest duże) oznacza, że inwestor musi uzyskać większy przyrost oczekiwanej wartości portfela w zamian za podjęcie dodatkowego ryzyka. Pokazuje to rysunek 10. Przedstawiono na nim dwie proste, dla różnych stopni niechęci wobec ryzyka. Widać, że dla prostej (a) konieczny przyrost wartości oczekiwanej portfela, by skompensować ten sam przyrost ryzyka jest większy niż w przypadku prostej (b).
3. Portfel składający się z dwóch walorów
Na portfel inwestycyjny składają się dostępne na rynku walory, różniące się płynnością, oczekiwanym dochodem i ryzykiem, które inwestor może uwzględnić w swoich decyzjach inwestycyjnych. Struktura portfela musi być dostosowana do potrzeb inwestora. Musi zatem uwzględniać jego indywidualne cechy osobowe, jego sytuację ekonomiczną oraz horyzont czasowy inwestycji. Określenie tych cech stanowi punkt wyjścia do wyznaczenia i zhierarchizowania celów inwestowania. Dopiero wtedy, gdy rozstrzygnięte zostaną powyższe, z natury jakościowe problemy, jest miejsce na stosowanie sformalizowanych, matematycznych metod analizy portfelowej.
3.1. Wagi portfelowe
Załóżmy, że inwestor dysponuje kwotą ![]()
zł, którą zamierza zainwestować w ryzykowne walory (np. akcje zwykłe) oraz, że przeznacza on kwotę ![]()
zł na zakup waloru A, natomiast pozostałą kwotę tj., ![]()
zł na zakup waloru B. Zatem:
![]()
.
Dzieląc obie strony powyższej równości przez F otrzymamy:
![]()
.
Współczynniki:
![]()
, ![]()
określające, jaka część ogólnego funduszu jest przeznaczona na zakup poszczególnych walorów, nazywać będziemy wagami portfelowymi. W rozpatrywanym przykładzie tak określone wagi wynoszą: ![]()
,![]()
i spełniają:
![]()
; ![]()
; ![]()
.
Wagi określają więc strukturę portfela.
Dla dowolnej liczby walorów, np. K, możemy zapisać:
![]()
; ![]()
; ![]()
; ![]()
.
W ogólnym przypadku wagi portfelowe mogą być dodatnie lub ujemne. Ogólna definicja wagi portfelowej stanowi bowiem, że:
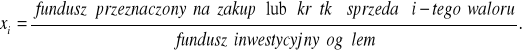
Dodatnia waga portfelowa ![]()
oznacza, że inwestor zakupuje walor A. Czynność tę nazywamy inaczej zajmowaniem tzw. długiej pozycji na rynku waloru A. Możliwe jest także zajęcie przez inwestora tzw. krótkiej pozycji lub dokonanie tzw. krótkiej sprzedaży waloru A. Wtedy waga portfelowa dla tego waloru jest ujemna.
Krótka sprzedaż nie jest sprzedażą waloru, który się posiada, lecz sprzedażą waloru, którego się nie posiada. Załóżmy, że inwestor pożycza od kogoś, zwykle przez pośrednika, 100 akcji firmy B. Inwestor zobowiązuje się zwrócić po pewnym okresie tych 100 akcji osobie, od której pożyczył. Licząc na to, że akcje B spadną sprzedaje je po cenie bieżącej, np. 10 złotych, zarabiając 1 tys. złotych. Po pewnym czasie cena B spada do 5 złotych. Zatem inwestor wraca na rynek i kupuje 100 akcji B, które musi oddać, płacąc za nie 500 złotych (a nie za 1 tys. zł, jak poprzednio). Inwestor zwraca osobie, od której pożyczył owe 100 akcji i w ten sposób krótka sprzedaż zostaje zakończona. Inwestor zyskuje na tej operacji 500zł. Jeśli w czasie trwania krótkiej sprzedaży zostanie wypłacona dywidenda, inwestor musi ją zwrócić właścicielowi.
Wyjaśnijmy teraz, jak wyglądają wagi portfelowe, gdy suma uzyskana w wyniku przeprowadzenia krótkiej sprzedaży waloru B jest przeznaczona na dodatkowy zakup waloru A.
Załóżmy, że inwestor ma ![]()
zł własnych pieniędzy (jego fundusz inwestycyjny), które inwestuje w walory A i B. Załóżmy, że sprzedaje on krótko akcje B za 100zł i wykorzystuje tę kwotę na dodatkową inwestycję w walor A. Zatem kupuje akcje A za ![]()
zł. Waga portfelowa waloru A wynosi więc:
![]()
,
natomiast waga dla waloru B wynosi
![]()
ponieważ akcje B musimy odkupić i zwrócić. Waga portfelowa jest w tym przypadku ujemna. W dalszym ciągu jednak wagi sumują się do jedności
![]()
.
Szczególnym przypadkiem jest portfel, w tworzeniu którego nie są angażowane własne środki inwestora, lecz tylko środki pochodzące z krótkiej sprzedaży. W takim przypadku suma wag portfelowych jest równa zero.
Załóżmy, że inwestor nie posiada własnych środków ![]()
zł. Załóżmy, że sprzedaje on krótko akcje B za 100 zł i wykorzystuje tę kwotę na dodatkową inwestycję w walor A. Zatem kupuje akcje A za ![]()
zł. Waga portfelowa waloru A wynosi więc:
![]()
,
natomiast waga dla waloru B wynosi:
![]()
,
ponieważ akcje B musimy odkupić i zwrócić. W tym przypadku wagi sumują się do zera ![]()
.
3.2. Parametry rozkładu portfela
Rozpatrzmy portfel dwuskładnikowy, zawierający walory A i B. Stopy zwrotu tych walorów oraz parametry ich rozkładów (oczekiwaną stopę zwrotu, wariancję stopy zwrotu, odchylenie standardowe stopy zwrotu) oznaczmy:
![]()
, ![]()
, ![]()
, ![]()
dla waloru A oraz
![]()
, ![]()
, ![]()
, ![]()
dla waloru B.
Statystyczną współzależność obu stóp zwrotu mierzy, bądź kowariancja
![]()
,
bądź współczynnik korelacji (liniowej)
![]()
.
Przypomnijmy, że współczynnik korelacji mierzy siłę i kierunek zależności statystycznej między stopą zwrotu jednego i drugiego waloru oraz spełnia ![]()
.
Stopa zwrotu portfela dwuskładnikowego ![]()
jest kombinacją liniową stóp zwrotu walorów wchodzących do portfela. Zatem:
![]()
.
W sytuacji, w której krótka sprzedaż występuje, możliwe jest uzyskanie portfela dającego oczekiwaną stopę zwrotu większą, niż maksymalna stopa zwrotu walorów tworzących portfel.
Wartość oczekiwana stopy zwrotu portfela dwuskładnikowego ![]()
jest kombinacją liniową wartości oczekiwanych stóp zwrotu walorów tworzących portfel. Zatem:
![]()
.
Jeżeli krótka sprzedaż nie występuje, czyli ![]()
, ![]()
, to oczekiwana stopa zwrotu portfela nie może być większa od większej z oczekiwanych stóp ![]()
, ![]()
, ani też nie może być mniejsza od mniejszej z nich. Zatem jeśli ![]()
, to ![]()
.
Załóżmy, że oczekiwane wartości stopy zwrotu walorów A i B wynoszą odpowiednio ![]()
i ![]()
. Jaka będzie oczekiwana stopa zwrotu portfela równomiernego? W portfelu równomiernym wagi portfelowe są równe, zatem ![]()
. Wartością oczekiwaną stopy zwrotu portfela jest zatem:
![]()
.
Jeśli krótka sprzedaż nie występuje, oczekiwana stopa zwrotu portfela nie przekroczy (w naszym przykładzie) 7%, ani też nie będzie mniejsza niż ![]()
. Konstruując portfel papierów wartościowych (bez krótkiej sprzedaży) nie możemy zatem oczekiwać dodatkowych zysków, ponad zysk najbardziej efektywnego składnika tego portfela. Jest tak dlatego, gdyż zarówno stopa zwrotu portfela jak i oczekiwana stopa zwrotu portfela są liniowymi kombinacjami odpowiednich składowych portfela.
Efekt portfelowy - jest efektem wynikającym ze złączenia różnych walorów ryzykownych. Polega on na zmniejszeniu ryzyka portfela w stosunku do ryzyka będącego kombinacją liniową ryzyka poszczególnych walorów. Miarą ryzyka jest odchylenie standardowe stopy zwrotu.
Zdefiniujmy ryzyko ważone będące kombinacją liniową ryzyka poszczególnych walorów jako:
![]()
.
Pokażemy, że ryzyko portfela jest mniejsze lub równe tej wielkości. Wariancją stopy zwrotu portfela dwuskładnikowego jest:
![]()
.
Ponieważ ![]()
, zatem ostateczny wzór na wariancję stopy zwrotu portfela zapiszemy jako
![]()
Wariancja stopy zwrotu portfela zawiera więc składowe będące funkcją wariancji poszczególnych walorów (dwa pierwsze składniki sumy) oraz składnik będący funkcją współczynnika korelacji pomiędzy poszczególnymi stopami zwrotu.
Ryzyko portfela = ryzyko wariancyjne + ryzyko kowariancyjne |
Ryzyko wariancyjne jest ważoną sumą ryzyk składowych portfela. Każdy walor wnosi do portfela swoje indywidualne ryzyko, przy czym udział tego ryzyka w ryzyku portfelowym zależy od kwadratu odpowiedniej wagi portfelowej. Ryzyko kowariancyjne jest natomiast funkcją współczynnika korelacji pomiędzy stopami zwrotu walorów składających się na portfel, tj. ![]()
. Ten właśnie składnik powoduje, że możliwy jest efekt zmniejszenia wariancji portfela. W kolejnym punkcie uzasadnimy to stwierdzenie. Jednakże najpierw zdefiniujmy odchylenie standardowe stopy zwrotu - miernik ryzyka portfelowego. Możemy zapisać że:
![]()
.
Jest zrozumiałe, że miernik ten określa o ile procent (![]()
) realizacje stopy zwrotu portfela odchylają się od oczekiwanej stopy zwrotu portfela.
3.3. Ryzyko portfela, gdy ![]()
Współczynnik korelacji pomiędzy stopami zwrotu może osiągnąć największą wartość, równą jedności ![]()
. W takim przypadku stopy zwrotu obu walorów ,,zmieniają się tak samo''. Wariancja portfela jest w tej sytuacji równa:
![]()
.
W konsekwencji, ryzyko portfela jest ważoną sumą ryzyk związanych z inwestowaniem w akcje A i B, czyli:
![]()
Rozpatrzmy dwa walory charakteryzujące się zadanymi w tablicy 10 parametrami rozkładów ich stóp zwrotu. W kolejnych tablicach przedstawiać będziemy obliczenia dotyczące parametrów rozkładu portfeli utworzonych z waloru A i z waloru B, przy różnym współczynniku korelacji pomiędzy stopami zwrotu obu walorów. W ostatnim wierszu tablicy 10 wymieniono wartości współczynnika korelacji, dla których przedstawione zostaną obliczenia.
Tablica 10. Parametry rozkładu stóp zwrotu walorów tworzących portfel
Walor A |
Walor B |
||
|
|
|
|
3 |
25 |
7 |
64 |
|
|||
Źródło: opracowanie własne
W tablicy 11 pokazano wyliczone wartości oczekiwanych stóp zwrotu portfela oraz błędów standardowych przykładowych portfeli w zależności od wag portfelowych (bez możliwości krótkiej sprzedaży). Można pokazać, że występuje tutaj liniowa zależność pomiędzy wartością oczekiwaną a odchyleniem standardowym stopy zwrotu portfela. Zależność tę wyznaczymy na podstawie następującego układu równań:
![]()
![]()
.
Tablica 11. Parametry rozkładu portfela, gdy ![]()
|
|
|
|
|
2,67 |
-1,67 |
-3,68 |
0,00 |
0,00 |
1,5 |
-0,5 |
1,00 |
12,25 |
3,50 |
1,2 |
-0,2 |
2,20 |
19,36 |
4,40 |
1,0 |
0,0 |
3,00 |
25,00 |
5,00 |
0,8 |
0,2 |
3,80 |
31,36 |
5,60 |
0,5 |
0,5 |
5,00 |
42,25 |
6,50 |
0,2 |
0,8 |
6,20 |
54,76 |
7,40 |
0,0 |
1,0 |
7,00 |
64,00 |
8,00 |
-0,2 |
1,2 |
7,80 |
73,96 |
8,60 |
-0,5 |
1,5 |
9,00 |
90,25 |
9,50 |
Źródło: opracowanie własne
Wyznaczając z drugiego równania ![]()
, przy założeniu, że ![]()
, oraz wstawiając do równania drugiego, otrzymamy:
![]()
.
Wykorzystując dane zawarte w tablicy 10 obliczymy, że:
![]()
.
Zatem, w naszym przykładzie, każdemu wzrostowi ryzyka o jednostkę, czyli wzrostowi odchylenia standardowego portfela o jeden procent, towarzyszy wzrost oczekiwanej stopy zwrotu portfela o 4/3 procent.
Jeśli portfel zawiera tylko walor A lub tylko walor B, wtedy parametry portfela są takie same jak parametry waloru, którego udział w portfelu jest równy 100%. Zinterpretujemy obecnie parametry rozkładu stopy zwrotu przykładowego portfela, dla którego wagi portfelowe równają się ![]()
, ![]()
. Portfel ten powstaje poprzez zainwestowanie ![]()
posiadanego funduszu w zakup walor A oraz zainwestowanie ![]()
funduszu w zakup waloru B. W takim przypadku oczekiwana stopa zysku tak skonstruowanego portfela wyniesie:
![]()
,
natomiast ryzyko mierzone odchylenie standardowym stop zwrotu:
![]()
.
Wnioskujemy stąd, że inwestor może oczekiwać zysku ze wspomnianej inwestycji rzędu ![]()
, przy czym zysk zrealizowany odchylać się może od oczekiwanego in plus in minus o ![]()
.
Jeśli założymy możliwość krótkiej sprzedaży waloru B lub A wówczas nasze wnioski ulegną zmianie. W tablicy 11 przedstawiamy wyniki obliczeń uzyskanych przy takim założeniu (wiersze zacieniowane).
W trzech pierwszych wierszach tej tablicy zapisano wyniki obliczeń w sytuacji, w której inwestor zajmuje krótką pozycję w stosunku do waloru B, a uzyskaną w trakcie krótkiej sprzedaży kwotę przeznacza na dodatkową inwestycję w walor A. Zapewnia mu to niższą oczekiwaną stopę zwrotu portfela (niższą niż stopa zwrotu dla A i dla B), lecz jednocześnie niższe ryzyko portfela (niższe niż ![]()
lub ![]()
). W dwóch ostatnich wierszach tej tablicy zapisano natomiast wyniki obliczeń w sytuacji, w której sprzedajemy krótko walor A i uzyskaną kwotę lokujemy dodatkowo w B. Daje nam to wyższe wartości oczekiwane portfela lecz także wyższe ryzyko. Wykorzystując krótką sprzedaż możemy skonstruować portfel zawierający walory dwa ryzykowne walory A i B i pozbawiony ryzyka. Parametry tego portfela znajdziemy rozwiązując równanie:
![]()
.
Ponieważ ![]()
, zatem:
![]()
.
W konsekwencji wagi portfelowe zapewniające zerowe ryzyko portfela zapiszemy jako:
![]()
; ![]()
.
Waga waloru wchodzącego w skład portfela bez ryzyka, gdy współczynnik korelacji jest równy jedności, zależy od ryzyka drugiego waloru. Waga waloru A będzie ujemna, zaś waloru B dodatnia, gdy ![]()
i odwrotnie - waga waloru A będzie dodatnia, zaś waloru B ujemna, gdy ![]()
.
W przykładzie rozpatrywanym w tablicy 11 wagi te są następujące:
![]()
; ![]()
.
Parametrami rozkładu takiego portfela są:
![]()
,
![]()
.
W tym przypadku zatem, dzięki krótkiej sprzedaży waloru B, można skonstruować portfel, którego oczekiwany zysk jest ujemny, zaś ryzyko wynosi zero.
3.4. Ryzyko portfela, gdy ![]()
Współczynnik korelacji między stopami zwrotu równy 0,5 oznacza występowanie ,,umiarkowanej'' dodatniej korelacji między stopami zwrotu. Współczynnik o tej (lub przybliżonej) wartości może być statystycznie istotny lub statystycznie nieistotny, co zależy od liczebności próby na podstawie której jest szacowany. Wariancja portfela jest w tej sytuacji równa:
![]()
.
Oznacza to, że uzyskaliśmy redukcję ryzyka, w stosunku do ![]()
.
W tablicy 12 pokazano wyliczone wartości oczekiwanych stóp zwrotu portfela oraz błędu standardowego portfela (ryzyka) w zależności od wag portfelowych (bez możliwości krótkiej sprzedaży). W omawianym przypadku występuje nieliniowa zależność między wartością oczekiwaną a odchyleniem standardowym portfela.
Tablica 12. Parametry rozkładu portfela, gdy ![]()
|
|
|
|
|
1,5 |
-0,5 |
1,0 |
42,25 |
6,50 |
1,2 |
-0,2 |
2,2 |
28,96 |
5,38 |
1,0 |
0,0 |
3,0 |
25,00 |
5,00 |
0,9 |
0,1 |
3,4 |
24,49 |
4,95 |
0,8 |
0,2 |
3,8 |
24,96 |
4,99 |
0,5 |
0,5 |
5,0 |
32,25 |
5,68 |
0,2 |
0,8 |
6,2 |
48,36 |
6,95 |
0,0 |
1,0 |
7,0 |
64,00 |
8,00 |
-0,2 |
1,2 |
7,8 |
83,56 |
9,14 |
-0,5 |
1,5 |
9,0 |
120,25 |
10,97 |
Źródło: opracowanie własne
Porównując obliczenia zawarte w tablicy 12 z tymi, które zawarto w tablicy 11 (dla ![]()
) zauważamy, że odchylenia standardowe portfela o takiej samej strukturze są tutaj nie większe. W wierszu oznaczonym (![]()
), znajdują się parametry portfela o najmniejszej wariancji. Widać zatem, że można skonstruować portfel składający się z dwóch walorów ryzykownych A i B (bez krótkiej sprzedaży), którego oczekiwany zysk jest dodatni i dla którego ryzyko ![]()
jest mniejsze od najmniejszego ryzyka składowej portfela ![]()
. Parametry rozkładu stopy zwrotu takiego portfela obliczono stosując omówione wyżej wzory. Oczekiwany zysk portfela o najmniejszej wariancji wynosi zatem:
![]()
,
natomiast wariancja stopy zwrotu portfela jest równa:
![]()
.
W konsekwencji odchylenie standardowe stopy zwrotu wyniesie:
![]()
.
Realizacje stopy zwrotu omawianego portfela odchylać się mogą od oczekiwanej stopy zwrotu równej ![]()
, przeciętnie rzecz biorąc in plus in minus o ![]()
. W pozostałych zacieniowanych wierszach tablicy 12 zamieszczono charakterystyki przykładowych portfeli składających się z waloru A i B, w których nie stosowano krótkiej sprzedaży.
Zakładając możliwość krótkiej sprzedaży waloru B lub A otrzymamy możliwość zwiększenia (zmniejszenia) wartości oczekiwanej portfela. Przykładowe portfele z krótką sprzedażą pokazane są w zacieniowanych wierszach tablicy 12. W dwóch pierwszych zacieniowanych wierszach tej tablicy zapisano wyniki obliczeń w sytuacji, w której inwestor zajmuje krótką pozycję w stosunku do waloru B, a uzyskaną w trakcie krótkiej sprzedaży kwotę przeznacza na dodatkową inwestycje w walor A. W dwóch ostatnich zacieniowanych wierszach jest odwrotnie. Z uwagi na nieliniową zależność między wartością oczekiwaną portfela a jego ryzykiem (błędem standardowym) nie jest już możliwe liniowe zmniejszanie ryzyka poprzez krótką sprzedaż.
3.5. Ryzyko portfela, gdy ![]()
Obecnie rozważana jest sytuacja, gdy stopy zwrotu nie są skorelowane. Oznacza to, że realizacje dwóch stóp zwrotu są względem siebie przypadkowe. Wariancja portfela jest w tej sytuacji równa:
![]()
.
Ryzyko portfela nie jest, tak jak poprzednio, ważoną sumą ryzyka akcji A oraz B. Ponownie zatem uzyskujemy redukcję ryzyka, w stosunku do ![]()
.
Tablica 13. Parametry rozkładu portfela, gdy ![]()
|
|
|
|
|
1,5 |
-0,5 |
1,0 |
72,25 |
8,50 |
1,2 |
-0,2 |
2,2 |
38,56 |
6,21 |
1,0 |
0,0 |
3,0 |
25,00 |
5,00 |
0,8 |
0,2 |
3,8 |
18,56 |
4,31 |
0,72 |
0,28 |
4,12 |
17,98 |
4,24 |
0,5 |
0,5 |
5,0 |
22,25 |
4,72 |
0,2 |
0,8 |
6,2 |
41,96 |
6,48 |
0,0 |
1,0 |
7,0 |
64,00 |
8,00 |
-0,2 |
1,2 |
7,8 |
93,16 |
9,65 |
-0,5 |
1,5 |
9,0 |
150,25 |
12,26 |
Źródło: opracowanie własne
W niezacieniowanych wierszach tablicy 13 zamieszczono charakterystyki rozkładu stóp zwrotu portfela w zależności od wag portfelowych bez możliwości krótkiej sprzedaży. W wierszu oznaczonym (![]()
) znajdują się parametry portfela o najmniejszej wariancji. Widać zatem, że można skonstruować portfel składający się z dwóch walorów ryzykownych A i B (bez krótkiej sprzedaży), którego ryzyko ![]()
jest wyraźnie mniejsze od najmniejszego ryzyka składowej portfela ![]()
. Dla lepszego zrozumienia zagadnienia, pokażemy sposób obliczenia charakterystyk portfela równomiernego, dla którego wagi są równe, tj. ![]()
, ![]()
. Wartością oczekiwanej stopy zwrotu będzie:
![]()
,
natomiast wariancja stopy zwrotu tego portfela:
![]()
.
Zauważmy, że w tym przypadku ryzyko kowariancyjne portfela jest równe zero, gdyż współczynnik korelacji stóp zwrotu jest zerowy. Odchylenie standardowe stopy zwrotu portfela wynosi:
![]()
,
co oznacza, że realizacje stopy zwrotu portfela odchylać się będą od oczekiwanej stopy zwrotu równej 5,0% przeciętnie rzecz biorąc, plus minus o 4,72%.
Jeśli dopuścimy możliwość krótkiej sprzedaży, podobnie jak poprzednio, otrzymamy portfele, których oczekiwane stopy zwrotu mogą być większe (mniejsze) od stóp zwrotu dla portfeli jednoelementowych. Przykładowe portfele zakładające krótką sprzedaż waloru A lub B prezentujemy w zacienionych wierszach tablicy 13.
3.6. Ryzyko portfela, gdy ![]()
Obecnie rozważana jest sytuacja, gdy stopy zwrotu są skorelowane ujemnie. Wariancja portfela jest w tej sytuacji równa:
![]()
.
W przypadku ujemnej korelacji stóp zwrotu walorów tworzących portfel, ryzyko kowarianacyjne ma znak minus. Uzyskujemy zatem znaczącą redukcję ryzyka, w stosunku do ![]()
.
W niezacieniowanych wierszach tablicy 14 pokazano wyliczone wartości oczekiwanych stóp zwrotu portfela oraz błędu standardowego portfela (ryzyka) w zależności od wag portfelowych (bez możliwości krótkiej sprzedaży).
Tablica 14. Parametry rozkładu portfela, gdy ![]()
|
|
|
|
|
1,5 |
-0,5 |
1,0 |
102,25 |
10,11 |
1,2 |
-0,2 |
2,2 |
48,16 |
6,94 |
1,0 |
0,0 |
3,0 |
25,00 |
5,00 |
0,8 |
0,2 |
3,8 |
12,16 |
3,49 |
0,65 |
0,35 |
4,40 |
9,30 |
3,05 |
0,5 |
0,5 |
5,0 |
12,25 |
3,50 |
0,2 |
0,8 |
6,2 |
35,56 |
5,96 |
0,0 |
1,0 |
7,0 |
64,00 |
8,00 |
-0,2 |
1,2 |
7,8 |
102,76 |
10,14 |
-0,5 |
1,5 |
9,0 |
180,25 |
13,43 |
Źródło: opracowanie własne
W wierszu oznaczonym (![]()
), znajdują się parametry portfela o najmniejszej wariancji. Widać zatem, że można skonstruować portfel składający się z dwóch walorów ryzykownych A i B (bez krótkiej sprzedaży), którego ryzyko ![]()
, na skutek ujemnego znaku ryzyka kowariancyjnego, jest wyraźnie mniejsze od najmniejszego ryzyka składowej portfela ![]()
.
Jeśli dopuścimy możliwość krótkiej sprzedaży, podobnie jak poprzednio, otrzymamy portfele, których oczekiwane stopy zwrotu mogą być większe (mniejsze) od stóp zwrotu dla portfeli jednoelementowych. Przykładowe portfele zakładające krótką sprzedaż waloru A lub B prezentujemy w zacienionych wierszach tablicy 14. Pokażemy obecnie w jaki sposób wyznaczono charakterystyki portfela z krótką sprzedażą waloru B, zamieszczone w pierwszym wierszu tablicy 14. Ponieważ wagi portfelowe wynoszą ![]()
oraz ![]()
, zatem oczekiwany zysk takiego portfela wyniesie:
![]()
,
natomiast wariancja stopy zwrotu:
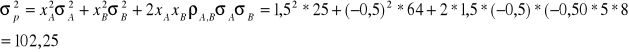
W konsekwencji ryzyko mierzone odchylenie standardowym będzie równe:
![]()
.
Zatem realizacje stopy zwrotu takiego portfela odchylać się mogą od oczekiwanej stopy zwrotu równej 1,0% przeciętnie rzecz biorąc plus, minus o 10,11%. Widzimy zatem, oczekiwany zysk portfela jest niższy od najmniejszego zysku składowych portfela, natomiast ryzyko portfela w którym wykorzystano krótką sprzedaż jednego z walorów jest znacząco większe od największego ryzyka składowych portfela. Jest tak dlatego, że opisany wyżej portfel zakłada krótką sprzedaż ,,lepszego'' waloru B i dodatkową inwestycję w ,,gorszy'' walor A. W dwóch ostatnich wierszach tablicy 15 przedstawiono charakterystyki portfeli w których wykorzystano krótką sprzedaż waloru ,,gorszego'' A i dodatkową inwestycję w walor B. Skutkuje to możliwością otrzymania wyższego niż 7% oczekiwanego zysku portfela ale też wyższym niż 8% ryzykiem portfela.
3.7. Ryzyko portfela, gdy ![]()
Ujemna korelacja pomiędzy stopami zwrotu dwóch walorów oznacza, że przeciętnie rzecz biorąc realizacje tych stóp zwrotu są przeciwne. Wzrostowi stopy zwrotu jednego waloru odpowiada spadek stopy zwrotu drugiego i odwrotnie. W szczególności funkcyjna korelacja ujemna (![]()
) pozwala zredukować ryzyko portfela do zera. Wariancja portfela jest w tej sytuacji równa:
![]()
.
natomiast ryzyko portfela mierzone odchyleniem standardowym stopy zwrotu jest równe:
![]()
jeżeli ![]()
lub
![]()
jeżeli ![]()
.
W rozpatrywanym obecnie przypadku możemy skonstruować portfel bez ryzyka tj. ![]()
. Możemy obliczyć wagi portfelowe dla których spełnione jest zapisane wyżej równanie. Otrzymamy:
![]()
![]()
![]()
i ![]()
lub równoważnie
![]()
![]()
![]()
i ![]()
.
W rozpatrywanym przez nas przykładzie wagi zapewniające otrzymanie portfela bez ryzyka wynoszą:
![]()
; ![]()
.
Oczekiwany zysk oraz ryzyko takiego portfela wynoszą zatem:
![]()
,
![]()
,
co oznacza, że konstruując portfel z dwóch walorów ryzykownych A i B, o strukturze określonej przez wagi ![]()
oraz ![]()
, możemy oczekiwać zysku równego 4,54% bez ponoszenia ryzyka.
Zauważmy, że efekt znoszenia się ryzyka występuje dlatego, że waga ![]()
jest wprost proporcjonalna do ryzyka waloru B, natomiast waga ![]()
jest proporcjonalna do ryzyka waloru A. Ponieważ skorelowanie stóp zwrotu jest ,,przeciwne'', w tym sensie, że współczynnik korelacji równa się -1, zatem nawet intuicyjnie zrozumiałe jest, że ryzyko portfela wyniesie zero.
Z uwagi na to, że odchylenia standardowe są zawsze nieujemne, wynika stąd, iż dla dokładnego ujemnego skorelowania stóp zwrotu, istnieje zawsze rozwiązanie zapewniające zero ryzyka, przy wagach nieujemnych. Zatem ryzyko może tutaj być wyeliminowane całkowicie bez występowania krótkiej sprzedaży.
Zależność między ryzykiem a oczekiwaną stopą zwrotu daje się opisać za pomocą dwóch prostych przecinających się w punkcie, dla którego ryzyko jest zerowe. Rozwiązując układ równań:
![]()
![]()
dla ![]()
oraz
![]()
![]()
dla ![]()
, otrzymujemy odpowiednio równania dwóch prostych:
![]()
oraz
![]()
.
Wykorzystując dane z rozpatrywanego przykładu otrzymamy:
![]()
oraz
![]()
.
Proste te przecinają się w punkcie ![]()
; ![]()
. W tym punkcie znajduje się portfel o najmniejszym ryzyku równym zeru. Pokazaliśmy powyżej, że wagi tego portfela wynoszą: ![]()
, ![]()
.
W tablicy 15 zamieszczono wartości oczekiwane oraz odchylenia standardowe stóp zwrotu przykładowych portfeli, w przypadku gdy występuje ścisła ujemna korelacja pomiędzy stopami zwrotu składowych portfela. Ponownie nastąpiła redukcja ryzyka w porównaniu do ![]()
. W niezacieniowanych wierszach tablicy 15 pokazano przykładowe portfele bez krótkiej sprzedaży, przy czym jednym z nich jest portfel o ryzyku zerowym (w wierszu oznaczonym ![]()
).
Jeśli dopuścimy możliwość krótkiej sprzedaży, podobnie jak poprzednio otrzymamy portfele, których oczekiwana stopa zwrotu może być większa (mniejsza) od stopy zwrotu dla portfeli jednoelementowych. Przykładowe portfele zakładające krótką sprzedaż waloru A lub B prezentujemy w zacieniowanych wierszach tablicy 15.
Tablica 15. Parametry rozkładu portfela, gdy ![]()
|
|
|
|
|
1,5 |
-0,5 |
1,0 |
132,25 |
11,50 |
1,2 |
-0,2 |
2,2 |
57,76 |
7,60 |
1,0 |
0,0 |
3,0 |
25,00 |
5,00 |
0,8 |
0,2 |
3,8 |
5,76 |
2,40 |
0,62 |
0,38 |
4,52 |
0,00 |
0,00 |
0,5 |
0,5 |
5,0 |
2,25 |
1,50 |
0,2 |
0,8 |
6,2 |
29,16 |
5,40 |
0,0 |
1,0 |
7,0 |
64,00 |
8,00 |
-0,2 |
1,2 |
7,8 |
112,36 |
10,60 |
-0,5 |
1,5 |
9,0 |
210,25 |
14,50 |
Źródło: opracowanie własne
Jeśli dopuścimy możliwość krótkiej sprzedaży, podobnie jak poprzednio otrzymamy portfele, których oczekiwana stopa zwrotu może być większa (mniejsza) od stopy zwrotu dla portfeli jednoelementowych. Przykładowe portfele zakładające krótką sprzedaż waloru A lub B prezentujemy w zacieniowanych wierszach tablicy 15.
3.8. Krzywa minimalnego ryzyka
W tablicy 16 i 17 zestawiono, dla porównania, wyniki do tej pory przeprowadzonych analiz.
Tablica 16. Parametry rozkładu portfela w zależności od skorelowania stóp zwrotu
|
|
|
1,0 |
|
|
0,5 |
|
|
0,0 |
|
|
-0,5 |
|
|
-1,0 |
|
|
Źródło: opracowanie własne
Na podstawie tablicy 16 wnioskujemy, że oczekiwany zysk portfela ![]()
, będący kombinacją liniową oczekiwanych zysków składowych portfela, nie zależy od siły i kierunku skorelowania stóp zwrotu walorów ten portfel tworzących. Odmiennie jest w przypadku ryzyka portfelowego. Tutaj istotne znaczenie ma skorelowanie stóp zwrotu walorów wchodzących w skład portfela, z uwagi na to, że ryzyko kowariancyjne zależy od współczynnika korelacji. W miarę zmniejszania się tego współczynnika (przy innych parametrach niezmienionych), całkowite ryzyko portfela maleje.
W tablicy 17 natomiast zestawione są najważniejsze wyniki obliczeń dotyczące przykładowego portfela składającego się z walorów ryzykownych A i B. Wiersze niezaciemnione tej tablicy ukazują parametry portfeli utworzonych bez krótkiej sprzedaży, podczas gdy wiersze zaciemnione dotyczą portfeli, w których jeden z walorów jest krótko sprzedany. Wszystkie te portfele leżą na krzywych zamieszczonych na rysunku 11. W wierszach oznaczonych (![]()
) pokazano parametry portfeli o najmniejszym ryzyku (MVP) dla danej wartości współczynnika korelacji.
Tablica 17. Parametry rozkładu portfela w zależności od skorelowania stóp zwrotu walorów tworzących portfel
|
|
|
|
||||
|
|
|
|
|
|
|
|
2,67 |
-1,67 |
-3,67 |
0,00 |
|
|
|
|
1,5 |
-0,5 |
1,00 |
3,50 |
6,50 |
8,50 |
10,11 |
1,50 |
1,2 |
-0,2 |
2,20 |
4,40 |
5,38 |
6,21 |
6,94 |
7,60 |
1,0 |
0,0 |
3,00 |
5,00 |
5,00 |
5,00 |
5,00 |
5,00 |
0,9 |
0,1 |
3,40 |
|
4,95 |
|
|
|
0,8 |
0,2 |
3,80 |
5,60 |
4,99 |
4,31 |
3,49 |
2,40 |
0,72 |
0,28 |
4,12 |
|
|
4,24 |
|
|
0,65 |
0,35 |
4,40 |
|
|
|
3,05 |
|
0,62 |
0,38 |
4,54 |
|
|
|
|
0,00 |
0,5 |
0,5 |
5,00 |
6,50 |
5,68 |
4,72 |
3,50 |
1,50 |
0,2 |
0,8 |
6,20 |
7,40 |
6,95 |
6,48 |
5,96 |
5,40 |
0,0 |
1,0 |
7,00 |
8,00 |
8,00 |
8,00 |
8,00 |
8,00 |
-0,2 |
1,2 |
7,80 |
8,60 |
9,14 |
9,65 |
10,14 |
10,60 |
-0,5 |
1,5 |
9,00 |
9,50 |
10,97 |
12,26 |
13,43 |
14,50 |
Źródło: opracowanie własne
W dwóch przypadkach możliwe jest stworzenie portfela, składającego się z walorów ryzykownych, który sam jest pozbawiony ryzyka. W sytuacji pierwszej, gdy występuje ścisła korelacja ujemna, ryzyko może być całkowicie wyeliminowane, poprzez wybór odpowiedniej struktury portfela (wagi wprost proporcjonalne do ryzyka przeciwnego waloru). Portfel taki nie wykorzystuje krótkiej sprzedaży. W sytuacji drugiej, gdy występuje ścisła korelacja dodatnia stóp zwrotu walorów tworzących portfel, ryzyko może być całkowicie wyeliminowane poprzez stworzenie portfela wykorzystującego krótką sprzedaż waloru o wyższym ryzyku i dodatkową inwestycje w walor o niższym ryzyku. Prawdziwy jest zatem wniosek, że ryzyko portfela zależy nie tylko od doboru odpowiednich wag portfelowych (od struktury portfela), ale również od siły i kierunku skorelowania walorów uwzględnionych w portfelu. Warto też zauważyć, że spośród wielu różnych portfeli można wybrać taki, który dla danego współczynnika korelacji stóp zwrotu ![]()
charakteryzuje się najmniejszym ryzykiem. Rysunek 11, na którym wykreślono zależności między oczekiwaną stopą zwrotu portfela a jego ryzykiem, na podstawie danych zawartych w tablicy 17, potwierdza sformułowane powyżej wnioski. Sposób wyboru takiego portfela omówimy poniżej.
Zapiszmy raz jeszcze wzór na wariancję portfela, wykorzystując równość ![]()
:
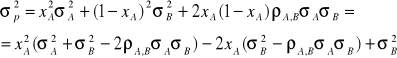
Obliczając pierwszą pochodną względem ![]()
otrzymamy:
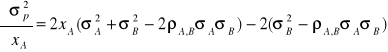
.
Przyrównując pierwszą pochodną do zera oraz przekształcając, otrzymujemy wzór na wagę ![]()
, przy której ![]()
osiąga wartość minimalną:
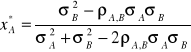
oraz
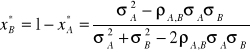
.
Jest tak dlatego, gdyż druga pochodna wariancji jest nieujemna:
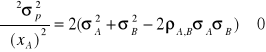
.
Zauważmy, że istnieją przypadki, w których dwuskładnikowy portfel o globalnie najmniejszej wariancji musi wykorzystywać krótką sprzedaż jednego z walorów. Jest tak wtedy, gdy np. ![]()
. Rozważmy następujący przykład. Niech portfel składa się z dwóch akcji, których rozkłady stóp zwrotu opisywane są przez następujące parametry: ![]()
; ![]()
; ![]()
; ![]()
; ![]()
. W takim przypadku optymalne wagi portfelowe wynoszą: ![]()
; ![]()
. Portfel ten ma następujące parametry:
![]()
; ![]()
; ![]()
.
Analizując portfele o najmniejszej wariancji, zamieszczone w tablicy 17, widzimy że minimalne ryzyko wzrasta, gdy rośnie skorelowanie walorów tworzących portfel.
Na rysunku 11 oznaczono literami (a), (b), (c), (d), (e) zbiory wszystkich możliwych portfeli utworzonych z walorów A i B, przy zachowaniu warunku, że suma wag portfelowych jest równa jedności. Literą (a) oznaczono prostą do której należy odcinek AB. Na odcinku AB leżą wszystkie portfele utworzone z A i B (bez wykorzystania krótkiej sprzedaży), przy założeniu, że współczynnik korelacji pomiędzy stopami zwrotu walorów A i B jest równy jedności. Na półprostej od punktu B w górę leżą portfele utworzone z krótko sprzedanego waloru A oraz z waloru B. Na odcinku AE, leżą portfele utworzone z waloru B oraz krótko sprzedanego waloru A. W szczególności portfel leżący w punkcie E jest pozbawiony ryzyka.
Krzywa oznaczona (b) jest obrazem graficznym wszystkich portfeli utworzonych z walorów A i B, przy założeniu, że współczynnik korelacji pomiędzy stopami zwrotu tych walorów jest równy ![]()
. Krzywa oznaczona (c) jest obrazem graficznym wszystkich portfeli utworzonych z walorów A i B, przy założeniu, że współczynnik korelacji pomiędzy stopami zwrotu tych walorów jest równy ![]()
. Krzywa oznaczona (d) jest obrazem graficznym wszystkich portfeli utworzonych z walorów A i B, przy założeniu, że współczynnik korelacji pomiędzy stopami zwrotu tych walorów jest równy ![]()
.
Portfele leżące na segmentach tych krzywych pomiędzy punktami A i B są skonstruowane bez wykorzystania krótkiej sprzedaży. Portfele leżące na ramionach krzywych na prawo od punktu B są skonstruowane z wykorzystaniem krótkiej sprzedaży waloru A, natomiast na prawo od punktu A skonstruowane są z wykorzystaniem krótkiej sprzedaży waloru B.
Dwie półproste, przecinające się w punkcie ![]()
, są obrazem graficznym portfeli utworzonych z A i B, przy założeniu, że współczynnik korelacji pomiędzy stopami zwrotu tych walorów jest równy ![]()
. W punkcie ![]()
leży portfel pozbawiony ryzyka. Jednym z elementów każdej krzywej zamieszczonej na rysunku 11 jest portfel o najmniejszej wariancji spośród wszystkich możliwych portfeli. Dla większej przejrzystości zobrazujemy to na rysunku 12.
Rysunek 12 pokazuje krzywą ACDB, która jest obrazem graficznym portfeli utworzonych z walorów A i B (dla pewnego współczynnika korelacji ![]()
). Każdy punkt tej krzywej obrazuje portfel minimalnego ryzyka dla założonego poziomu oczekiwanego zysku. Oznacza to, że dla założonego poziomu oczekiwanego zysku nie można utworzyć portfela o mniejszym ryzyku, przy założeniu, że suma wag portfelowych ![]()
, niż takie jakimi charakteryzują się portfele na omawianej krzywej. Portfel MVP, jest portfelem o globalnie najmniejszym ryzyku, spośród wszystkich portfeli (niezależnie od poziomu oczekiwanego zysku). W szczególności (dla ![]()
) portfel ten leży na osi odciętych - tzn. jest portfelem pozbawionym ryzyka. Portfel MVP rozdziela krzywą minimalnego ryzyka na dwa segmenty:
- zbiór portfeli efektywnych - krzywa MVP-D-B (łącznie z portfelem MVP),
- zbiór portfeli nieefektywnych - krzywa MVP-C-A (bez portfela MVP).
Różnicę pomiędzy wymienionymi wyżej rodzajami portfeli pokazuje przykład portfela C i D. Zauważmy, że zachodzi:
![]()
oraz ![]()
.
Zatem portfel D jest efektywny w stosunku do C w tym sensie, że umożliwia otrzymanie wyższego oczekiwanego zysku przy zadanym poziomie ryzyka. Taką własnością charakteryzują się wszystkie portfele leżące na górnym segmencie krzywej minimalnego ryzyka (krzywej efektywnej). Mają one swoje odpowiedniki - portfele leżące na dolnym segmencie krzywej minimalnego ryzyka (krzywej nieefektywnej).
Możemy obecnie podać definicję portfela efektywnego i nie nieefektywnego. Portfelem efektywnym nazywać będziemy taki portfel, który posiada dwie własności:
dla zadanego poziomu oczekiwanego zysku, charakteryzuje się najmniejszym ryzykiem i jednocześnie dla zadanego poziomu ryzyka charakteryzuje się największym możliwym do zrealizowania oczekiwanym zyskiem.
Portfelem nieefektywnym nazywać będziemy taki portfel, który spełnia tylko pierwszą własność, tj. dla zadanego poziomu oczekiwanego zysku, charakteryzuje się najmniejszym ryzykiem, natomiast dla zadanego poziomu ryzyka można znaleźć dla niego portfel oferujący wyższy oczekiwany zysk (portfel efektywny).
Rysunek 11. Dwuelementowe portfele utworzone z walorów A i B, przy różnych
wartościach współczynnika korelacji
![]()
8 a b c d e
7
B
6
![]()
5 ![]()
![]()
![]()
![]()
![]()
4
![]()
3 A e
2 a b c d
1
1 2 3 4 5 6 7 8 ![]()
E
Źródło: opracowanie własne
Wprowadzając rozróżnienie pomiędzy portfelami bez oraz z krótką sprzedażą wyróżnimy następujące segmenty krzywej minimalnego ryzyka na rysunku 12:
krzywa MVP-B (łącznie z portfelem MVP) - krzywa portfeli efektywnych, bez krótkiej sprzedaży jakiegokolwiek waloru,
krzywa od punktu B w górę (bez portfela B) - krzywa portfeli efektywnych, z krótką sprzedażą waloru A i dodatkową inwestycją w walor B,
krzywa MVP-A (bez portfela MVP) - krzywa portfeli nieefektywnych, bez krótkiej sprzedaży jakiegokolwiek waloru,
krzywa od punktu A w dół (bez portfela A) - krzywa portfeli nieefektywnych z krótką sprzedażą waloru B i dodatkową inwestycją w walor A.
Rysunek 12. Krzywa możliwych portfeli i jej segmenty
![]()
8
7
B
6
D
5
MVP
4
C
3 A
1
0 1 2 3 4 5 6 7 8 ![]()
Źródło: opracowanie własne
Skoro na płaszczyźnie ryzyko-dochód istnieje zbiór portfeli efektywnych, powstaje pytanie który z nich wybierze inwestor kierujący się zasadą maksymalizacji oczekiwanej użyteczności bogactwa (stopy zwrotu)? Odwołując się do wiedzy zawartej w wykładzie dotyczącym podstaw wyboru w warunkach ryzyka możemy przywołać pojęcie funkcji jednakowej użyteczności, określonej także na płaszczyźnie ryzyko dochód. Dla inwestora niechętnego ryzyku, kształt tej funkcji zależeć będzie od współczynnika niechęci wobec ryzyka. Pokazuje to rysunek 13.
Inwestor niechętny wobec ryzyka i charakteryzujący się krzywą obojętności jak na rysunku 13 wybierze portfel W, leżący na krzywej portfeli efektywnych, gdyż zapewnia on osiągnięcie najwyższej, możliwej oczekiwanej użyteczności na poziomie równym ![]()
. Inni inwestorzy, również niechętni wobec ryzyka, ale charakteryzujący się innym współczynnikiem niechęci wobec ryzyka, będą wybierać inne portfele znajdujące się na krzywej portfeli efektywnych.
Rysunek 13. Wybór inwestora niechętnego wobec ryzyka
![]()
![]()
![]()
8 ![]()
7
B
6
W
5
MVP
4
3 A
1
0 1 2 3 4 5 6 7 8 ![]()
Źródło: opracowanie własne
4. Portfel zawierający walor pozbawiony ryzyka
4.1. Walor pozbawiony ryzyka
Walory dostępne na rynku można podzielić wedle stopnia ryzyka z nimi związanego na ryzykowne (akcje, prawa poboru, opcje) oraz walory pewne (obligacje rządowe). W warunkach równowagi walor pewny przynosi zwykle mniejszy zysk niż papier ryzykowny.
W trakcie poprzedniego wykładu pokazano, że przez dobór odpowiednich wag możemy wyznaczyć portfele charakteryzujące się różnymi oczekiwanymi stopami zwrotu oraz różnym ryzykiem. Portfele takie nazywamy portfelami ryzykownymi. Obecnie przejdziemy do omówienia portfeli zawierających, oprócz walorów ryzykownych, walor pozbawiony ryzyka. Wprowadźmy oznaczenie ![]()
dla stopy zwrotu (zysku) waloru pozbawionego ryzyka (risk free rate). Z definicji waloru ,,pewnego'' (przynoszącego pewny dochód) wynika, że:
![]()
; ![]()
.
Zatem dochód pewny jest osiągany ,,z ryzykiem zerowym''. Oznaczmy literką C dowolny walor ryzykowny. Niech ![]()
, ![]()
, ![]()
, oznaczają kolejno: stopę zysku waloru C, jej wartość oczekiwaną oraz odchylenie standardowe. Ponieważ papier ryzykowny przynosi, jak powiedzieliśmy, dochód nie mniejszy niż papier pewny, zatem
![]()
.
Oznaczmy ponadto:
![]()
wagę portfelową dla waloru pewnego, oznaczającą część funduszu przeznaczonego na jego zakup ![]()
. Waga waloru ryzykownego będzie w tym przypadku
![]()
.
Wagi te sumować się będą do jedności ![]()
, bez względu na to, czy występuje możliwość pożyczania dodatkowych pieniędzy po stopie wolnej od ryzyka, czy też nie. Obie sytuacje zostaną w dalszej części wykładu oddzielnie omówione.
4.2. Parametry rozkładu portfela
Załóżmy, że inwestor chce skonstruować portfel inwestycyjny składający się z waloru ryzykownego oraz waloru przynoszącego zysk pewny. Stopą zwrotu portfela o takiej strukturze jest:
![]()
natomiast wartością oczekiwaną
![]()
.
Wariancją stopy zwrotu tak skonstruowanego portfela jest natomiast:
![]()
.
Zatem ryzyko portfela zawierającego walor pewny wynosi:
![]()
.
Ryzyko to jest proporcjonalne do wagi waloru ryzykownego w portfelu ![]()
. W sytuacji, w której:
- ![]()
- cały fundusz jest inwestowany w walory ryzykowne, wtedy ![]()
- nie ma redukcji ryzyka,
- ![]()
- cały fundusz inwestowany w obligacje rządowe, wtedy ![]()
- ryzyko jest zerowe.
Zwiększając udział papierów pozbawionych ryzyka w portfelu zmniejszamy ryzyko portfela. Wniosek jest oczywisty. Objaśnia to dokładnie rysunek 14. Odcinek FC definiuje dwuskładnikowe kombinacje ryzykownego waloru C oraz waloru pewnego F. Punkty ![]()
, ![]()
, ![]()
na tym odcinku oznaczają portfele o różnej strukturze. Pierwszy z nich oznacza portfel o większym udziale papieru ryzykownego, drugi oznacza portfel równomierny, natomiast trzeci o większym udziale papieru pozbawionego ryzyka.
Przesuwając się od punktu C w kierunku punktu F otrzymujemy portfele zawierające coraz większy udział papierów pewnych. Portfele takie mają coraz mniejsze ryzyko i coraz mniejszą wartość oczekiwaną. Posuwając się od punktu F w górę po odcinku FC otrzymujemy portfele o coraz mniejszym udziale papierów pewnych. Zatem są one coraz bardziej ryzykowne lecz przynoszą większy oczekiwany zysk. Przykład prezentuje obliczenia, które stały się podstawą wykonania rysunku 14.
Przyjmijmy następujące założenia:
- oczekujemy, że ryzykowny walor C przyniesie ![]()
zysku w ciągu okresu, z ryzykiem ![]()
,
- walor pewny daje ![]()
zysku w ciągu tego samego okresu bez ryzyka,
- rozpatrujemy trzy portfele o różnej strukturze:
- dla punktu ![]()
- ![]()
, ![]()
,
- dla punktu ![]()
- ![]()
, ![]()
,
- dla punktu ![]()
- ![]()
, ![]()
.
Współrzędnymi punktu C są ![]()
, zaś punktu F - ![]()
. Korzystając ze wcześniej podanych wzorów na wartość oczekiwaną i ryzyko portfela otrzymujemy:
![]()
; ![]()
dla punktu ![]()
, którego współrzędnymi są zatem ![]()
,
![]()
; ![]()
dla punktu ![]()
o współrzędnych ![]()
oraz
![]()
; ![]()
dla punktu ![]()
o współrzędnych ![]()
.
Współczynnikiem kierunkowym prostej przechodzącej przez punkty FC jest:
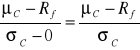
.
Określa on dodatkową wielkość oczekiwanego zysku, jaką otrzymamy zwiększając ryzyko portfela o 1%.
Wykorzystując dane z przykładu otrzymujemy:
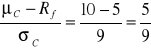
,
co oznacza, że jednoprocentowemu przyrostowi ryzyka portfela odpowiada przyrost oczekiwanego zysku o (5/9)%. Przykładowo, jeśli chcemy utrzymywać portfel charakteryzujący się ryzykiem ![]()
, wtedy powinien on przynosić ![]()
ponad stopę pewną, równą ![]()
. Zatem łączną stopą zysku jest ![]()
. Ponieważ chcemy, by ![]()
, zatem waga portfelowa może być obliczona ze wzoru :
![]()
czyli z równania ![]()
. Tak więc ![]()
natomiast ![]()
. Rzeczywiście portfel o takiej strukturze charakteryzuje się oczekiwanym zyskiem równym:
![]()
.
Rysunek 14. Portfele składające się z waloru ryzykownego C i pewnego F
![]()
11 P'''
C
9
P
P'
7
P''
5 F
3
1
1 2 3 4 5 6 7 8 9 10 11 12 ![]()
Źródło: opracowanie własne
4.3. Możliwość pożyczania
Na odcinku FC leżą tylko takie portfele, dla których ![]()
. Zatem inwestor wykorzystuje tylko kwotę F posiadaną przez siebie. Przez fakt zakupu obligacji - inwestor pożycza rządowi ![]()
swoich pieniędzy oczekując pewnego zysku w wysokości ![]()
. Na rysunku 14 pokazujemy inną jeszcze sytuację, obrazowaną przez punkty znajdujące się na prostej od punktu C w górę. Na tej półprostej znajdują się kombinacje ryzykowne, które powstają, gdy inwestor pożycza dodatkowo pewną sumę pieniędzy, po stopie równej ![]()
i przeznacza ją na dodatkową inwestycję w walor C.
Niech ![]()
oznacza kwotę pożyczoną na ![]()
% i przeznaczoną na dodatkową inwestycję w walor C. Wtedy:
![]()
; ![]()
.
Tak więc waga odpowiadająca walorowi pewnemu jest ujemna. Walor pewny nie jest kupowany, natomiast inwestor dodatkowo pożycza pieniądze by przeznaczyć je na dodatkową inwestycję w walor C.
Inwestor posiada kwotę ![]()
złotych i inwestuje ją w walor C, charakteryzujący się oczekiwanym zyskiem ![]()
i ryzykiem ![]()
. Pożycza kwotę ![]()
złotych na ![]()
i dodatkowo zakupuje walor C. Zatem wagi portfelowe są następujące:
![]()
; ![]()
.
Portfel ten, na rysunku 14 oznaczony ![]()
charakteryzuje się następującymi parametrami:
![]()
![]()
.
Współrzędnymi punktu ![]()
są więc ![]()
. Warto przy tej okazji podać dodatkowe wyjaśnienie. Inwestor zainwestował w walor C kwotę 1200 złotych, uzyskując 10% stopę zwrotu, a więc 1200x 0,1=120 złotych zysku. Z drugiej strony pożyczył 200 złotych na 5%, zatem musi oddać 200x 0,05=10 złotych. Zatem zysk netto z całej operacji jest 120-10=110 złotych, czyli stopa zysku wynosi (110/1000)x 100=11,0%.
Rysunek 15. Granica efektywna dla portfeli zawierających walor pewny
![]()
11
C
9 L M
K
7 N
5
F
3
1
1 2 3 4 5 6 7 8 9 10 11 12 ![]()
Źródło: opracowanie własne
Rysunek 15 pokazuje kombinację waloru pewnego z pojedynczym walorem ryzykownym C. Tymczasem inwestor ma możliwości wyboru między różnymi walorami ryzykownymi i łączenia ich z walorami pewnymi. W szczególności może łączyć portfele znajdujące się na granicy efektywnej. Na rysunku 15 przedstawiamy linię portfeli efektywnych oraz walor pewny (w punkcie F). Odcinki FN, FM reprezentują kombinacje waloru pewnego z różnymi portfelami efektywnymi, zawsze dla przypadku ![]()
. Zauważmy, że odcinki te definiują portfele ,,nie gorsze'' od tych, które znajdują się na krzywej efektywnej. Ponieważ portfele takie zapewniają ten sam zysk przy mniejszym ryzyku lub większy zysk oczekiwany, przy mniejszym ryzyku. Tworzą więc one nowe granice efektywne. Omówimy to na przykładzie portfela charakteryzującego się minimalną wariancją, na rysunku 15 oznaczono ten portfel N. Portfel K o współrzędnych ![]()
, ![]()
jest lepszy od portfela N, gdyż ma mniejsze ryzyko. Portfel L o współrzędnych ![]()
, ![]()
jest lepszy od portfela N, gdyż oferuje większy oczekiwany zysk.
Odcinek FM leżący na stycznej do krzywej portfeli efektywnych definiuje najlepsze kombinacje ryzykownych portfeli efektywnych z papierami pewnymi. Leżą tam bowiem portfele dające największe spodziewane dochody, przy danym poziomie ryzyka. Styczna ta ma więc największy współczynnik kierunkowy spośród wszystkich możliwych prostych przechodzących przez punkt F i dowolny punkt na krzywej portfeli efektywnych . Zatem jeśli na rynku występuje walor pozbawiony ryzyka, to granicą efektywną jest odcinek FM, jeśli inwestor nie pożycza na rynku kapitałowym środków pieniężnych po stopie wolnej od ryzyka lub półprostą FM, jeśli inwestor ma możliwości pożyczania środków pieniężnych po stopie wolnej od ryzyka.
4.4. Portfel rynkowy i linia rynku kapitałowego
Na odcinku FM leżą kombinacje, dla których ![]()
, zatem inwestor nie pożycza dodatkowych pieniędzy na rynku finansowym. Na prawo od punktu M znajdują się natomiast portfele, w których wykorzystana jest procedura pożyczania pieniędzy na procent równy ![]()
oraz przeznaczania tej pożyczki na dodatkowe inwestycje w portfel ryzykowny M. W punkcie M zatem ![]()
zaś ![]()
, czyli cały fundusz jest inwestowany w walory ryzykowne, leżące na linii rozwiązań efektywnych.
Portfel ryzykowny M nazywa się portfelem rynkowym, tj. takim, który daje najlepsze kombinacje z walorami pewnymi. Portfel rynkowy zawiera wszystkie walory mogące być przedmiotem handlu na rynku, w proporcji adekwatnej do udziału kapitalizacji każdego waloru w łącznej kapitalizacji rynku. Portfel rynkowy jest zatem reprezentantem rynku. Portfel taki, z uwagi na występowanie w nim wszystkich walorów, jest doskonale zdywersyfikowany, tzn. ryzyko portfela jest rozproszone pomiędzy dużą liczbę walorów. Prosta przechodząca przez punkty FM nazywa się linią rynku kapitałowego (capital market line).
Ponieważ portfel rynkowy M charakteryzują parametry: ![]()
, ![]()
, ![]()
, a więc stopa zwrotu, oczekiwana stopa zwrotu i ryzyko, papier pewny natomiast - ![]()
, ![]()
, zatem stopą zwrotu dowolnego portfela na prostej FM jest:
![]()
.
Wartością oczekiwaną stopy zwrotu takiego portfela jest:
![]()
.
natomiast jego ryzykiem:
![]()
.
Ryzyko to zależy od udziału papierów ryzykownych w portfelu oraz od ryzyka związanego z utrzymywaniem portfela rynkowego.
Równanie rynku kapitałowego znajdziemy rozwiązując układ równań:
![]()
,
![]()
.
Wyznaczając ![]()
z drugiego równania oraz wstawiając do równania pierwszego otrzymamy:
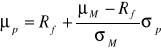
.
Współczynnik kierunkowy linii rynku kapitałowego:
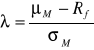
obrazuje relację pomiędzy ryzykiem a oczekiwanym zyskiem portfela rynkowego. Pokazuje on jaka jest nadwyżka oczekiwanej wartości portfela rynkowego nad stopę wolną od ryzyka, przypadająca na jednostkę ryzyka tego portfela. Współczynnik ![]()
nazywać będziemy rynkową ceną ryzyka. Tak więc oczekiwany zysk z efektywnej inwestycji jest równy zyskowi pewnemu ![]()
powiększonemu o premię z tytułu ponoszenia ryzyka rynkowego ![]()
. W konsekwencji linię rynku zapiszemy w postaci:
![]()
.
Załóżmy, że ![]()
, ![]()
, natomiast ![]()
. Wtedy linia rynku będzie miała postać:
![]()
.
Tak więc każdemu przyrostowi ryzyka o 1 procent odpowiada przyrost oczekiwanego zysku o 0,53% ponad stopę wolną od ryzyka.
Rysunek 16. Granica efektywna, gdy ![]()
![]()
11
X
Y
9 M
B
7
5 F
3
1
1 2 3 4 5 6 7 8 9 10 11 12 ![]()
Źródło: opracowanie własne
Rozważmy obecnie sytuację, w której stopa zysku z inwestycji w papiery rządowe (pewne) ![]()
nie jest równa stopie, po której inwestor pożycza środki pieniężne na rynku. Tę stopę procentową oznaczmy ![]()
. W ogólności zakładać będziemy, że: ![]()
.
Rysunek 16 pokazuje tę nową sytuację. Krzywa rozwiązań efektywnych nie jest już półprostą, lecz krzywą FMYX. W tej nowej granicy efektywnej odcinek FM zawiera portfele będące kombinacją portfela rynkowego M i papieru pewnego, krzywa MY zawiera kombinacje tylko papierów ryzykownych, natomiast półprosta YX portfele ryzykowne z wykorzystaniem dodatkowych pożyczonych funduszy.
Włączenie do portfela papieru wolnego od ryzyka przynosi zmniejszenie jego ryzyka. Optymalną kombinacją portfela ryzykownego i wolnego od ryzyka jest portfel rynkowy, którego parametry określają linię rynku kapitałowego. Współczynnik kierunkowy tej linii określa rynkową cenę ryzyka. Jest to premia, którą uzyskuje inwestor, w postaci nadwyżki nad stopę wolną od ryzyka, gdy zwiększa swoje ryzyko o jednostkę.
5. Dywersyfikacja portfela
5.1. Portfel trzech akcji
Rozważmy trzy ryzykowne walory A, B, C, charakteryzujące się stopami zwrotu ![]()
, oczekiwanymi stopami zwrotu ![]()
, ryzykiem ![]()
(i=A,B,C) i macierzą kowariancji stóp zwrotu:
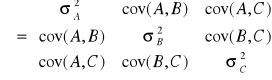
pamiętając przy tym, że kowariancja daje się przedstawić jako funkcja współczynnika korelacji ![]()
, tzn.
![]()
.
Wektor wag portfelowych, określający strukturę portfela, ma postać:
![]()
przy czym ![]()
.
Stopa zwrotu portfela trzyskładnikowego jest zdefiniowana jako:
![]()
,
natomiast jej oczekiwana wartość jako:
![]()
.
Ryzyko, mierzone wariancją stopy zwrotu, definiuje wzór:
![]()
.
Przypadek trzech walorów omawiamy dlatego, by pokazać, jak odczytywać na płaszczyźnie (ryzyko; dochód) różnie skonstruowane portfele, zbiory możliwych rozwiązań oraz krzywe rozwiązań efektywnych.
Rozważmy układ walorów ryzykownych A, B, C. Parametry ich rozkładów przedstawiamy w tablicy 18.
Tablica 18. Parametry rozkładu stóp zwrotu (w %)
Walor A |
Walor B |
Walor C |
|||
|
|
|
|
|
|
10 |
5 |
8 |
4 |
4 |
2,5 |
Źródło: opracowanie własne
Załóżmy, że dla rozpatrywanych walorów macierz kowariancji stóp zwrotu ma postać:
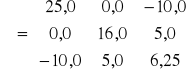
.
Pamiętając o zależnościach występujących między kowariancji a współczynnikami korelacji, możemy zapisać następującą macierz współczynników korelacji stóp zwrotu:
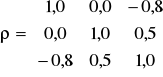
.
Zatem w naszym przykładzie występują zarówno walory skorelowane dodatnio, ujemnie jak i nieskorelowane.
Dla przykładu obliczmy oczekiwaną wartość portfela składającego się z walorów A, B i C o następującej strukturze: ![]()
![]()
![]()
. Otrzymujemy:
![]()
.
Ponieważ nie zachodzi krótka sprzedaż zatem oczekiwana wartość portfela nie może przekroczyć maksymalnej z wartości oczekiwanych składowych portfela.
Rozważmy portfel, w którym sprzedano krótko pewną ilość waloru C i dodatkowo zakupiono walor A, tak że wagi portfelowe są ![]()
![]()
![]()
. Wartość oczekiwana takiego portfela jest równa:
![]()
,
zatem portfel taki ma wartość oczekiwaną, która przekracza 10%.
Wariancja stopy zwrotu portfela o strukturze ![]()
![]()
![]()
jest równa:
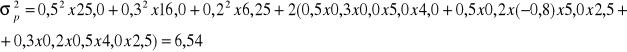
natomiast ryzyko mierzone odchyleniem standardowym stopy zwrotu:
![]()
.
Oznacza to, że zrealizowany zysk z inwestycji w portfel, o założonej wyżej strukturze, odchylać się może od oczekiwanego zysku równego 8,2% średnio rzecz biorąc in plus in minus o 2,56%.
Dla portfela z krótką sprzedażą otrzymujemy:
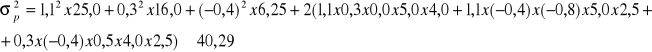
zaś ryzyko mierzone odchyleniem standardowym wynosi:
![]()
.
Oznacza to, że zrealizowany zysk z inwestycji w portfel z krótka sprzedażą, odchylać się może od oczekiwanego zysku równego 11,8% średnio rzecz biorąc in plus in minus o 6,35%.
W tablicy 19 przedstawiono obliczenia wartości oczekiwanych oraz odchyleń standardowych wybranych portfeli trzyskładnikowych leżących na granicy zbioru możliwych rozwiązań (bez krótkiej sprzedaży). Pogrubioną czcionką zaznaczono portfel o globalnie najmniejszej wariancji.
Tablica 19. Parametry rozkładu portfela trzyskładnikowego
|
|
|
|
|
0,00 |
0,00 |
1,00 |
4,00 |
2,50 |
0,32 |
0,00 |
0,68 |
5,90 |
1,05 |
0,39 |
0,00 |
0,61 |
6,36 |
1,18 |
0,43 |
0,06 |
0,51 |
6,81 |
1,49 |
0,45 |
0,14 |
0,41 |
7,27 |
1,83 |
0,47 |
0,23 |
0,30 |
7,72 |
2,18 |
0,48 |
0,32 |
0,20 |
8,18 |
2,54 |
0,50 |
0,41 |
0,09 |
8,63 |
2,90 |
0,54 |
0,46 |
0,00 |
9,09 |
3,28 |
0,77 |
0,23 |
0,00 |
9,54 |
3,97 |
1,00 |
0,00 |
0,00 |
10,00 |
5,00 |
Źródło: opracowanie własne
W tablicy 20 i 21 przedstawiono obliczenia wartości oczekiwanych oraz odchyleń standardowych portfeli dwuskładnikowych leżących na granicach zbiorów możliwych rozwiązań (bez krótkiej sprzedaży). Pogrubioną czcionką zaznaczono portfele o najmniejszej wariancji.
Tablica 20. Parametry rozkładu portfela dwuskładnikowego
zawierającego A i B
|
|
|
|
0,00 |
1,00 |
8,00 |
4,00 |
0,39 |
0,61 |
8,78 |
3,12 |
0,46 |
0,54 |
8,92 |
3,15 |
0,53 |
0,47 |
9,05 |
3,24 |
0,59 |
0,41 |
9,19 |
3,38 |
0,66 |
0,34 |
9,32 |
3,57 |
0,73 |
0,27 |
9,46 |
3,80 |
0,80 |
0,20 |
9,59 |
4,07 |
0,86 |
0,14 |
9,73 |
4,35 |
0,93 |
0,07 |
9,86 |
4,67 |
1,00 |
0,00 |
10,00 |
5,00 |
Źródło: opracowanie własne
Tablica 21. Parametry rozkładu portfela dwuskładnikowego
zawierającego B i C
|
|
|
|
0,00 |
1,00 |
4,00 |
2,50 |
0,10 |
0,90 |
4,41 |
2,47 |
0,20 |
0,80 |
4,81 |
2,50 |
0,30 |
0,70 |
5,21 |
2,57 |
0,40 |
0,60 |
5,61 |
2,69 |
0,50 |
0,50 |
6,00 |
2,84 |
0,60 |
0,40 |
6,40 |
3,03 |
0,70 |
0,30 |
6,80 |
3,24 |
0,80 |
0,20 |
7,20 |
3,48 |
0,90 |
0,10 |
7,60 |
3,73 |
1,00 |
0,00 |
8,00 |
4,00 |
Źródło: opracowanie własne
Rysunek 17 . Zbiór możliwości inwestycyjnych dla portfela złożonego z trzech walorów
![]()
14
13
12
11
10 A
9
N3
8 B
7
6 N1
5
4 N2
3 C
2
1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ![]()
Źródło: opracowanie własne
Dane zawarte w tablicach 19-21 naniesiono na rysunek 17. Krzywa ![]()
jest granicą efektywnych portfeli trzyskładnikowych (ABC), przy czym ![]()
jest portfelem o globalnie minimalnej wariancji. Krzywa ![]()
jest granicą efektywną portfeli dwuskładnikowych (BC), przy czym ![]()
jest portfelem o minimalnej wariancji. Z kolei krzywa ![]()
jest granicą efektywną portfeli dwuskładnikowych tworzonych z (AB), zaś ![]()
jest portfelem o minimalnej wariancji. Zatem figura ![]()
jest zbiorem portfeli dominujących nad wszystkimi innymi portfelami dwuskładnikowymi.
5.2. Portfel dla dowolnej liczby akcji
Wzory rozpatrywane w punktach poprzednich uogólnia się na dowolną liczbę akcji. Załóżmy, że rozpatrujemy K różnych walorów charakteryzowanych przez:
![]()
; ![]()
; ![]()
; ![]()
; ![]()
stopy zwrotu, oczekiwane stopy zwrotu, odchylenia standardowe oraz kowariancje.
Strukturę portfela opisują wagi ![]()
, spełniające:
![]()
.
Stopa zwrotu portfela jest kombinacją K stóp zwrotu poszczególnych walorów, zatem:
![]()
.
Podobnie oczekiwana stopa zwrotu jest kombinacją liniową oczekiwanych wartości poszczególnych stóp zwrotu:
![]()
.
Wariancja portfela jest dana przez:
![]()
.
Krzywe portfeli minimalnego ryzyka, zamieszczone na rysunkach 11 i 17 odpowiednio dla portfeli 2 i 3 elementowych, są graficznym rozwiązaniem tzw. modelu Markowitza. Model ten jest matematycznym sformułowaniem problemu wyboru inwestora niechętnego wobec ryzyka, który wybiera w kategoriach ryzyko-dochód. Model Markowitza pozwala na wyznaczenie takich wag portfelowych, które definiują portfel o założonej wartości oczekiwanego zysku i najmniejszym ryzyku.
Formalny zapis modelu dla sytuacji, kiedy nie jest dozwolona krótka sprzedaż, przedstawia się następująco:
wyznaczyć wagi portfelowe
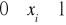
, takie że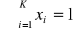
,takie, że oczekiwany zysk portfela wynosi
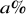
, tj.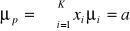
,dla którego wariancja stopy zwrotu portfela (miara ryzyka) jest najmniejsza
![]()
.
W przypadku, gdy możliwa jest krótka sprzedaż walorów na rynku wtedy wagi portfelowe mogą przybierać wartości nie tylko z przedziału ![]()
(mogą być również ujemne, większe od jedności). W takim przypadku w modelu nie występuje ograniczenie brzegowe ![]()
. Model ten rozwiązuje się metodami właściwymi dla nieliniowych zadań decyzyjnych (metodami programowania kwadratowego, bądź ogólną metodą Kuhna-Tuckera). Rozwiązaniem tak zapisanego modelu jest krzywa minimalnego ryzyka umieszczona na rysunku 11 lub 17.
Dla portfeli zawierających wiele różnych walorów można określić tzw. efekt dywersyfikacji ryzyka. Dywersyfikacja ryzyka jest to inaczej rozproszenie (zmniejszenie) ryzyka portfela na skutek włączenia doń dużej liczby różnych walorów bez obniżenia oczekiwanej stopy zwrotu portfela.
Rozważmy najpierw następującą sytuację: niech wszystkie stopy zwrotu walorów umieszczonych w portfelu są nieskorelowane, czyli ![]()
. Wtedy wariancja portfela redukuje się do:
![]()
.
Załóżmy ponadto, że inwestujemy w każdy walor tę samą sumę pieniędzy, zatem:
![]()
.
Wstawiając tę wielkość do wyrażenia na wariancję otrzymujemy:
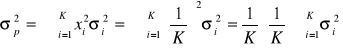
.
Wyrażenie:
![]()
średnią wariancją stóp zwrotu walorów uwzględnionych w portfelu. W konsekwencji
![]()
.
Jeśli ![]()
, wtedy ![]()
. Zatem, jeśli inwestor posiada dostatecznie rozbudowany portfel, składający się z niezależnych walorów, wariancja portfela zmierza do zera. W rzeczywistości stopy zwrotu różnych walorów są skorelowane (z reguły dodatnio).
Rozpatrzmy więc ponownie sytuację, gdy inwestor przeznacza równą kwotę na każdy walor ![]()
:
![]()
.
Wyłączając ![]()
oraz ![]()
z powyższej formuły zapiszemy:
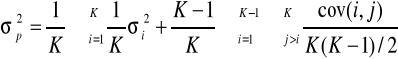
.
Wyrażenie w pierwszym składniku sumy po prawej stronie równania jest średnią wariancją, którą oznaczono jako ![]()
. Wyrażenie w drugim składniku sumy tego równania jest średnią kowariancją, którą oznaczymy jako:
![]()
.
Zatem ostatecznie wzór na wariancję zapiszemy:
![]()
.
Jeżeli liczba akcji w portfelu wzrasta, czyli ![]()
, wtedy wariancja portfela zmierza do średniej kowariancji, tj.:
![]()
.
Zatem nawet w przypadku bardzo dużych portfeli istnieje pewna ,,część'' ryzyka, którego nie można wyeliminować. Jest to ryzyko niedywersyfikowalne. Jest ono równe średniej kowariancji stóp zwrotu wszystkich walorów. Pokazuje to rysunek 18. Na rysunku tym ryzyko jest mierzone jako procentowy udział ryzyka portfela do oczekiwanego (przeciętnego) ryzyka portfela jednoskładnikowego.
Badania empiryczne dla rozwiniętych rynków kapitałowych dowodzą, że w miarę wzrostu liczby walorów w portfelu spadek jego ryzyka jest coraz mniejszy. Konstruując losowo wybrane portfele akcji składające się z 15-20 różnych walorów eliminowano około 90% ryzyka możliwego do wyeliminowania poprzez dywersyfikację.
Rysunek 18. Ryzyko a liczba walorów w portfelu
ryzyko
100
50
ryzyko kowariancyjne
2 4 6 8 10 12 14 16 18 20 22 24 26 ![]()
Źródło: opracowanie własne
W literaturze przedmiotu wyróżnia się szereg czynników (przyczyn) ryzyka systematycznego, wpływających na wszystkie walory notowane na rynku kapitałowym. Do najważniejszych czynników ryzyka systematycznego zalicza się:
zmiany koniunktury rynkowej,
zmiany podstawowych stóp procentowych w gospodarce,
zmiany (szczególnie nieoczekiwane) stopy inflacji,
zmiany tempa wzrostu PKB,
zmiany kursu waluty krajowej względem innych walut,
zmiany poziomu deficytu budżetowego (lub ogólnie zmiany poziomu długu wewnętrznego).
Do najważniejszych czynników ryzyka specyficznego zalicza się:
ryzyko działalności gospodarczej,
ryzyko finansowe.
Oba rodzaje ryzyka specyficznego wynikają ze specyficznych warunków w jakich emitent każdego papieru wartościowego prowadzi działalność gospodarczą. Ważny jest rodzaj rynku, na którym działa emitent (w szczególności udział w rynku, konkurenci, stosowane strategie marketingowe, posiadane sieci dystrybucji). Istotny jest poziom kadry zarządzającej przedsiębiorstwa, realizowane strategie rozwoju przedsiębiorstwa. Wreszcie ryzyko finansowe związane ze strukturą kapitałów wykorzystywanych w przedsiębiorstwie.
W punkcie 6 omówimy najprostszy jednoczynnikowy model ryzyka, tzw. model pojedynczego indeksu.
Wróćmy raz jeszcze do interpretacji linii rynku kapitałowego. Przypomnijmy, że ma ona postać:
![]()
.
Linia rynku kapitałowego dominuje bowiem wszystkie inne możliwości inwestycyjne w tym sensie, że:
- oferuje najwyższe oczekiwane stopy zwrotu dla danego poziomu ryzyka lub
- najmniejsze ryzyko dla danego poziomu oczekiwanej wartości stopy zwrotu portfela.
Wszyscy inwestorzy zatem będą zainteresowani jednym portfelem zawierającym walory ryzykowne i leżącym na tej linii, tj. portfelem M. Portfel rynkowy może być optymalnie łączony z walorem pozbawionym ryzyka F na odcinku FM. W punkcie M cały fundusz jest inwestowany w ten portfel. Na prawo zaś od niego dodatkowe fundusze pożyczone na procent równy stopie zwrotu wolnej od ryzyka są w ten portfel zainwestowane ![]()
.
Rysunek 19. Linia rynku kapitałowego (CML)
![]()
11
9 M
7
5
F
3
1
1 2 3 4 5 6 7 8 9 10 11 12 ![]()
Źródło: opracowanie własne
Można wobec tego zidentyfikować portfel ryzykowny, który wszyscy inwestorzy będą chcieli utrzymywać niezależnie od ich krzywych obojętności. Takim portfelem charakteryzującym wszystkich inwestorów niechętnych ryzyku jest portfel rynkowy. Jest to tzw. twierdzenie separacji Tobina. Inaczej mówiąc, inwestorzy o różnej tolerancji wobec ryzyka będą dostosowywać swoje własne portfele nie poprzez zmianę portfela rynkowego M na inny portfel ryzykowny, ale poprzez zmianę poziomu inwestowania w papiery wolne od ryzyka lub pożyczanie dodatkowych funduszy po stopie równej ![]()
. Inwestorzy będą więc poruszać się po linii rynku kapitałowego, nie zmieniając optymalnego portfela M, lecz zmieniając proporcje jego udziału w swoim portfelu.
Jeśli wszyscy inwestorzy dążą do utrzymania portfela rynkowego M, wtedy portfel ten musi zawierać wszystkie ryzykowne inwestycje, które są możliwe na rynku. Co więcej udział każdego waloru ryzykownego w portfelu rynkowym równa się udziałowi jego kapitalizacji w kapitalizacji rynku ogółem.
Portfel rynkowy istotnie wiąże się z cenami równowagi. Jeśli portfel rynkowy zawiera wszystkie walory notowane na giełdzie, wtedy ceny tych walorów muszą być takie, żeby można je było włączyć do portfela rynkowego. Inaczej mówiąc, ceny walorów są w równowadze, gdy generują one takie oczekiwane stopy zwrotu, które są wystarczającą rekompensatą za ryzyko, które jest z nimi związane.
Portfel rynkowy reprezentuje rynek, zatem musi być portfelem zdywersyfikowanym, tak, że zawiera ryzyko, które nie może być wyeliminowane. Dlatego rynkowa cena ryzyka 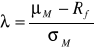
oznacza dodatkowy oczekiwany zysk (przekraczający zysk z papieru pewnego) będący premią za podjęcie każdego 1% ryzyka niedywersyfikowalnego (związanego z portfelem rynkowym M). Zatem inwestor nie może oczekiwać (od rynku) jakiejkolwiek premii z tytułu podjęcia ryzyka, które może być wyeliminowane przez dywersyfikację.
Na koniec warto podkreślić, że linia rynku kapitałowego nie dotyczy indywidualnych walorów (lub portfeli nieefektywnych). Dotyczy ona tylko portfeli efektywnych, konkretnie zaś portfela rynkowego.
6. Model pojedynczego indeksu
Najprostszym modelem opisującym zmiany stóp zwrotu różnych walorów w zależności od stopy zmian portfela rynkowego jest model pojedynczego indeksu zaproponowany przez Sharpe'a. W bardziej rozbudowanych modelach uwzględnia się większą liczbę czynników ryzyka systematycznego, o których mówiliśmy w poprzedniej części wykładu. W modelu Sharpe'a zakłada się występowanie liniowej zależności miedzy stopą zwrotu i-tego waloru a stopą zmian portfela rynkowego. Zapiszmy następującą relację:
![]()
![]()
gdzie: ![]()
- stopa zwrotu inwestycji w i-ty papier wartościowy, ![]()
- stopa zmiany portfela rynkowego, aproksymowana najczęściej przez stopę zmian agregatowego indeksu giełdowego, ![]()
- składnik losowy ujmujący wpływ innych, niż koniunktura giełdowa czynników na zmiany stopy zwrotu i-tego waloru, ![]()
- stały komponent stopy zwrotu niezależny od zmian indeksu giełdowego, ![]()
- współczynnik beta określający zmianę stopy zwrotu i-tego waloru spowodowaną przyrostem stopy zwrotu indeksu giełdowego o 1%. Parametr ![]()
określany jest jako miara ryzyka systematycznego
W modelu tym przyjmuje się zatem, że jedynym czynnikiem systematycznie wpływającym na wszystkie walory (czynnikiem ryzyka systematycznego) są zmiany koniunktury rynkowej. Składnik losowy ![]()
traktuje się tutaj jako zmienną ujmującą czynniki ryzyka specyficznego (charakterystyczne dla danego waloru).
Warto omówić kilka specjalnych przypadków określonych przez wartości przyjmowane przez współczynnik ![]()
. Jeżeli ![]()
, wówczas stopa zwrotu i-tego waloru nie zależy od zmian koniunktury giełdowej, lecz losowo odchyla się od stałej ![]()
. Jeżeli ![]()
, wówczas poprawie koniunktury na giełdzie mierzonej przyrostem tempa wzrostu indeksu giełdowego o 1% towarzyszy przyrost stopy zwrotu i-tego waloru o mniej niż 1%. W przypadku, gdy ![]()
stopa zwrotu z analizowanego waloru wzrasta w takim samym tempie jak indeks giełdowy. Jeżeli ![]()
, wtedy poprawa koniunktury giełdowej mierzona przyrostem tempa wzrostu indeksu giełdowego o 1% wywołuje przyrost stopy zwrotu i-tego waloru o więcej niż 1%. Ujemna wartość współczynnika ![]()
może być interpretowana jako przejaw kształtowania się stopy zwrotu wbrew tendencji panującej na rynku, czyli oznacza jej spadek o ![]()
w sytuacji poprawy koniunktury o 1%.
6.1 Założenia stochastyczne modelu pojedynczego indeksu
Zakłada się, że składniki losowe ![]()
mają następujące własności:
1. ![]()
- czyli losowo oscylują wokół zera,
2. ![]()
- czyli mają stałe wariancje,
3. ![]()
- czyli są nieskorelowane dla różnych walorów,
4. ![]()
- czyli są nieskorelowane ze stopą zmian indeksu giełdowego.
Ponadto zakładamy, że stopa zmian indeksu giełdowego ma następujące parametry rozkładu:
5. wartość oczekiwaną - ![]()
,
6. wariancję - ![]()
.
Przy tych założeniach parametry rozkładu stopy zwrotu i-tego waloru określone są przez parametry rozkładu indeksu giełdowego ![]()
i składnika losowego (niesystematycznego) ![]()
. Możemy zapisać, że:
7. ![]()
- oczekiwana wartość stopy zwrotu i-tego waloru jest liniową funkcją oczekiwanej wartości stopy zmian indeksu giełdowego.
8. ![]()
- wariancja stopy zwrotu i-tego waloru jest ważoną sumą wariancji indeksu giełdowego (ryzyko systematyczne) i wariancji czynnika losowego (ryzyko specyficzne dla tego waloru).
9. ![]()
; ![]()
- kowariancja pomiędzy stopami zwrotu dwóch różnych walorów.
Wykorzystując przyjęte założenia możemy zapisać, że parametry ![]()
oraz ![]()
dla i-tego waloru spełniają następujący układ równań:
![]()
,
![]()
,
gdzie: ![]()
jest kowariancją pomiędzy stopą zmian i-tego waloru a stopą zmian indeksu giełdowego, ![]()
jest natomiast współczynnikiem korelacji pomiędzy wymienionymi wyżej stopami zmian.
Wartość współczynnika ![]()
zależy zatem od siły i kierunku skorelowania stopy zwrotu i-tego waloru ze stopą zmian indeksu giełdowego oraz zmienności stopy zwrotu i-tego waloru w stosunku do zmienności indeksu .
6.2 Empiryczna wersja modelu pojedynczego indeksu
Próbkową wersją modelu pojedynczego indeksu jest:
![]()
![]()
gdzie: ![]()
, ![]()
oznaczają zaobserwowane w przeszłości stopy zwrotu, ![]()
oznacza zakłócenie losowe w okresie t, natomiast T oznacza liczebność obserwacji np. liczbę sesji z których pochodzą obserwacje.
Próbkowymi ocenami parametrów rozkładów stóp zwrotu są:
- średnie z próby: ![]()
, ![]()
,
- wariancje z próby: ![]()
, ![]()
,
- kowariancja z próby: ![]()
,
- współczynnik korelacji z próby: 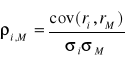
.
Współczynniki ![]()
, ![]()
szacowane są metodą najmniejszych kwadratów za pomocą zgodnie z:
![]()
,
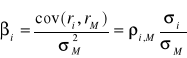
.
Oceną wariancji składników losowych (ryzyka specyficznego) jest wariancja reszt, obliczana zgodnie z:
![]()
,
gdzie ![]()
jest resztą z oszacowania modelu.
Oceny parametrów ![]()
, ![]()
zapisane powyżej obarczone są błędami. Wariancje błędów ocen tych parametrów, które oznaczać będziemy ![]()
, ![]()
, są wyznaczane według wzorów zapisanych w przypisie. Pierwiastki z tych wariancji
![]()
, ![]()
określamy jako średnie błędy szacunku parametrów. Określają one dokładność z jaką na podstawie obserwacji oszacowano nieznane parametry ![]()
oraz ![]()
.
Oszacowania parametrów modelu pojedynczego indeksu na podstawie 15 zaobserwowanych stóp zwrotu 8 akcji notowanych na GPW w Warszawie (dane zawarte w tablicy 8) przedstawiono w tablicy 22. Jako przybliżenie portfela rynkowego przyjęto portfel WIG (warszawskiego indeksu giełdowego), zatem ![]()
.
Zauważmy, że oceny parametru ![]()
dla rozpatrywanych akcji są bardzo zróżnicowane, od bliskich zera do bliskich jedności. Oceny parametrów obarczone są dużymi błędami. W dużej części jest to wynik tego, że do oszacowania wzięto dane sesyjne. Oszacowania dla tygodniowych bądź miesięcznych stóp zwrotu obarczone są mniejszymi błędami. Zinterpretujemy obecnie oszacowania parametru ![]()
dla dwóch wybranych akcji tj. np. Agrosu i Amica.
Tablica 22. Oszacowania parametrów modelu pojedynczego indeksu dla wybranych akcji
Ocena
|
ragros |
rambank |
ramica |
rampli |
rams |
ranimex |
rapator |
rapexim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Źródło: opracowanie własne
Na podstawie oszacowania tego parametru dla Agrosu równego ![]()
, stwierdzamy, że wzrost koniunktury giełdowej o 1%, powodował przeciętnie wzrost stopy zwrotu inwestycji w akcje Agrosu o 0,143% z błędem ![]()
0,086%.
Na podstawie oszacowania tego parametru dla Amica równego ![]()
, stwierdzamy, że wzrost koniunktury giełdowej o 1%, powodował przeciętnie wzrost stopy zwrotu inwestycji w akcje Amica o 0,995% z błędem ![]()
0,164%.
7. Model wyceny kapitału (CAPM)
Kluczowym dla zrozumienia modelu CAPM jest pojęcie rynku w równowadze (rynku doskonałego). Rynek ten definiuje się poprzez przyjęcie szeregu założeń, określających sposób działania i strukturę rynku oraz sposób postępowania inwestorów na nim. Wymieńmy najważniejsze z tych założeń:
istnieje skończona liczba doskonale podzielnych walorów, co znaczy że można sprzedawać dowolne wielkości walorów, w tym również ułamkowe,
rynek walorów jest jednorodny, tzn. każdy walor może być w sposób płynny zamieniony na pieniądz, cena pieniądza jest wyznaczana przez stopę wolną od ryzyka,
indywidualny inwestor nie może wpłynąć na cenę waloru poprzez swoje decyzje inwestycyjne (zakupu lub sprzedaży),
inwestorzy podejmują decyzje uwzględniając dwa parametry: wartość oczekiwaną swojego bogactwa (stopy zwrotu bogactwa) oraz jego odchylenie standardowe (ryzyko). Inwestorzy są niechętni wobec ryzyka i dążą do maksymalizacji oczekiwanej użyteczności swojego bogactwa.
informacja odnośnie do stanu rynku jest bezpłatna,
inwestorzy mają jednakowe (homogeniczne oczekiwania) ze względu na zbiór informacji wykorzystywany do podejmowania decyzji inwestycyjnych.
W rzeczywistości rynki finansowe nie znajdują się nigdy w stanie idealnej równowagi. W przypadku każdego z przyjętych wyżej założeń można postawić pytanie: na ile warunki konkretnego rynku finansowego odbiegają od założeń idealnych? Przy pomocy model CAPM wyznaczamy cenę każdego waloru w sytuacji, gdy rynek jest w równowadze. W rzeczywistości zatem, na skutek tego, że rynki finansowe nie spełniają wszystkich założeń, wycena poszczególnych walorów zawierać będzie pewne odchylenia od cen równowagi.
Można udowodnić, że w warunkach równowagi, kiedy wszyscy inwestorzy wybierają portfele znajdujące się na linii rynku kapitałowego, stopy zwrotu poszczególnych portfeli ryzykownych (w tym również pojedynczych walorów) są wyznaczane przez:
![]()
gdzie: ![]()
jest oczekiwaną stopą zwrotu inwestycji w portfel ryzykowny w warunkach równowagi, ![]()
jest stopą wolną od ryzyka, ![]()
jest współczynnikiem ryzyka systematycznego (zobacz model pojedynczego indeksu), natomiast ![]()
jest oczekiwanym zyskiem portfela rynkowego.
Zatem współczynnik ![]()
decyduje o tym, jaką część premii za ryzyko rynku stanowi premia za ryzyko z tytułu inwestycji w portfel ryzykowny. Można bowiem zapisać, że ![]()
. Obrazem graficznym równania CAPM jest linia rynku papierów wartościowych (SML). Jest ona ściśle związana z linią rynku kapitałowego (CML), co pokazują rysunki 20.a-20.b. Różnica pomiędzy wspomnianymi wyżej prostymi polega na tym, że linia rynku kapitałowego przedstawia liniową zależność pomiędzy oczekiwanym zyskiem a ryzykiem całkowitym, mierzonym odchyleniem standardowym portfela![]()
, natomiast linia rynku papierów wartościowych przedstawia liniową zależność pomiędzy oczekiwanym zyskiem a ryzykiem systematycznym, mierzonym ![]()
![]()
.
Model równowagi CAPM jest ściśle powiązany z empirycznym modelem pojedynczego indeksu, omawianym w punkcie poprzednim. Pokazaliśmy, że jeśli spełnione są założenia stochastyczne tego modelu, wtedy oczekiwana wartość stopy zwrotu rozpatrywanego waloru jest równa:
![]()
.
Z drugiej strony wycena tego waloru w warunkach równowagi, zgodnie z CAPM, daje:
![]()
.
Z równości zapisanych wyżej wynika, że:
![]()
.
Zatem jeśli ![]()
, wtedy ![]()
, czyli walor o zerowym współczynniku ![]()
oferuje oczekiwaną stopę zwrotu na poziomie stopy zwrotu wolnej od ryzyka. Ponadto, jeśli ![]()
, wtedy ![]()
, co znaczy, że walor charakteryzujący się takim samym jak portfel rynkowy współczynnikiem ![]()
, oferuje taką samą jak ten portfel oczekiwaną stopę zwrotu (![]()
.
Rysunek 20a. Linia rynku kapitałowego Rysunek 20b. Linia rynku papierów wartościowych
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Źródło: opracowanie własne
Literatura.
Adams A., D. Bloomfield, P. Booth, P. England, Investment Mathematics and Statistics, Graham & Trotman, London 1993.
Bołt T.W., P. Miłobędzki, Materiały szkoleniowe z Analizy Portfelowej, Gdańska Akademia Bankowa, Gdańsk 1994.
Bołt T.W., P. Miłobędzki, Empiryczna analiza procesów zachodzących na Warszawskiej Giełdzie Papierów Wartościowych w latach 1991-1993, Materiały Studialne nr 2, Gdańska Akademia Bankowa, Gdańsk 1994.
Bronsztejn L.N., K.A. Siemiendiajew, Matematyka. Poradnik encyklopedyczny, PWN, Warszawa, 1986.
Elton E.J., M.T. Gruber, Nowoczesna teoria portfelowa i analiza papierów wartościowych, WIG Press, Warszawa 1998.
Freund J.E., Podstawy nowoczesnej statystyki, PWE, Warszawa 1968.
Grabowski W., Programowanie matematyczne, PWE, Warszawa 1980.
Haugen R.A., Teoria nowoczesnego inwestowania, WIG Press, Warszawa 1996.
Hellwig Z., Elementy rachunku prawdopodobieństwa i statystyki matematycznej, PWN, Warszawa 1970.
Jajuga K., Zarządzanie kapitałem, Wydawnictwo AE we Wrocławiu, Wrocław 1993.
Jajuga K., T. Jajuga., Jak inwestować w papiery wartościowe, PWN Warszawa 1994.
Lumby S., Investment Appraisal and Financial Decisions, Chapman & Hall, London 1994.
Luszniewicz A., Statystyka ogólna, PWE, Warszawa 1975.
Sharpe W., Mean-Absolute-Deviation Characteristic Lines for Securities and Portfolios. Management Science, 1971, tom. 18, nr. 2, str. B1-B13.
Skrypt pt. Rynki finansowe, zawiera materiał potrzebny do zaliczenia przedmiotu ,,Rynki finansowe'', prowadzonego przez dr hab. Tadeusza W.Bołta. Materiał opracowano na podstawie wykładów autora oraz literatury przedmiotu podanej na końcu. Skrypt ten nie może być traktowany jako jedyne źródło wiedzy z przedmiotu!
Można udowodnić, że kowariancja zawiera się w przedziale ![]()
.
Zob. np. E.J.Elton, M.J.Gruber, Nowoczesna teoria portfelowa i analiza papierów wartościowych, WIG Press, Warszawa, 1998, str. 3-11.
Teoria zachowania konsumenta jest omówiona np. w książce: D. Begg, S. Fisher, R. Dornbusch, Ekonomia, PWE, Warszawa 1993, t. 1, rozdz. 5.
Formalne wyprowadzenie funkcji użyteczności z własności relacji preferencji można znaleźć np. w pracy: H.R. Varian, Microeconomic Analysis, New York 1984, s. 111-115.
W przypadku, gdy rozpatrujemy ciąg dochodów w n latach możemy zapisać (zakładając stałą stopę dyskontową), że: ![]()
. W bardziej ogólnym przypadku możemy rozpatrywać zmienne stopy procentowe ![]()
. Bogactwo inwestora możemy, równoważnie, wyrazić w kategoriach wartości bieżącej ciągu dochodów (konsumpcji).
Jeżeli ![]()
jest zmienną losową, to również użyteczność tego dochodu jest zmienną losową.
Zob. np. L.N.Bronsztejn, K.A.Siemiendiajew, Matematyka. Poradnik encyklopedyczny, PWN, Warszawa, 1986, str. 642.
W przypadku, gdy funkcja użyteczności jest kwadratowa względem dochodu/stopy zwrotu, wtedy przybliżenie jest dokładne.
Różniczka ta jest równa zeru, gdyż obliczamy ją dla ustalonego poziomu użyteczności.
O tym w jaki sposób znaleźć wagi takiego portfela opowiemy w następnych częściach wykładu.
Zob. np. W.Grabowski, Programowanie matematyczne, PWE, Warszawa 1980.
Zob. S. Lumby, Investment Appraisal and Financial Decisions, Chapman & Hall, London 1994, str. 258-259.
W. Sharpe, Mean-Absolute-Deviation Characteristic Lines for Securities and Portfolios. Management Science, 1971, tom. 18, nr. 2, str. B1-B13.
Portfel rynkowy, jak mówiliśmy w poprzedniej części wykładów, nie jest bezpośrednio obserwowalny. Zawiera on w sobie wszystkie aktywa będące przedmiotem transakcji na rynku. Struktura portfela rynkowego odtwarza strukturę rynku w tym sensie, że udział danego waloru w portfelu rynkowym jest taki, jak udział kapitalizacji tego waloru w kapitalizacji rynku. Zmiany wartości portfela określają zmiany koniunktury na rynku. Jako przybliżenia portfela rynkowego przyjmuje się zwykle agregatowe indeksy giełdowe, których zadaniem jest mierzenie koniunktury na tym rynku.
Wariancje błędów ocen wyznacza się wykorzystując założenia stochastyczne modelu. Określają one średni kwadratowy błąd oszacowania nieznanego parametru i mają postać: 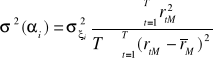
oraz 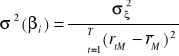
.
Tadeusz W.Bołt, Rynki finansowe, część II, rok akademicki, 2004/2005
58
Wyszukiwarka
Podobne podstrony:
zarządzanie inwestycjami kapitałowymi wykład 6
Inwestycje kapitalowe [ ściąga], inwestycje pkt 5, Pyt
Bankowość II, Inwestycje kapitałowe banków
INWESTYCJE KAPITAŁOWE wnioski1
Inwestycje kapitałowe, inwestycje-3,4, * John Murphy - guru (rewolucjonista
Inwestycje kapitalowe [ ściąga], inwestycje pkt 4, Pyt
zarządzanie inwestycjami kapitałowymi - wykład 4, Zarządzanie(1)
Inwestycje kapitałowe, wykład, * John Murphy - guru (rewolucjonista
Inwestycje kapitałowe banków, Finanse
zarządzanie inwestycjami kapitałowymi - wykład 5, Zarządzanie(1)
inwestycje kapitałowe, NAUKA, [Rynek Kapitałowy]
więcej podobnych podstron