TWÓJ BIOTECHNOLOG https://www.facebook.com/twoj.biotechnolog

Ćwiczenie 54: Badanie zjawiska rezonansu elektromagnetycznego.

1. Cel ćwiczenie:

1. Zapoznanie się ze zjawiskiem rezonansu elektromagnetycznego w szeregowym obwodzie drgającym RLC

2. Wykreślenie krzywych rezonansowych I = I(f)

3. Wyznaczenie częstotliwości rezonansowych obwodu w krzywych rezonansowych i przy pomocy oscyloskopu

4. Wyznaczenie współczynnika dobroci obwodu

2. Wstęp teoretyczny:

Prądem przemiennym nazywamy prąd o okresowo zmieniającym się w czasie natężeniu i kierunku prądu. Najczęściej stosuje się prąd o wartościach natężenia i napięcia zmieniających się sinusoidalnie w czasie.

Jeżeli w obwodzie ze źródłem napięcia przemiennego zmieniającego się w czasie według wzoru: u = U_osinωt występuje tylko opornik o oporze czynnym R, to natężenie prądu w obwodzie zmienia się według i_R = I_Rsinωt , gdzie I_R = U_o/R .

Wielkości u, i_R oznaczają wartości chwilowe napięcia i natężenia U_0, I₀ - amplitudy

ω = częstość kołowa powiązana z częstotliwością f wzorem ω = 2πf.

Jeżeli obwód zawiera jedynie źródło napięcia zmiennego i kondensator o pojemności C, to natężenie prądu płynącego w obwodzie zmienia się według równania:

i_C = I_Csin(ωt+π/2), gdzie I_C =ωCU₀.

Jeżeli natomiast elementem obwodu zmiennego będzie cewka o indukcyjności L, to w obwodzie płynie prąd przemienny i_L = I_Lsin(ωt- π/2), gdzie I_L =U­₀/ ωL.

Te zależności są słuszne dla obwodów, przez które przepływają prądy o niskiej częstotliwości. Wtedy elementy R, L, C można traktować jako idealne, tzn. takie, które mają wyłącznie opór czynny R, opór indukcyjny X_L = ωL i opór pojemnościowy

X_C = 1/ωC.

Dla obwodów szeregowych o napięciu przemiennym u = U_osinωt złożonych z rezystora o oporze R, cewki indukcyjnej o indukcyjności L i kondensatora o pojemności C opór R jest sumą oporu cewki indukcyjnej i oporu czynnego opornika.

Natężenie wyraża się wzorem i = I₀sin(ωt+φ), gdzie φ - przesunięcie fazowe między natężeniem prądu i przyłożonym napięciem, dla którego

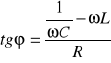
Prawo Ohma dla prądu przemiennego: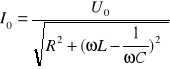

W obwodzie istnieje taki stan, że przy częstotliwości źródła napięcia

, gdzie ω_r - częstość rezonansowa

wtedy opór pojemnościowy X_C zrównuje się z oporem indukcyjnym X_L, amplituda I₀ natężenia prądu w obwodzie osiąga maksimum, a zawada układu minimum.

Kąt przesunięcia fazowego φ jest wtedy równy 0. Zjawisko to nosi nazwę rezonansu elektromagnetycznego szeregowego (rezonansu napięć).

Współczynnik dobroci układu określa wzór:

Schemat układu pomiarowego:

3. Przebieg pomiarów i przykładowe obliczenia:

	C [nF]	fr [kHz]	f1 [kHz]	f2 [kHz]	L [H]	Q
1	63,7	5,98	3,76	3,98	0,011±0,000779	27,18 ± 0,54
2	17,64	3,875	5,86	6,1	0,096±0,006701	16,15 ± 0,32
3	9,31	2,675	2,59	2,79	0,38±0,026643	13,38 ± 0,27

Wartości f_r, f₁ oraz f₂ zostały odczytane z wykresów.

Dla R3+C1

Imax = 17,2 [mA]

Imax /
= 12,16 [mA]

Dla R3+C2

Imax = 19,38 [mA]

Imax /
= 13,7 [mA]

Dla R3+C3

Imax = 20,88 [mA]

Imax /
= 14,76 [mA]

Wyznaczanie indukcyjności cewki:

Po przekształceniu otrzymujemy:

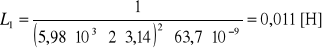
∆C = ±5%

∆fr = ±1%

∆C₁ = 3,19∙10^-9 [F]

∆fr₁ = 59,8 [Hz]

[H]

δL₁= (
/0,011)*100% = 7%

L₁ = 0,011 ± 7,79*10^-4 [H]

Obliczanie współczynnika dobroci:

Q₁=

f₂ - f₁= ∆f

lnQ = lnfr - ln(∆f)

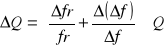
δQ₁= (0,54/27,18)*100% = 2%

Q₁ = 27,18 ± 0,54

4. Wnioski:

• Współczynnik dobroci obwodu rośnie wraz ze wzrostem wartości pojemności C

• Indukcyjność cewki L maleje wraz ze wzrostem wartości pojemności C

• Im większa wartość pojemności C tym większa częstotliwość rezonansowa fr

• Niepewności pomiarowe są związana z niedokładnością urządzeń, z których korzystałam podczas wykonywania ćwiczenia. Dla indukcyjności cewki we wszystkich przypadkach błąd względny wynosi 7%, a dla współczynnika dobroci 2%.

---