m Kolokwium I rok 2007/2008

Zadanie 1 : Zbadać, czy pole wektorowe
spełnia warunek wystarczający istnienia potencjału i wyznaczyć ten potencjał.

Rozwiązanie:

Warunek konieczny aby istniał potencjał w polu wektorowym

Jeżeli pole
jest potencjalne w swej dziedzinie, to
dla każdego

1. Sprawdzamy istnienie pola potencjalnego poprzez zbadanie rotacji

rot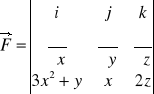

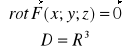
jest polem potencjalnym

2. Szukamy potencjału

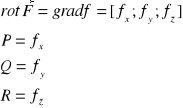
- obustronnie liczymy pochodną po y

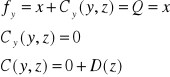
- obustronnie całkujemy po y

- obustronnie liczymy pochodną po z

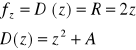
- potencjał pola wektorowego

Odp. Potencjał pola wektorowego wynosi

3. Aby sprawdzić poprawność rozwiązania liczymy gradient f, jeśli wyjdzie
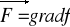
   oznacza on poprawnie policzony potencjał pola wektorowego i koniec zadania.

Odpowiedź: Potencjał pola wektorowego wynosi

Autor: Anna B. grupa 2