Zad 2
a) Oblicz odległość między płaszczyznami ∏1: 2x-y+3z=0 ∏2:-6x+3y-9z+1=0
b) Oblicz odległość punktu P=(1,-2,3) od płaszczyzny ∏:2x+2y-6z+10=0
Zad3.
Oblicz granice podanych ciągów:
2·2n - 3n+2
a)lim --------------- b) lim pierwiastek n-tego stopnia z (22n + ∏n + 3n)
n→∞ 3n+2 + 7 n→∞
4 n -3 n
c)lim ------------ d) lim pierwiastek n-tego stopnia z (22n + 6n + 123)
n→∞ 5 n -4n n→∞
(Podpunkty b i d metodą trzech ciągów)
Zad4.
Zbadaj ciągłość podanych funkcji:
a) f(x) {1+x2 , x≥0
{ -x2+1, x<0
b) f(x) {1/x , xЄ (1, ∞)
{ x , xЄ (-∞, 1>
Zad.5
Obliczyć pochodne funkcji:
Sin2x
a) f(x)= ---------------------
2 Pierwiastki z x
1+ tgx
b) f(x)= ---------------------
1- tgx
cos2x
c) f(x)= -----------------------------
Pierwiastek 3 stopnia z (x+1)
d) f(x)= arc tg (x + pierwiastek z x)
ROZWIĄZANIA
Zad2a. Na płaszczyźnie P1 wybieram dowolny punkt: A=(-1; 1; 1) i obliczam jego odległość od płaszczyzny P2: 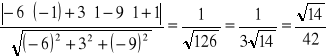
Zad2b. 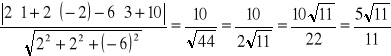
Zad3a. 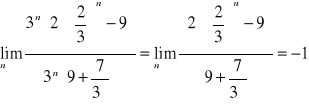
3b. ![]()
![]()
![]()
Zatem; ![]()
Zad3c. ![]()
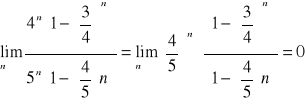
Zad3d. ![]()
![]()
![]()
Zatem: ![]()
Zad4a
![]()
![]()
Zatem: ![]()
oraz f(0) = 1+02 = 1 Zatem funkcja jest ciągła
Zad4b
![]()
![]()
Zatem ![]()
oraz f(1)=1 zatem funkcja jest ciągła
Zad5:
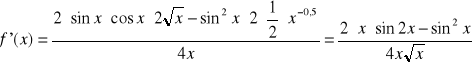
Zad5b
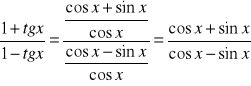
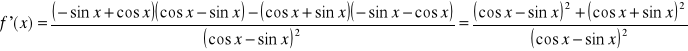
![]()
Zad5c.
![]()
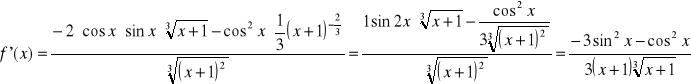
Zad5d.
![]()
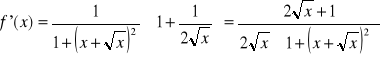
Wyszukiwarka
Podobne podstrony:
ŚCIĄGA NA 1 KOLOKWIUM, SGGW Technika Rolnicza i Leśna, Eksploatacja techniczna
MATMA (sciąga - macierze, Technika Rolnicza i Leśna, Semestr 1, Matematyka
Sprawozdanie [4]- Twardosc wody, Technika Rolnicza i Leśna, Semestr 1, Chemia i Materiałoznawstwo, S
Analiza jakościowa kationów i anionów, Technika Rolnicza i Leśna, Semestr 1, Chemia i Materiałoznaws
badania makroskopowe struktur surówek i żeliw, Technika Rolnicza i Leśna, Semestr 1, Chemia i Materi
Sprawozdanie chemia, Technika Rolnicza i Leśna, Semestr 1, Chemia i Materiałoznawstwo, Sprawozdania
sprawozdanie chemia5, Technika Rolnicza i Leśna, Semestr 1, Chemia i Materiałoznawstwo, Sprawozdania
CHEMIA III, Technika Rolnicza i Leśna, Semestr 1, Chemia i Materiałoznawstwo, Sprawozdania (chemia)
Sprawozdanie [2] - Stezenia, Technika Rolnicza i Leśna, Semestr 1, Chemia i Materiałoznawstwo, Spraw
kolokwia z automatyki, SGGW Technika Rolnicza i Leśna, Automatyka
REGULATOR PID, SGGW Technika Rolnicza i Leśna, Automatyka, Sprawozdania
IDENTYFIKACJA OBIEKTU, SGGW Technika Rolnicza i Leśna, Automatyka, Sprawozdania
nom pytaniahhhh, SGGW Technika Rolnicza i Leśna, NOM
Sprawozdanie Grupa 4, SGGW Technika Rolnicza i Leśna, MS
pytania i odpowiedzi na egzamin, SGGW Technika Rolnicza i Leśna, NOM
Sprawko 02, SGGW Technika Rolnicza i Leśna, Inżynieria elektryczna
więcej podobnych podstron