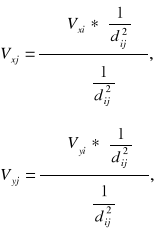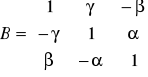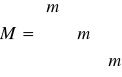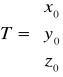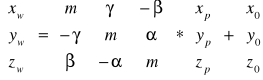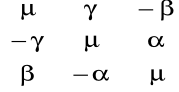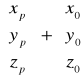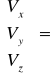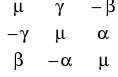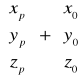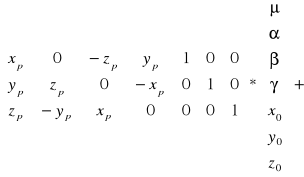Zad 1 Podaj pierwszy wyraz wzoru na γ z wykorzystaniem B i L

γ = lsinB, gdzie: l = L-L₀, L₀ to długość geodezyjna południka osiowego, L dl geodezyjna punktu, B szer geo punktu.

Zad 2 Korekta posttransformacyjna Hausbrandta.

Współrzędne otrzymane z transformacji według wzorow (X' = X₀ + C * x + S * y; Y' = Y₀ + C * y - S * x) nie musza się pokrywac z analogicznymi współrzędnymi punktow dostosowania, które jko wielkości dane służyły do wyznaczenia współczynników (parametrow) transformacji. O rozbieżności w tym zakresie świadczą wielkości poprawek, obliczne wzorami (V_xi = X_i - X_i^'; V_yi = Y_i - Y_i^'). Aby nie zmieniac dotychczasowych danych jako archiwalnych Hausbrandt zaproponował pewnego rodzaju dodatkowe,, uzgodnienie” współrzędnych, zwane korekta posttransformacyjna. Polega ona na tym ze współ punktow dostosowania w układzie wtornym pozostawia się w takiej postaci, w jakiej były przyjęte do transformacji, natomiast wszystkim pozostałym punktom transformowanym przyporzadkowuje się poprawki wyznaczone przy zastosowaniu specjalnych wzorow interpolacyjnych.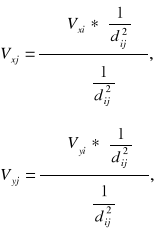

W ten sposób nastepuje swiadome deformacje wynikow trans Helmerta.

Powyższe wzory sa podobne do wzorow na obliczenie średnich wazonych, gdy wagi sa odwrotnosciami kwadratow odległości danego punktu o wskaźniku j (w zbiorze wszystkich punktow transformowanych) od punktu dostosowania o wskaźniku i (w zbiorze punktow dostosowania).

Jest to opisane w instrukcji technicznej G - 1.10 na 81 stronie.

Zad 3

1μgal = 10^-6gala = 10^-6cm*s^-2 = 10^-8m*s^-2 ( zadanie na kolokwium troche sie roznilo, nie pamietam dokladnej tresci, ale schemat jest ten sam.)

Zad 4

Wysokość na elipsoidzie Krasowskiego H_k = H_n

Wysokość na elipsoidzie GRS 80 H_g = H_n + 34,3 m

H_n - wysokość normalna (z mapy)

Zad 5

Rozwinac w szereg w otoczeniu punktu P różniczkę: (dl/ds.)_p

Wzor na to zadanie jest na 55 stronie w Czarneckim, wzor numer 2.59 (drugi w kolejności).

UWAGA!!! W tych wzorach sa bledy! Zamiast (L_m-L) w drugim wzorze i (A_m-A) w trzecim wzorze powinno być (B_m-B). To jest sprawdzone bo powiedział tak sam prof. Czarnecki.

Mysle ze nie powinno być problemow z opisaniem tego wzoru, wszystko jest w książce.

Zad6

Elipsoida ekwipotencjalna (Barlik str 71):

- srodek elipsoidy musi się pokrywac ze srodkiem Ziemi, a os jej głównego momentu bezwladnsci C musi być identyczna z osia obrotu Ziemi

- prędkość obrotu elipsoidy poziomowej i Ziemi musibyc taka sama

-masy obydwu bryl powinny być identyczne, lub ogólniej GM_el = GM_Z

-strefowe współczynniki harmoniczne drugiego stopnia w rozwinieciu w szereg potencjalu normalnego i potencjalu sily ciężkości Ziemi powinny być rowne J₂^el = J₂^Z

-normalny potencjal U₀ na powierzchni elipsoidy poziomowej powinien być rowny rzeczywistemu potencjałowi W₀ geoidy w punkcie wyjściowym sieci niwelacyjnych.

Zad 7

Co to jest Etwesz?

1E = 1mgal/10km = 10^-9s^-2 Etwesz jest jednotka gradientu przyspieszenia (zmiany przyspieszenia na jednostke wysokości)

Zad 8

Scharakteryzowac Sferoide normalna.

Podobno ktos zmaksowal to zadanie, odpowiedz za jakis czas powinna się pojawic na gronie geodezji.

Zad 9

wzor na przyciąganie nad kula: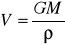
ρ- ro (odległość od srodka kuli do punktu, czyli w tym przypadku R + H)

Wzor na gradient wewnątrz kuli: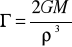
co do tego wzoru to nie jestem pewien.

Zad 10

Przyspieszenie na wysokości H nad elipsoida:

(Wzor jest w Czarneckim na stronie 115 - 3.103)

Trzeba tu oprocz opisania wielkości napisac, ze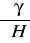
to gradient przyspieszenia.

Zad 11

Policzyc dziennik grawimetryczny.

Opisywac tego chyba nie musze

Zad 12

Dany jest pomiar przysp pod pow morza, należy zredukowac wynik na poziom geoidy.

trzeba zastoaowac redukcje Poincarego Preya, czyli skorzystac ze wzoru 5.45b na stronie 202 w Czarneckim.

Zad 13

Zredukowac pomierzona długość miedzy punktami 1-2 do układu 2000 majac dane:

500m - pomierzona długość. ΔH = 0 H = 800m A = 0⁰00^'00^”

oraz współrzędne x i y pierwszego punku.

Z danych wnioskujemy ze y₁ = y₂ (bo A=0)

Pomierzona długość (500m) należy zredukowac z tw. Talesa na pl G-K używając proporcji: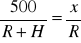
gdzie x to odległość na pl G-K

Jeśli dane współrzędne punktu początkowego sa na pl G-K to znajdujemy wspol x₂ (dodając długość na pl G-K do współrzędnej x₁) i przechodzimy z nimi do ukl 2000 i ze wspolrzednych liczymy odległość.

Jeśli dane współrzędne punktu początkowego sa na pl ukl 2000 to należy je odcechowac na pl G-K policzyc brakujaca wspolrzedna x₂ i wrócić ze współrzędnymi do ukl 2000, policzyc odległość.

Nie wiem czy to samo się osiągnie mnożąc po prostu odległość na pl G-K przez skale układu 2000.

To rozwiązanie jest tylko moim pogladem na te kwestie i nie wiem czy tok rozumowania jest poprawny.

Zad 14

Należy narysowac trojkat biegnowy.

Zad 15

Transformacja Bursy Wolfa

Nie pamiętam co trzeba bulo napisac, napisze wiec wszystko (dla grupy I, której Margan nie dal tych kartek z ta transformacja).

Macierz obrotow:

Macierz zniekształceń:

Wektor przesuniecia:

Postac ogolna funkcji transformującej:

X_w = BMX_p + T

Nie wyznaczamy współczynnika skali m, ale samo μ, wiec:

=
₊
*
, bo m = 1+μ

Równania poprawek:

*
+
-
=

-

Układ równań normalnych i jego rozwiązanie:

A^TAX + A^TL = 0

X = -(A^TA)^-1 * A^TL

To wszystko co było na kartce od Margana o tej transformacji.

sferoida normalna- pow ekwipotencjalna potencjalu sil ciezkosci Ziemi o potencjale Uo rownym potencjalowi geoidy Wo, opisana wzorem przedstawiajacym rozwiniecie potencjalu grawitacyjnego w szereg harmonicznych sferycznych z pominieciem tych wyrazow, ktore odpowiadaja symetrycznemu rozkladowi masy wzgl rownika, i wzgl osi obrotu (harmonicznych strefowych parzystych) i uzupelniony wyrazeniem opisujacym potencjal sily odsrodkowej U2n(r,Q)=Wo=const wyrozniamy sferoide 2go rzedu-Brunsa i 2go i 4go Helmerta
odl sferoidy helmerta od heoidy wynosi:
h=6,77 wg Lederstegera i h=2,78 wg Zabka
na pow sferoidy rzutujemy wielkosci dynamiczne np. przyspieszenie

---