Podstawy Fizyki Materii Skondensowanej, III rok

Zadania dla wszystkich grup - zestaw VI

dostępne również pod adresem: http://www.if.uj.edu.pl/pl/edukacja/pfms/

1. Model Einsteina

Oblicz
przyjmując
, gdzie N-liczba atomów w krysztale. Dla
pokaż, że 
spełnia prawo Dulonga-Petita.

2. Model Debye'a

a) Pokaż, że dla N atomów w sześcianie o boku L, gęstość stanów w przestrzeni pędów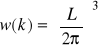
. Używając zależności dyspersyjnej
pokaż, że
dla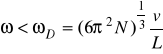
.

Oblicz
i pokaż, że dla

.

b) Jakie będzie ciepło właściwe
w niskich temperaturach dla magnonów (fal spinowych) w antyferromegnetyku opisanych liniową relacją dyspersji
(
)? Cząstki te podlegają statystyce Bosego-Einsteina.

3. Ciepło właściwe dla magnonów w ferromagnetyku

Przyjmując, że dla magnonów w ferromagnetyku liczba stanów o wektorze falowym mniejszym od
wynosi
a zależność dyspersyjna
oblicz gęstość stanów
a następnie
. Pokaż, że dla

.

---