Andrzej Karaś		dr Piotr Sitarek	Ćwiczenie nr: 54
rok: I	semestr: zimowy	Badanie zjawiska rezonansu elektromagnetycznego.
Wydział Elektroniki i Telekomunikacji Politechniki Wrocławskiej					Ocena:
08.03.2000 r.

1.Wiadomości wstępne.

1.1 Cel ćwiczenia.

Celem ćwiczenia jest zapoznanie ze zjawiskiem rezonansu szeregowego w obwodzie RLC, wyznaczenie częstotliwości rezonansowej i współczynników dobroci obwodów oraz zmierzenie nieznanej indukcyjności metodą rezonansową.

1.2 Wstęp teoretyczny.

Rezonansem nazywamy zjawiska szybkiego wzrostu amplitudy drgań układu fizycznego, gdy częstotliwość zewnętrznych drgań wymuszających jest zbliżona do częstotliwości drgań własnych układu - amplituda osiąga wartość maksymalną, gdy obie te częstotliwości są sobie równe.

Jednym z rodzajów rezonansu jest rezonans elektromagnetyczny występujący m.in. w szeregowym obwodzie RLC ( szeregowo połączone: opornik o oporze R, cewka o indukcyjności L i kondensator o pojemności C ) podłączonym do źródła prądu zmiennego: E(t) = E₀sin(t).

Dla takiego układu natężenie prądu będzie się zmieniać w sposób sinusoidalny, z taką samą częstotliwością, jaką wykazuje źródło prądu: I(t) = I₀sin(t+), przy czym wartości amplitudy I₀ oraz różnicy faz zależą od wielkości R, L, C, E₀ oraz w następujący sposób:

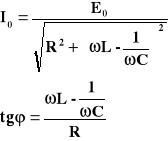
Wyrażenie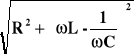
nazywamy zawadą układu RLC i stanowi ono swego rodzaju oporność tego układu. Widać wyraźnie, że przy ustalonych wartościach układu: R, L, C - amplituda I₀ osiągnie wartość największą przy najmniejszej wartości zawady, a zatem gdy: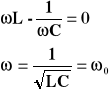
.

Wartość amplitudy jest wówczas równa:
.

Pulsacja, przy której pojawia się najwyższa wartość I₀ nazywamy pulsacją rezonansową a odpowiadającą jej częstotliwość:
nazywamy częstotliwością rezonansową.

Należy zauważyć, że wartość amplitudy natężenia prądu dla częstotliwości rezonansowej zależy tylko od oporu R, podczas gdy indukcyjność L i pojemność C mają wpływ na wartość częstotliwości rezonansowej.

Przy przechodzeniu elektronów przez opornik obserwuje się straty ich elektrycznej energii potencjalnej, która ulega przemianie w ciepło. To termodynamiczne nieodwracalne zjawisko nazywamy wydzielaniem ciepła Joule'a. Względne straty energii w obwodzie RLC są proporcjonalne do wielkości zwanej współczynnikiem dobroci układu:
.

Jedną z metod wyznaczania współczynnika dobroci jest pomiar napięcia skutecznego U_c na kondensatorze podczas rezonansu przy znajomości wartości napięcia zasilającego U_wy:
.

1.3 Układ pomiarowy.

W skład układu pomiarowego wchodzą:

• generator mocy PO-21,

• miernik napięcia przemiennego - Multimetr G 1007.500,

• miernik prądu przemiennego - V562,

• oscyloskop dwukanałowy - DT-516A,

• badany obwód RLC.

Schemat układu pomiarowego Połączenie obwodu szeregowego

dla rezonansu napięć. do oscyloskopu.

2. Przebieg ćwiczenia.

Ćwiczenie polega na zmierzeniu zależności natężenia prądu płynącego przez amperomierz od częstotliwości dla stałej wartości napięcia zasilającego obwód i na podstawie tych zależności zbadanie zjawiska rezonansu elektromagnetycznego.

Pomiary zostały wykonane dla 2 różnych rezystancji (R₁, R₃) przy stałej pojemności kondensatora C₁ = 62,53 [nF] ± 5[%], a następnie przy pojemności C₃ = 9,27 [nF] ±5 [%]. Stałe napięcie zasilające w obwodzie RLC wynosiło V=2 [V].

3. Tabele z wynikami pomiarów i obliczeń.

3.1

U_WY=2V

R1+C1					R3+C1
Lp.	f [ Hz ]	I [ mA ]	Δf [ Hz ]	ΔI [ mA ]	Lp.	f [ Hz ]	I [ mA ]	Δf [ Hz ]	ΔI [ mA ]
1.	20	0,01	0,4	0,0001	1.	20	0,01	0,4	0,0001
2.	50	0,15	1	0,0015	2.	50	0,015	1	0,00015
3.	100	0,17	2	0,0017	3.	100	0,05	2	0,0005
4.	200	0,2	4	0,002	4.	200	0,08	4	0,0008
5.	500	0,45	10	0,0045	5.	300	0,26	6	0,0026
6.	1 k	0,95	20	0,0095	6.	500	0,44	10	0,0044
7.	2 k	2,7	40	0,027	7.	1 k	0,95	20	0,0095
8.	3 k	12,8	60	0,128	8.	2 k	2,7	40	0,027
9.	3,1 k	17,8	62	0,178	9.	3 k	16,2	60	0,162
10.	3,2 k	23	63	0,23	10.	3,1 k	25,7	62	0,257
11.	3,3 k	25,3	66	0,253	11.	3,2 k	47,4	64	0,474
12.	3,4 k	21	68	0,21	12.	3,3 k	60	66	0,6
13.	3,5 k	16,2	70	0,162	13.	3,4 k	35	68	0,35
14.	3,7 k	10	74	0,1	14.	3,5 k	20	70	0,2
15.	4 k	7	80	0,07	15.	4 k	7	80	0,07
16.	5 k	3,6	100	0,036	16.	5 k	0,35	100	0,0035
17.	10 k	0,2	200	0,002	17.	10 k	0,2	200	0,002
18.	15 k	0,15	300	0,0015	18.	15 k	0,15	300	0,0015
Uc=39,3 mV					Uc=36 mV

3.2

U_WY=2V

R3+C1					R3+C3
Lp.	f [ Hz ]	I [ mA ]	Δf [ Hz ]	ΔI [ mA ]	Lp.	f [ Hz ]	I [ mA ]	Δf [ Hz ]	ΔI [ mA ]
1.	20	0,001	0,4	0,00001	1.	20	0,001	0,4	0,00001
2.	50	0,001	1	0,00001	2.	50	0,01	1	0,0001
3.	100	0,015	2	0,00015	3.	100	0,015	2	0,00015
4.	200	0,025	4	0,00025	4.	200	0,02	4	0,0002
5.	500	0,06	10	0,0006	5.	500	0,04	10	0,0004
6.	1 k	0,12	20	0,0012	6.	1 k	0,08	20	0,0008
7.	2 k	0,24	40	0,0024	7.	2 k	0,25	40	0,0025
8.	3 k	0,4	60	0,004	8.	5 k	0,45	100	0,0045
9.	4 k	0,6	80	0,006	9.	8 k	14	160	0,14
10.	5 k	0,9	100	0,009	10.	8,2 k	22	164	0,22
11.	6 k	1,4	120	0,014	11.	8,5 k	42	170	0,42
12.	7 k	2,6	140	0,026	12.	8,6 k	58	172	0,58
13.	8 k	7,6	160	0,076	13.	8,7 k	50	174	0,5
14.	8,2 k	11	164	0,11	14.	8,8 k	30	176	0,3
15.	8,3 k	16	166	0,16	15.	9 k	13,5	180	0,135
16.	8,4 k	21	168	0,21	16.	10 k	0,2	200	0,002
17.	8,5 k	28	170	0,28	17.	15 k	0,15	300	0,0015
18.	8,6 k	27	172	0,27
19.	9 k	10	180	0,1
20.	10 k	4	200	0,04
21.	15 k	0,2	300	0,002
Uc=85 mV					Uc=66,7 mV

4. Zebranie wyników:

	R1+C1	R3+C1	R3+C1	R3+C3
f0 [ Hz ]	3,3 k	3,3 k	8,7 k	8,6 k
Q	0,01965	0,018	0,0425	0,03335
ΔQ	0,05037	0,05034	0,05079	0,05063
δQ [ % ]	2,563	2,797	1,195	1,518
δL [ % ]	11,06		7,312
ΔL [ mH ]	4,045		2,68
Lśr [ mH ]	36,65

5. Obliczenie błędów pomiarów:

Δf = f⋅2%

ΔI = I⋅1%

Błąd względny
wyznaczamy metodą pochodnej logarytmicznej:

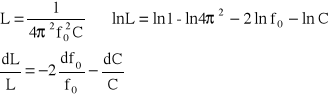
6. Przykładowe obliczenia:

ΔU = kl.⋅Zakres/100 = 0,1[V]

ΔE = 0,0375[V]

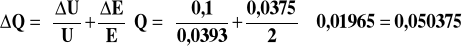
7. Wnioski:

Wykres zależności I od f₀ powinien być symetryczny względem prostej f₀f(f₀) , ale ze względu na nie stabilność napięcia zasilającego i wady generatora wykres jest niesymetryczny. W miarę malenia R wartość maksymalna funkcji dąży do nieskończoności, czyli wykres robi się bardziej stromy. Dla mniejszej pojemności C obserwuje się dłuższe dochodzenie do rezonansu.

Ponadto, jak należało się spodziewać, współczynniki dobroci mają wartość mniejszą, a zatem obserwuje się większe straty energii dla większych wartości oporów.

Pomimo teoretycznych przewidywań o równej wartości amplitudy I₀ dla równych wartości oporów, otrzymano różne wysokości krzywych rezonansowych dla odpowiednich oporów. Wydaje się to być związane z różnicami we współczynnikach dobroci - im większy współczynnik dobroci, tym większa krzywa rezonansowa.

Na podstawie uzyskanych krzywych rezonansowych możemy ustalić, że faktycznie R₁>R₃ - amplituda w czasie rezonansu ma wartość większą w przypadku R₃, a jest ona odwrotnie proporcjonalna do oporu, oraz, że prąd płynący przez obwód podczas rezonansu jest odwrotnie proporcjonalny do rezystancji. Zauważyć można również, iż częstotliwość rezonansowa zależy od pojemności kondensatora i indukcyjności cewki, a nie zależy od rezystancji, ponieważ częstotliwość ta jest odwrotnie proporcjonalna do pierwiastka z pojemności, czyli dla większej pojemności obserwuje się rezonans przy mniejszej częstotliwości.

---