Politechnika Lubelska w Lublinie	Laboratorium Ćwiczenie nr 4
Nazwisko i imię: Widz Tadeusz Wójcik Krzysztof	Semestr: II	Grupa: 2.5	Rok akademicki 96/97
Temat : Obwody nieliniowe prądu stałego.		Data wykonania. 14.03.97	Ocena:

Cel ćwiczenia: Zapoznanie się z metodami wyznaczania charakterystyk elementów nieliniowych oraz badanie obwodów nieliniowych złożonych z szeregowo i równolegle połączonych elementów nieliniowych metodami graficznymi.

Układ pomiarowy:

Tabela pomiarów:

Lp.	Element 1		Element 2		Poł. szer. 1+2		Poł. rown. 1+2
	U [ V ]	I [ A ]	U [ V ]	I [ A ]	U [ V ]	I [ A ]	U [ V ]	I [ A ]
1 2 3 4 5	5 10 15 20 25	0, 4 0, 56 0, 68 0, 78 0, 9	5 10 15 20 25	0, 66 0, 96 1, 2 1, 4 1, 6	5 10 15 20 25	0, 35 0, 5 0, 6 0, 7 0, 75	5 10 15 20 25	1, 06 1, 52 1, 88 2, 18 2, 5

Wykres 1:

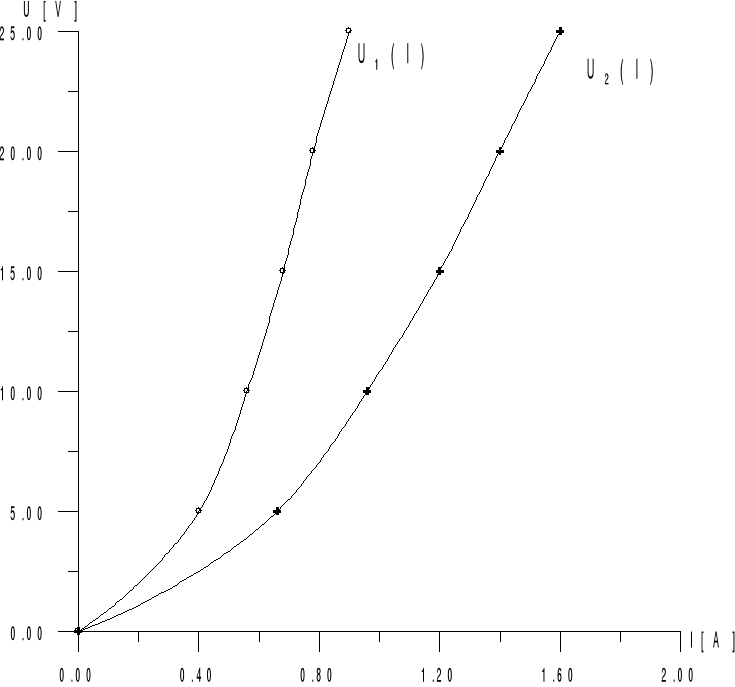
Połączenie szeregowe elementów:

Schemat pomiarowy:

Tabela pomiarowa:

Lp.	U [ V ]	I [ A ]		metoda	I [ A ]	U1 [ V ]	U2 [ V ]
1 2 3 4 5	5 10 15 20 25	0, 35 0, 5 0, 6 0, 7 0, 85		a b c	0, 75 0, 75 0, 75	18, 5 18, 5 18, 5	6, 5 6, 5 6, 5

Wykres 2:

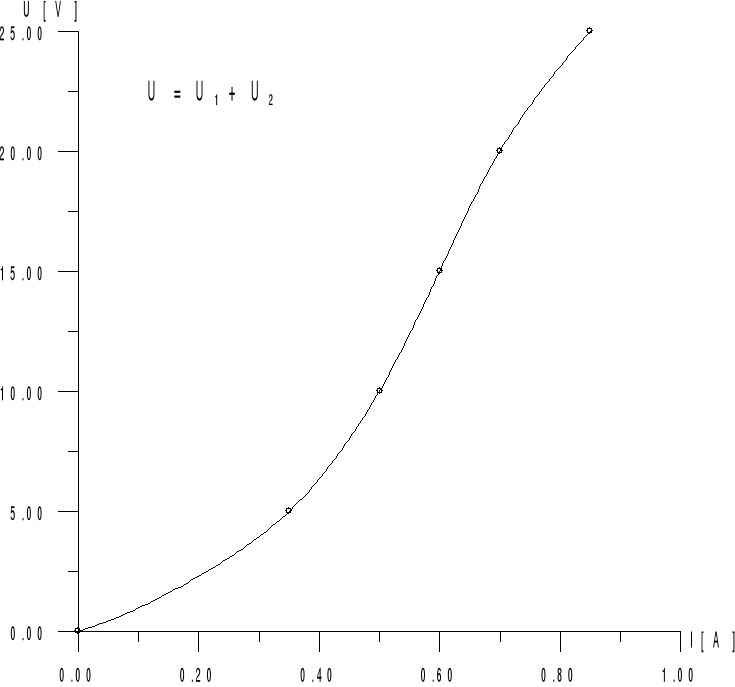
Wykres 3:

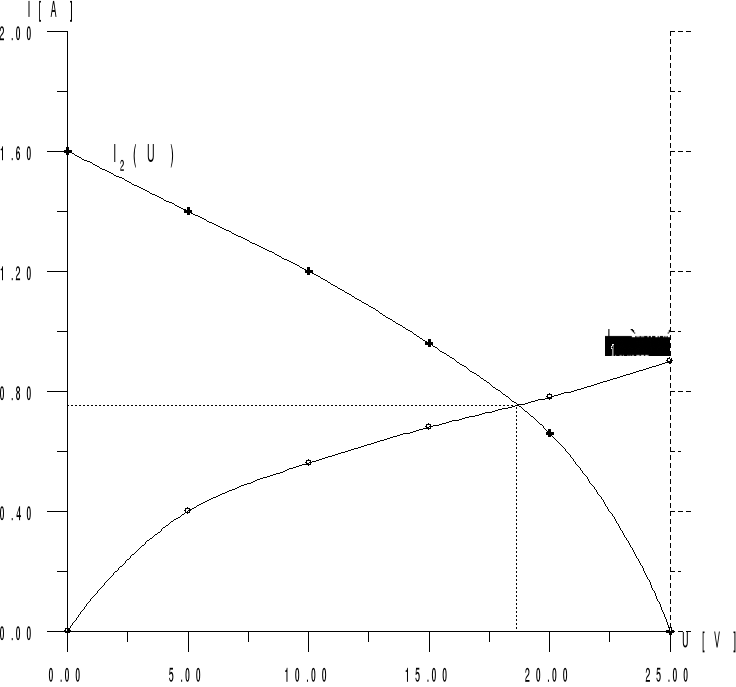
Metody

na podstawie wykresów 1 i 2

na podstawie pomiaru

na podstawie wykresu 3

Połączenie równoległe

Schemat układu

Tabela pomiarowa

Lp.	U [ V ]	I [ A ]		metoda	U [ V ]	I1 [ A ]	I2 [ A ]
1 2 3 4 5	5 10 15 20 25	1, 05 1, 5 1, 85 2, 2 2, 5		a b c	25 25 25	0, 9 0, 9 0, 9	1, 6 1, 6 1, 6

Wykres 4:

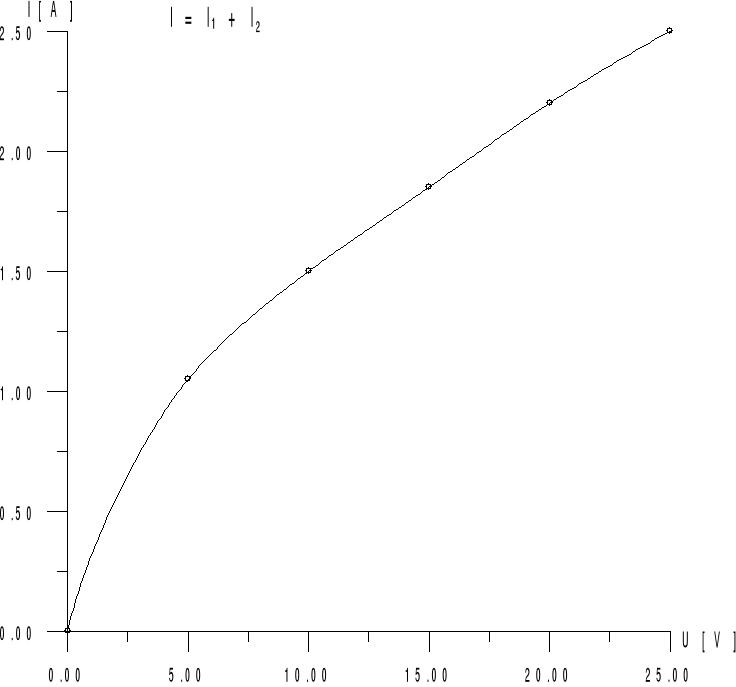
Wykres 5

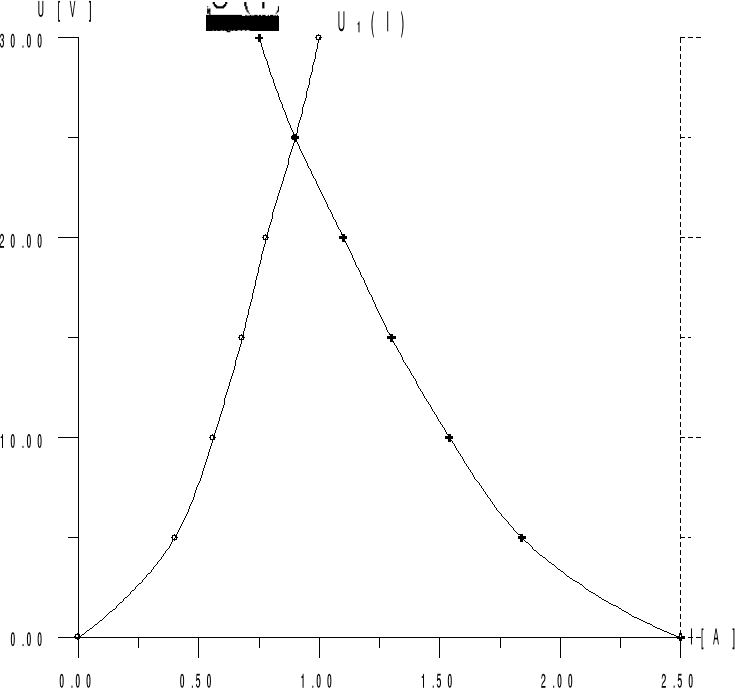
Metody:

na podstawie wykresów 1 i 4

na podstawie pomiarów

na podstawie wykresu 5

Zakres zmienności rezystancji statycznej i dynamicznej na podstawie wykonanych pomiarów:

statyczna : dla elementu 1 do 27.7 W dynamiczna: dla elementu 1 59 W

dla elementu 2 do 15.6 W dla elementu 2 29.5 W

Aproksymacja charakterystyk doświadczalnych:

Funkcja aproksymująca o postaci

Lp.	U [ V ]	logU	I [ A ]	logI
Element 1
1 2 3 4	5 10 15 20	0, 699 1 1, 176 1, 301	0, 4 0, 56 0, 68 0, 78	-0, 398 -0, 252 -0, 167 -0, 107
Element 2
1 2 3 4	5 10 15 20	0, 699 1 1, 176 1, 301	0, 66 0, 96 1, 2 1, 4	-0, 18 -0, 018 0, 079 0, 146

Wykres 6

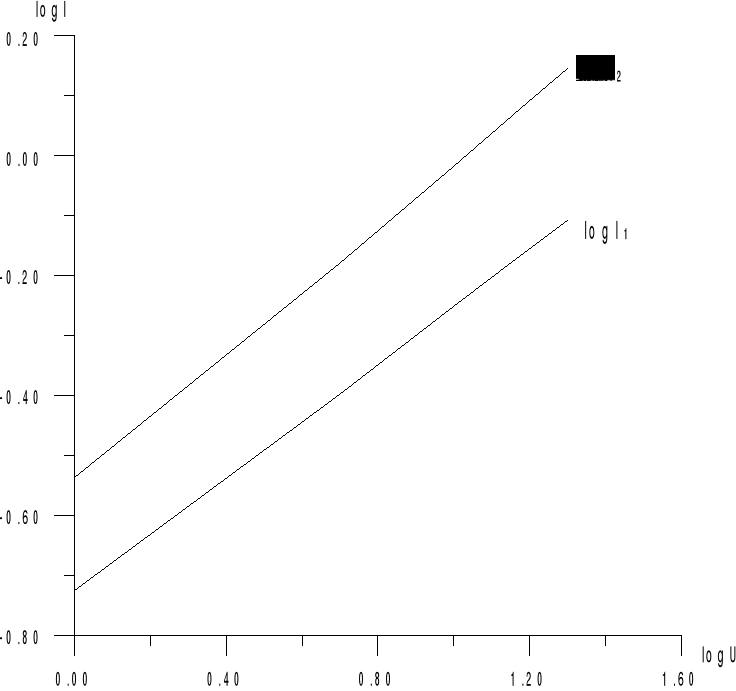
Dla elementu 1 funkcja aproksymująca charakterystykę I = f (U) ma postać

, a dla drugiego .

Wnioski:

W obwodach elektrycznych często występują elementy nieliniowe, których rezystancja zależy od przepływającego przez nie prądu. Przy dużych prądach następuje silne nagrzewanie przewodnika i związana z tym zmiana rezystancji. Obwody nieliniowe nie spełniają więc zasady superpozycji. W ćwiczeniu jako elementy nieliniowe zostały użyte żarówki z włóknem wolframowym. Mając wyznaczone doświadczalnie charakterystyki elementów można wyznaczyć charakterystyki połączeń tych elementów . W przypadku połączenia szeregowego przez rezystory płynie jednakowy prąd. Napięcia na poszczególnych elementach można wyznaczyć metodą charakterystyki łącznej U=U₁+U₂, odczytując napięcia w punktach , w których prosta równoległa do osi rzędnych i przechodząca przez punkt odpowiadający zadanemu prądowi I przecina wykresy. Jeżeli znamy napięcia na zaciskach możemy wyznaczyć prąd płynący w obwodzie i napięcie na poszczególnych elementach metodą przecięcia charakterystyk. Rysując charakterystykę elementu 1 I(U) w układzie współrzędnych, a następnie odkładając na osi odciętych punkt P. odpowiadający napięciu na zaciskach rysujemy charakterystykę drugiego elementu symetrycznie względem osi I' przechodzącej przez punkt P. Punkt przecięcia charakterystyk wyznacza nam wartość prądu płynącego w obwodzie i napięcia na poszczególnych elementach. Analogicznie wyznaczamy rozpływ prądów w gałęziach równoległych obwodów nieliniowych. Napięcie na elementach jest jednakowe, a prąd ulega rozgałęzieniu I = I₁+I₂ . Mając dane napięcie możemy wyznaczyć z charakterystyki łącznej prąd w poszczególnych gałęziach obwodu. Gdy dany jest prąd I dopływający do połączenia metodą przecięcia charakterystyk można wyznaczyć napięcie na zaciskach i prądy w poszczególnych gałęziach.

Charakterystyki wyznaczone na drodze pomiarowej można przedstawić analitycznie w postaci równania określającego zależność I (U). Aproksymacja pozwala rozwiązywać układy nieliniowe metodami analitycznymi.

---