Kogut Andrzej Rzeszów, 25-V-1996
Grupa L - 11
Sprawozdanie z laboratorium z fizyki
Ćwiczenie nr 27
1.Prąd sinusoidalnie zmienny, wielkości charakterystyczne, wielkości charakteryzujące wartość średnią, skuteczną, szczytową. Prąd elektryczny jest to zjawisko fizyczne wywołane uporządkowanym ruchem ładunków poprzez badany przekrój poprzeczny danego ośrodka. Prąd zmienny - w funkcji czasu ulega zmianie natężenie lub zwrot płynącego prądu. Prąd przemienny - zmiany te zachodzą okresowo. Prąd sinusoidalnie przemienny - prąd, którego przebieg jest sinusoidalną funkcją czasu.
i(t) = Im sin(t +)
i(t) - wartość chwilowa natężenia prądu
Im - wartość szczytowa natężenia prądu
- pulsacja (częstotliwość kołowa)
- faza początkowa
Wartość skuteczna natężenia prądu przemiennego jest to wartość
liczbowo równa takiej wielkości prądu stałego , który w tym samym
czasie i na tym samym oporze wydzieli taką samą ilość ciepła.
Wartość średnia półokresowa prądu przemiennego jest równa liczbowo takiej wartości prądu stałego , który w tym samym czasie (połowie okresu) przeniesie taki sam ładunek co dany prąd przemienny . Wartość średnia całookresowa prądu przemiennego jest równa zero , dlatego podaje się wartość średnią półokresową, liczy się ją ze wzoru.
2.
A. Indukcyjność w obwodzie prądu zmiennego .
Jeżeli do źródła prądu stałego o napięciu U przyłączymy cewkę o wielu zwojach (idealną R 0 ) to przez taką zwojnicę mógłby płynąć prąd ( teoretycznie ) o bardzo dużym natężeniu ograniczonym tylko opornością wewnętrzną źródła .Jeżeli tę samą cewkę ( pozbawioną oporności czynnej ) przyłączymy do źródła prądu zmiennego to natężenie prądu będzie ograniczone poprzez siłę elektromotoryczną indukcji własnej
eL = - L (di/dt) lub eL = -z (d/dt)
L- współczynnik indukcyjności własnej
- szybkość zmian strumienia
Gdy L > 0 , R=0 , C=0
i = Imsin(t)
spadek napięcia uL= -eL
Jak widać natężenie prądu jest opóźnione o kąt 900 w stosunku do napięcia .
B. Kondensator w obwodzie prądu zmiennego.
Napięcie doprowadzone ze źródła prądu zmiennego do okładzin kondensatora zmienia się sinusoidalnie :
u = Umsin(t)
jak i prąd w kondensatorze
i = dq/dt
dq = Cdu= CUm cos(t)dt
i = CUmcos(t)
cos = sin (+/2)
i = CUmsin (t+/2)
Przepływający przez kondensator prąd zmienny ma natężenie o prze-
biegu sinusoidalnym , które wyprzedza napięcie o kąt 900 .
Szczytowa wartość natężenia prądu wynosi : Im = CUm
C. Rezystor w obwodzie prądu zmiennego.
R > 0, L = 0, C = 0
Wartość natężenia prądu przepływającego przez opornik wyraża się równaniem i =Imsin(t)
Spadek napięcia na oporności czynnej R przy jej niezmiennej
wartości jest wprost proporcjonalny do natężenia przepływającego prądu. Chwilowe napięcie jest największe ( Um ) gdy wartość chwilowa przepływającego prądu jest największa . Napięcie i prąd są zgodne w fazie. Związek między napięciem i prądem chwilowym U = RImsin(t) .
D. Obwód szeregowy RLC
Obwód szeregowy RLC składa się z połączonych ze sobą szeregowo rezystancji, indukcyjności i pojemności. Napięcie chwilowe u = uR +uL + uC.
Wartość skuteczna napięcia doprowadzonego do zacisków układu jest sumą geometryczną uR , u L ,u C .UL i uC są przesunięte w fazie względem uR o +90 i -90 .
![]()
![]()
Z - impedancja (oporność pozorna )
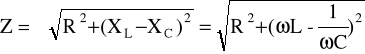
Obwody zasilane prądem zmiennym, zawierające elementy bierne i czynne powodują przesunięcie fazowe pomiędzy prądem a napięciem. Kąt przesunięcia fazowego jest określony poprzez
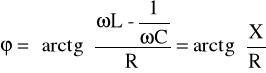
3.
Wykonanie ćwiczenia:
1. Połączenie obwodu wg. schematu:
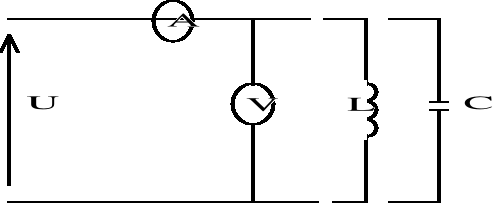
1.a) Przyrządy do wykonania ćwiczenia:
Amperomierz i voltomierz na prąd stały i przemienny, kondensator, cewka.
2. Wyznaczam opór czynny z prawa Ohma (dla prądu stałego)
![]()
Tabela pomiarowa dla wyznaczenia oporu czynnego z prawa Ohma (dla prądu stałego)
Lp |
U [V] |
I [A] |
R [] |
1 |
2,5 |
0,13 |
19,23 |
2 |
5 |
0,26 |
19,23 |
3 |
7,5 |
0,395 |
18,98 |
4 |
10 |
0,53 |
18,86 |
5 |
11 |
0,58 |
18,95 |
6 |
12,5 |
0,66 |
19,69 |
R i R wyznaczone graficznie na załączonym wykresie
R = ctg ; R=20
R = 1.4
3. Wyznaczam oporność pozorną cewki (prąd zmienny)
![]()
Tabela pomiarowa dla wyznaczenia oporności pozornej cewki:
Lp |
U [V] |
I [A] |
Z [] |
1 |
10 |
0,23 |
43,47 |
2 |
15 |
0,34 |
44,11 |
3 |
20 |
0,47 |
42,55 |
4 |
25 |
0,57 |
43,85 |
5 |
30 |
0,7 |
42,85 |
6 |
35 |
0,79 |
44,30 |
Z oraz Z również wyznaczone graficznie na załączonym wykresie
Z = ctg ; Z = 22.7
Z = 0.3
4. Obliczam indukcyjność cewki:
![]()
f = 50 Hz.
L = 3067.8H
L obliczam z różniczki zupełnej:
L = 0,2376 H
![]()
=0.2376
5. Wymieniam cewkę na kondensator i wyznaczam oporność bierną kondensatora przy zasilaaniu prądem zmiennym:
![]()
Tabela pomiarowa:
Lp |
U [V] |
I [A] |
XC[] |
1 |
34 |
0,1 |
340 |
2 |
48 |
0,15 |
320 |
3 |
63 |
0,2 |
315 |
4 |
78 |
0,25 |
312 |
5 |
84 |
0,27 |
311,11 |
6 |
94 |
0,3 |
313,33 |
XC oraz XC wyliczam korzystając z metody najmniejszych kwadratów.
XC = 318
6. Oblczam wartość pojemności z zależności:
![]()
C = 0,00001 F
Błąd C oblczam z różniczki zupełnej.
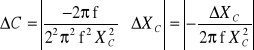
Wnioski:
Na podstawie przeprowadzonych pomiarów i obliczeń wnioskuję, że doświadczenie przebiegło pomyślnie. Zaistniałe błędy mogły wyniknąć "z przyczyn niezależnych" tzn. niestabilne napięcie zasilające, niestała częstotliwość prądu w sieci elektrycznej a także niedokładność pomiarów na miernikach. Na błędy pomiarowe złożyły się następujące czynniki: nieprecyzyjny odczyt ze skali wskazówkowej, błędy sprzętowe, niestabilność układu zasilającego. Pomimo zaistniałych błędów wyniki uzyskane przy pomiarach jak i w późniejszych obliczeniach uważam za zadowalające.
Wyszukiwarka
Podobne podstrony:
27 PUSTE, Kogut Andrzej_______ Rzesz?w, 25-V-1996
L10, Kogut Andrzej Rzesz˙w, 25-V-1996
10, Kogut Andrzej_________Rzesz?w 16-05-96
51, Kogut Andrzej Rzesz˙w 25-05-96
CW10, Kogut Andrzej Rzesz˙w 16-05-96
1996 06 25 1147
Lab fiz 09, Piotr Mazur Rzesz˙w 27.02.1996
01 1996 24 25
05 1996 25
CW47, Marcin Kwoka
CW1, Marcin Kwoka
CW9, Piotr Mazur Rzesz˙w 27.02.1996
Ruch obrotowy bryly = 2, Piotr Mazur______ Rzesz?w 27.02.1996
1996 06 25 1140
04 1996 25
AKS-ŹW1, Piotr Mazur Rzesz˙w 27.02.1996
AKS-ŹW8, Piotr Mazur Rzesz˙w 27.02.1996
Ruch obrotowy bryly = , Piotr Mazur______ Rzesz?w 27.02.1996
07 1996 25 26
więcej podobnych podstron