[28] Przemieszczenie ciała sztywnego z jednym unieruchomionym punktem

Łatwo można zauważyć, że podobnie jak to było w przypadku ruchu płaskiego, gdzie mógł on być sprowadzony do ruchu jedynie obrotowego względem środka obrotu, również w przypadku ruchu kulistego dowolne przemieszczenie ciała sztywnego może być zrealizowane poprzez obrót wokół osi przechodzącej przez punkt nieruchomy ciała 0. Na rys. 6.8 pokazano, w jaki sposób wyznaczyć wspomnianą oś.

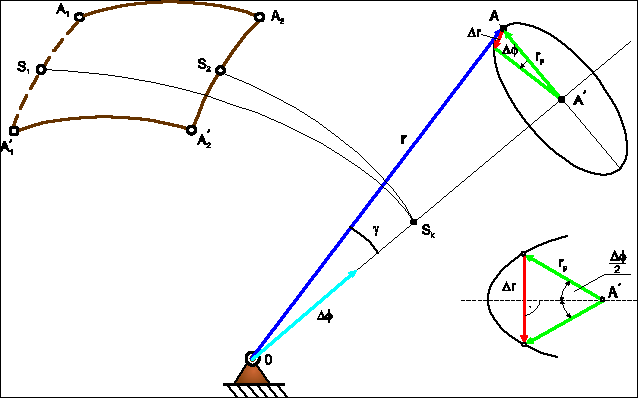
Rys. 6.8. Konstrukcja osi obrotu ciała sztywnego wykonującego ruch kulisty (A₁A₂=A₁^'A₂^')

Niech odcinek A₁A₂ leżący na sferze o promieniu 0A₁ w chwili czasu t₀ znajdzie się w położeniu
w chwili czasu t₁. W celu wyznaczenia drugiego punktu należącego do poszukiwanej osi obrotu wyznaczamy środki łuków
i
, a następnie przez te środki S₁ i S₂ prowadzimy prostopadłe łuki należące do okręgów wielkich kul, które przetną się w poszukiwanym punkcie S_k. Można wykazać, że trójkąt A₁S_kA₂ pokryje się z trójkątem
po obrocie wokół osi 0S_k o pewien kąt φ. Oś 0S_k będziemy nazywać chwilową osią obrotu ciała sztywnego. Mając wyznaczoną chwilową oś obrotu łatwo określimy przemieszczenie dowolnego punktu A. Prowadząc z tego punktu prostopadłą do tej osi otrzymamy punkt
, i wobec tego punkt A podczas ruchu kulistego ciała sztywnego będzie się poruszał po okręgu o promieniu
Małe przemieszczenie Δr punktu A wynosi (patrz rys. 6.8)

(6.69)

Zauważmy, że

(6.70)

Pokażemy, że kolejne małe obroty ciała sztywnego mogą być zastąpione jednym małym obrotem wypadkowym tego ciała. W rozważaniach ograniczymy się do dwóch obrotów.

Po pierwszy obrocie punkt A znajdzie się w położeniu określonym promieniem wektorem

(6.71)

Po drugim obrocie punkt A znajdzie się w położeniu określonym promieniem wektorem

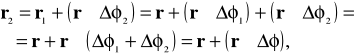
(6.72)

gdzie

(6.73)

---