Wanat Karol

I ED

Ćwiczenie nr 43

Wyznaczanie zdolności pochłaniania światła przez szkło o zmiennej grubości i sprawdzanie graficzne pochłaniania światła.

Zagadnienia do samodzielnego opracowania

1. Fotometr - zasada działania

2. Prawo pochłaniania światła przez ośrodki przeźroczyste

3. Jednostki fotometryczne

I. Wprowadzenie

Fotometria jest działem fizyki zajmującym się pomiarami promieniowania. Poniżej zdefiniowane wielkości fotometryczne używane są w przypadku fotometrii w zakresie widzialnych fal elektromagnetycznych.

Całkowitą ilość energii, wysyłaną przez źródło światła we wszystkich kierunkach w ciągu 1 sekundy nazywamy strumieniem energii. Natomiast strumień świetlny Φ jest to moc promieniowania oceniona na podstawie wywoływanego przez nią wrażenia wzrokowego w oku.

Jednostką strumienia świetlnego jest lumen [ lm ] zdefiniowany jako strumień świetlny punktowego źródła światła o natężeniu 1 kandeli w obrębie kąta bryłowego 1 steradianu [ sr ].

Natężeniem światła I wysyłanego w nieskończone mały kąt bryłowy dΩ jest stosunek strumienia świetlnego dΦ zawartego w granicach tego kąta bryłowego do niego wartości

Jeżeli źródło promieniuje we wszystkich kierunkach jednakowo silnie ( jest izotopowe) wówczas
. Międzynarodową jednostką natężenia światła jest kandela [ cd ], zdefiniowana przez natężenie światła wysyłanego przez powierzchnię
ciała doskonale czarnego w temperaturze 1773^oC w kierunku prostopadłym do powierzchni.

Oświetleniem powierzchni nazywamy wielkość:

gdzie dS jest elementem powierzchni prostopadłym do strumienia świetlnego.

Jednostką oświetlenia jest luks [ lx ] zdefiniowany jako oświetlenie powodowane przez strumień 1 lumena padający prostopadle na powierzchnię 1 m².

Oświetlenie dowolnej powierzchni znajdującej się w odległości r od źródła punktowego o natężeniu I i nachylonej pod kątem φ do kierunku padania światła wyraża się wzorem:

lub po przekształceniu
.

II. Zasada pomiaru.

Z doświadczenia wiadomo, że w miarę rozchodzenia się fali świetlnej w materii, jej natężenie stopniowo maleje. Zjawisko to nazywa się pochłanianiem światła w materii ( absorbcją światła ).

Zmniejszenie natężenia -dI przy przejściu przez warstwę o grubości dx jest proporcjonalne do wartości natężenia światła oraz do grubości warstwy dx:

gdzie μ jest współczynnikiem proporcjonalności nazywanym współczynnikiem pochłaniania danej warstwy. Jeżeli światło przechodzi przez warstwę o grubości x i zmienia się od wartości początkowej I (0) do wartości końcowej I (x), to po scałkowaniu w tych granicach

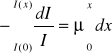
otrzymujemy:

Sens fizyczny współczynnika pochłaniania łatwo zauważyć przekształcając ostatnie równanie postaci:

A zatem współczynnik pochłaniania μ jest liczbowo równy jedności podzielonej przez grubość warstwy substancji x = a, po przejściu której natężenie światła maleje e ≈ 2,72 razy.

Zdolność pochłaniania ( absorbcji ) A(x) określona jest jako względna wartość natężenia światła pochłoniętego przez dany ośrodek o grubości x:

podobnie, I - A(x) określa przepuszczalność danego ośrodka.

III. Wykonanie ćwiczenia

Przyrządy: ława optyczna, dwa źródła światła, fotometr, płytki szklane, uchwyt do płytek,

śruba mikrometryczna.

1. Starannie oczyściłem kilkanaście płytek szklanych. Zmierzyłem grubość każdej z nich śrubą mikrometryczną. Odliczyłem średnią wartość grubości płytki d_S.

2. Na ławie optycznej ustawiłem dwa jednakowe źródła światła w położeniu, tak aby oświetlenie obu połówek było jednakowe. Wówczas I(r) = I(0), gdzie r oznacza odległość źródeł światła od obu powierzchni fotometru.

3. Do uchwytu wstawiłem warstwę składającą się z trzech płytek szklanych między źródłem Z₁ a fotometrem (grubość warstwy pochłaniającej x₁ = 3d_S). Doprowadziłem do zrównania oświetlenia obu pól kostki fotometrycznej. Zmierzyłem odległość r₁(x₁), r₁(x₁) fotometru od źródeł odpowiednio Z₁ i Z₂. Ponieważ oświetlenie obu powierzchni fotometru jest jednakowe to
   . Wartość natężenia światła po przejściu przez warstwę trzech płytek o grubości x₁ zmniejszyła się od I(0) do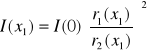
   .

4. Podobnie jak w punkcie trzecim wykonałem pomiary natężenia światła po przejściu przez warstwy płytek o grubościach x₂, x₃,... = 6d_S, 9d_S,... .

5. Na papierze milimetrowym sporządziłem wykres zależności I(x). Na podstawie tego wykresu oszacowałem wartość współczynnika pochłaniania μ. Odczytałam z wykresu wartość x = a, dla której
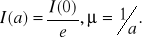
   Na wykresie uwzględniłem błędy pomiarowe.

6. Postępowanie opisane w punkcie 5. dotyczące wyznaczania μ nie pozwala jednoznacznie określić jego wartości i błędu pomiaru. Zauważyłem, że
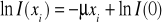
   przedstawia linię prostą o współczynniku nachylenia -μ i w punkcie przecięcia z osią rzędnych ln I(0). Korzystając z metody najmniejszych kwadratów, zbioru wyników pomiaru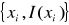
   możemy wyznaczyć najbardziej prawdopodobną wartość współczynnika pochłaniania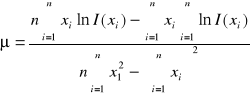
   oraz ocenić dokładność przeprowadzanego pomiaru obliczając współczynnik korelacji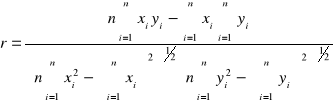
   gdzie y_i = ln I(x_i) i n oznacza liczbę pomiarów.

7. Oceniłem błędy pomiarów.

8. Wyniki umieściłem w tabelce.

Lp.	I(0)	dS	xi	r1(xi)	r2(xi)	Δr	I(xi)	ΔI	A(xi)	μ
—	[ k ]	[ cm ]	[ mm ]	[ cm ]	[ cm ]	[ cm ]	[ cd ]	[ cd ]	[ ]	[mm^-1]
1. 2. 3. 4.	19 19 19 19	7,66 17,46 39,78 50,52	7,18 14,71 22,04 29,69	51,5 55 61,5 62,5	48,5 45 38,5 37,5	3,8	16,85 12,72 7,44 6,84	±5,05 ±3,94 ±2,35 ±2,24	0,11 0,33 0,61 0,64	0,902

---