Drgania

• Wykres wychylenia od czasu, prędkości od czasu i przyspieszenia od czasu dla drgań harmonicznych.

• Wahadło matematyczne- okres drgań, siły działające na wahadło

• Ciało zawieszone na sprężynie - okres drgań

• Przemiany energii w ruchu drgającym

• zjawisko rezonansu mechanicznego i jego przykłady

1. Oblicz długość wahadła matematycznego o okresie T = 2 s. Ile będzie wynosił okres drgań wahadła jeżeli zwiększymy jego masę 4-ro krotnie.

2. Okres drgań wahadła matematycznego o długości 0,6 m na planecie X wynosi T = 0,983 s. Oblicz przyspieszenie grawitacyjne na powierzchni tej planety. Ile razy jest ono większe od przyspieszenia ziemskiego?

3. Dwa wahadła matematyczne zostały wprawione w ruch wahadłowy w tej samej chwili i po upływie pewnego czasu jedno z nich wykonało 3 wahnięcia, a drugie 5 wahnięć. Na jak długiej nici zawieszone jest każde z wahadeł, jeśli różnica długości tych nici 32 cm?

4. W windzie zawieszono wahadełko, którego okres drgań wynosi T = 0,3 s. Z jaką częstotliwością będzie się ono wahać, gdy winda będzie się poruszała z przyspieszeniem a = ng (gdzie n = 0,91) skierowanym do dołu?

5. Wy
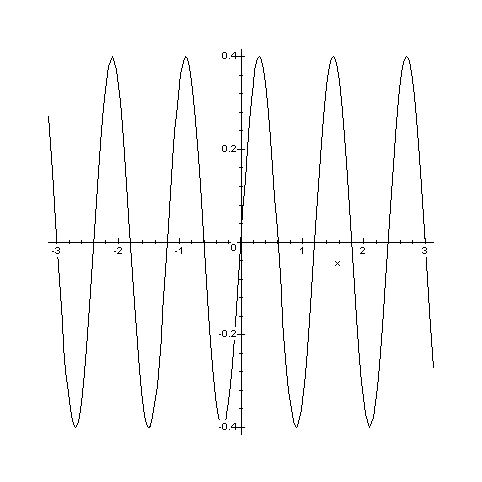
   kres położenia ciała w ruchu drgającym przedstawia rysunek. Odczytaj z wykresu: a) ile wynosi amplituda drgań? b) jakie jest wychylenie w chwili t = 0,9 s? c) ile wynosi okres drgań? Oblicz: a) jakie jest wychylenie w chwili t = 0,3 s, b) częstotliwość drgań, c) prędkość w chwili t = 0 s i t = 1 s, d) maksymalną wartość prędkości, e) energię drgań, jeżeli masa ciała wynosi 0,5 kg.

6. Oblicz maksymalną prędkość i energię drgań kulki o masie 0,1 kg, gdy amplituda jej drgań jest równa 0,2 m, a częstotliwość wynosi 15 Hz.

7. Oblicz maksymalną prędkość kulki wahadła, którego długość l = 0,6 m, jeżeli jego amplituda drgań wynosi 0,1 m.

8. Na sprężynie o współczynniku sprężystości 2N/ cm zawieszono obciążnik o masie 0,04 kg. Aby wprawić układ w ruch wydłużono sprężynę dodatkowo o 2 cm, a następnie puszczono. W chwili przechodzenia układu przez położenie równowagi rozpoczęto pomiar czasu. Oblicz okres drgań tego układu. b) Wykonaj wykres siły harmonicznej od czasu

9. Klocek o małej masie przyczepiony do sprężyny wykonuje drgania harmoniczne . Maksymalna energia potencjalna układu wynosi 60J. Oblicz energie kinetyczna w chwili, w której wychylenie jest równe połowie amplitudy.

10. Klocek ma masę 0,1 kg, a współczynnik sprężystości sprężyny wynosi 10 N/cm.

oblicz wartość przyspieszenia drgającego klocka, w chwili gdy jest wychylony o 5cm.

b) oblicz okres drgań tego klocka, gdy zostanie wychylony z położenia równowagi. Jak zmieni się okres drgań jeżeli masa klocka wzrośnie 4-ro krotnie.

1. Oblicz całkowitą energię mechaniczną drgań oscylatora harmonicznego o masie m = 1 g wykonującego drgania o częstotliwości f = 300 Hz i amplitudzie A = 6 mm.

2. Wyjaśnij pojęcie rezonansu mechanicznego i podaj przykłady jego prezentacji.

3. Wiszący na sprężynie ciężarek o masie 60g wykonuje drgania harmoniczne o okresie 2 s z amplitudą 2 cm.

a) Narysuj wykres zależności wychylenia drgającego ciężarka od czasu.

b) Oblicz prędkość maksymalną ciężarka.

c) oblicz maksymalną energię potencjalna sprężystości

---