[13] Ruch krzywoliniowy

Oprócz opisanych ruchów jednostajnie przyspieszonych i jednostajnie opóźnionych ruch punktu po prostej może być ruchem harmonicznym. Jak zobaczymy później, ruch taki może również może być opisany takim samym równaniem, gdy torem punktu jest okrąg.

Ruch ten opisuje następujące równanie różniczkowe rzędu drugiego

, (2.10)

którego rozwiązaniem jest

. (2.11)

W powyższym równaniu a oznacza amplitudę ruchu, α oznacza częstość lub pulsację ruchu punktu, a kąt θ₀ nazywany jest fazą początkową, bowiem argument
nazywany jest fazą ruchu harmonicznego. Amplituda ruchu oraz faza początkowa jest określona poprzez nadanie warunków początkowych ruchu (z matematycznego punktu widzenia jest to zagadnienie Cauchy'ego). Analizę ruchu przeprowadzimy w oparciu o równanie (2.11). Łatwo zauważyć, że ruch odbywa się wokół punktu 0, który jest początkiem przyjętej osi liczbowej. Maksymalne oddalenie punktu od początku osi 0 wynosi a, czyli jest równe amplitudzie ruchu. Ponieważ ruch jest harmonicznym, to spróbujmy wyznaczyć najmniejszy czas T po którym ruch zacznie się powtarzać. Warunek powtarzalności przyjmie postać

, (2.12)

skąd znajdujemy
. Z ostatniego równania określimy częstotliwość ruchu jako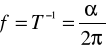
, (2.13)

rozumianą jako liczba okresów przypadającą na jednostkę czasu. Różniczkując równanie (2.11) łatwo wyznaczymy prędkość i przyspieszenie ruchu punktu

,
. (2.14)

Zauważmy, że w chwilach dla których prędkość jest równa zero, przyspieszenie osiąga wartość maksymalną. Prostą interpretację ruchu harmonicznego można otrzymać analizując ruch punktu po okręgu. Z rys. 2.4 wynika, że rzutując punkt poruszający się po okręgu na oś 0x otrzymujemy

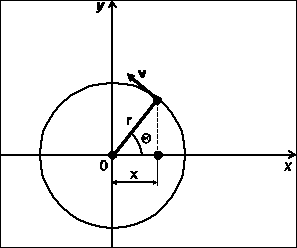
Rys 2.4. Ruch punktu po okręgu ze stałą prędkością
.

, (2.15)

czyli, że jest to ruch harmoniczny.

Ruch krzywoliniowy po okręgu jest szczególnym przypadkiem ruchu punktu po elipsie.

---