BŁĘDY POMIARU

X - wynik pomiaru

X_rz - wartość rzeczywista wielkości mierzonej

Błąd bezwzględny pomiaru: _rz = X - X_rz

Błąd względny pomiaru: δ_rz    X_rz

Ze względów praktycznych wartość rzeczywistą zastępuje się wartością poprawną, X_p , bardzo bliską wartości rzeczywistej.

Wówczas błąd bezwzględny: _p = X - X_p

i błąd względny δ_p    X_p

Przykład. Jaki jest błąd zaokrąglenia liczy π do wartości 3,142 ?

Za wartość poprawną liczby π można przyjąć liczbę 3,141593. Zatem błąd bezwzględny zaokrąglenia wynosi _p = 3,142-3,141593=0,000407, błąd względny wynosi δ_p  ,,  ,

BŁĄD GRANICZNY

• największa z możliwych wartości błędów,

• przedział wokół wyniku pomiaru, w którym mieści się wartość rzeczywista,

• taka wartość, która spełnia nierówność:

ΔX ≥ X - X_rz 

Rozwiązaniem tej nierówności jest:

X - ΔX ≤ X_rz ≤ X + ΔX

Dla podkreślenia tego, że błąd jest błędem granicznym zapisuje się ±ΔX.

Symboliczny zapis wyniku pomiaru : X ±ΔX

Ze względów praktycznych do obliczenia błędów względnych wartość rzeczywistą zastępuje się wartością zmierzoną. Wówczas błąd względny wynosi:

δX  X  X

Przyczyny występowania błędów:

• niedoskonałość narzędzi pomiarowych,

• metoda pomiarowa - uproszczenia metody, czułość układu itp.,

• uproszczone charakterystyki przetwarzania, np. nieliniowość,

• uproszczone obliczenia,

• uproszczenie modelu wielkości mierzonej,

• wpływ otoczenia ( warunków zewnętrznych )

• subiektywny odczyt z pola analogowego.

Ze względu na różne źródła i przyczyny można wyróżnić błędy:

• narzędzi pomiarowych

• metody,

• obliczeń

• uproszczeń modelowych

• wpływu warunków

• zewnętrznych

• odczytu.

Niektóre z wymienionych błędów charakteryzują się tym, że przy wielokrotnym powtarzaniu pomiaru w tych samych warunkach nie zmieniają się, inne mimo zachowania tych samych warunków, przy powtarzaniu pomiarów zmieniają wartości w sposób losowy.

Pierwsze - to błędy systematyczne, drugie - przypadkowe.

Błędy systematyczne

Są to błędy, które przy wielu pomiarach tej samej wielkości mierzonej, wykonywanych w tych samych warunkach, pozostają stałe lub zmieniają się według określonego prawa wraz ze zmianą warunków odniesienia.

Źródła i przyczyny błędów systematycznych :

1.Oddziaływanie przyrządu na obiekt mierzony - naruszenie równowagi energetycznej obiektu - błąd metody

przykłady: - pomiar temperatury termometrem kontaktowym

- pomiar napięcia woltomierzem, zmieniamy rozpływ prądu

- pomiar prądu amperomierzem, zwiększamy rezystancję obwodu.

2. Niedokładność miary wzorca, błąd wzorcowania przyrządu

błąd wzorcowania

przykłady : - uproszczenie modelu, konstrukcji, założenie liniowości podziałki, niedoskonałość wykonania,

3. Zmiany warunków pomiaru w stosunku do przyjętych warunków odniesienia - błąd dodatkowy

przykład : zmiana rezystancji rezystorów wraz ze zmianą temperatury

poprawka - błąd systematyczny z przeciwnym znakiem: P = - 

Ostatecznie wynik pomiaru: X + P ± X

Błędy przypadkowe

Są to błędy, które zmieniają się w sposób nieprzewidziany w niezmienionych warunkach pomiarów.

źródła i przyczyny:

- błędy odczytu wskazań z przyrządu analogowego,

- histereza wskazań,

- szumy termiczne

- nieuwaga obserwatora

- krótkotrwałe zmiany warunków zewnętrznych niezauważone przez obserwatora

Właściwości błędów przypadkowych :

- błędy są zdarzeniami niezależnymi

- błędy o małych wartościach zdarzają się częściej niż duże

- błędy o jednakowych wartościach i przeciwnych znakach są jednakowo prawdopodobne

- prawdopodobieństwo wystąpienia błędu przekraczającego pewną liczbę jest bardzo małe

Powyższe właściwości pozwalają przyjąć, że wyniki pomiarów obarczone błędami przypadkowymi lub same błędy przypadkowe można uważać za

zmienną losową o rozkładzie normalnym.

Rozkład normalny

Funkcja gęstości rozkładu normalnego dla wyników pomiarów:

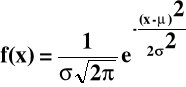
gdzie: x - wynik pomiaru, μ- wartość rzeczywista,

σ² - wariancja, σ - odchylenie standardowe.

Przebieg gęstości prawdopodobieństwa rozkładu normalnego:

Właściwości rozkładu:

w punkcie x = μ funkcja f(x) ma maksimum, jest symetryczna względem tego punktu i jej wartość zależy tylko od wartości σ.

Prawdopodobieństwo tego, że wynik x przyjmie wartości z przedziału ( x₁ , x₂ ) wynosi:

P (x₁ < x < x₂ ) =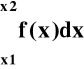

Wartość μ nie jest znana, ale najbardziej prawdopodobną wartością rzeczywistą jest średnia arytmetyczna z serii jednakowo dokładnych wyników: μ ∼x .Wówczas prawdopodobieństwo, że wartość rzeczywista będzie w przedziałach wynosi:

P ( x - σ < μ < x + σ ) = 0,68

P ( x - 2σ < μ < x + 2σ ) = 0,95

P ( x - 3σ < μ < x + 3σ ) = 0,997

Tym samym prawdopodobieństwo, że wartość błędu rzeczywistego nie przekracza wartości kσ wynosi :

P ( X < σ ) = 0,68

P ( X < 2σ ) = 0,95

P ( X < 3σ ) = 0,997

Prawdopodobieństwo równe 0,997 jest tak duże , że w praktyce pomiarowej przyjmuje się za wartość w przybliżeniu 1. Stąd wartość błądu granicznego przypadkowego pojedynczego wyniku wynosi:

X = 3σ

Obliczanie błędów przypadkowych

x₁, x₂, x₃,.....x_n - seria n pomiarów tej samej wartości,

liczba n jest duża ( n > 25 )

Wartością najbardziej prawdopodobną wielkości mierzonej jest wartość średnia :

x =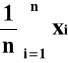
,

oszacowaniem rozrzutu wyników jest odchylenie średnie kwadratowe :

s =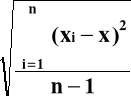

błąd graniczny przypadkowy pojedynczego wyniku

ΔX = 2s ( dla P = 0,95)

ΔX = 3s ( dla P = 0,997)

Jeśli za wynik pomiaru uznamy wartość średnią , to jej błąd graniczny przypadkowy jest mniejszy i wynosi:

ΔX = 2s /
( dla P = 0,95)

ΔX = 3s /
( dla P = 0,997)

Ogólnie : graniczny błąd przypadkowy jest kilka razy większy od odchylenia standardowego. A ile razy, to zależy od prawdopodobieństwa P oraz liczby n pomiarów w oparciu o które wykonujemy obliczenia. Dla mniejszej liczby pomiarów korzystamy z rozkładu t- Studenta, z którego obliczamy współczynnik t np przez który należy pomnożyć odchylenie standardowe, aby obliczyć graniczny błąd przypadkowy - tzw. niepewność pomiaru.

X = t np *s

tnp - współczynniki rozkładu t - Studenta

n P = 0,95 P = 0,997

5 2,8 6,6

7 2,7 4,5

10 2,3 4,1

20 2,1 3,4

30 2,0 3,3

Ogólnie:

wynikiem pomiaru jest wartość średnia i jej niepewność :

x ± t np *s /

---