36. PRZEDSTAWIĆ WYRÓWNANIE SIECI GEODEZYJNEJ METODĄ POŚREDNICZĄCĄ NA PRZYKŁADZIE SIECI NIWELACYJNEJ.

POJĘCIA:

sieć geodezyjna - sieć punktów geodezyjnych, których położenie (sytuacyjne - sieci poziome, wysokościowe - sieci niwelacyjne) określone zostało przy użyciu metod geodezyjnych, jednorodnych

wyrównanie wyników pomiarów - wyznaczenie estymatora wartości prawdziwej mierzonej wielkości; w przypadku, gdy odchylenie standardowe, określające dokładność pomiaru nie jest znane, należy również wyznaczyć estymator tego parametru (m₀)

estymator - statystyczne oszacowanie rozważanej wielkości, funkcja wyników obserwacji

METODA POŚREDNICZĄCA (PARAMETRYCZNA)

Charakteryzuje się tym, że zawsze występują niewiadome pośredniczące.

/ oprócz m. pośredniczącej poznaliśmy jeszcze m. zawarunkowaną /

Interesujące nas wielkości nie podlegają bezpośrednio pomiarom, możemy natomiast mierzyć funkcje tych wielkości.

Równanie obserwacyjne przyjmuje postać:

Li = F (x₁, x₂, …, x_n) + ε_i .

Należy dobrać takie estymatory (wartości wyrównane)

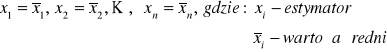
aby spełniona była funkcja celu.

Przy estymacji metodą najmniejszych kwadratów funkcja celu ma postać:

a) Σv_i² = min (obserwacje jednakowodokładne)

b) Σp_i·v_i² = min (obserwacje niejednakowodokładne)

v_i = - ε_i

W procesie wyrównania wykorzystuje się:

(1) model funkcjonalny - określa zależności funkcyjne między obserwacjami i wyznaczanymi parametrami; jest definowany przez układ równań obserwacyjnych,

V = AX - L ;

(2) model stochastyczny - to oszacowana macierz wariancyjno - kowariancyjna wektora obserwacji określająca dokładność obserwacji oraz istniejące między nimi korelacje,

C_L = σ₀² P^-1 .

WYRÓWNANIE SIECI NIWELACYJNEJ METODĄ POŚREDNICZĄCĄ

opiera się na wynikach pomiaru przewyższeń przy wyznaczaniu wysokości punktów

Etapy wyrównania (algorytm):

1. Budujemy model funkcjonalny - tworzymy układ równań obserwacyjnych:

L_i + v_i = F (x₁, x₂, …, x_k), i = 1, 2, …, n

gdzie: n - ilość obserwacji

k - ilość niewiadomych pośredniczących

i zapisujemy go w postaci macierzowej:

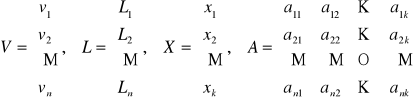
V = AX - L

gdzie: V - wektor poprawek

L - wektor wyrazów wolnych

X - wektor niewiadomych pośredniczących

A - macierz parametrów ??? (jak ktoś dotrze, jak się nazywa ta macierz, to niechby dał znać, też chcemy wiedzieć)

2. Tworzymy model stochastyczny - szacujemy macierz wariancyjno - kowariancyjną wektora obserwacji (tworzymy macierz wagową)

Dla każdego równania obserwacyjnego definiujemy wagę:

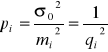
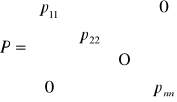
Funkcja celu ma postać: V^TPV = min (zgodnie z metodą najmniejszych kwadratów).

3. Obliczamy wartości wyrównane niewiadomych pośredniczących, poprawki obserwacji i wyrównane obserwacje:

X = (A^TPA)^-1A^TPL

Q = (A^TPA)^-1 - oznaczenie: macierz kofaktorów, czyli oszacowań błędów niewiadomych

pośredniczących

V = AX - L

Kontrola obliczeń: A^TPV = 0

4. Obliczamy błędy.

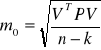
estymator współczynnika skali σ₀

Cx = m₀²Q = m₀²(A^TPA)^-1 macierz wariancyjno - kowariancyjna

oszacowanie błędu pojedynczej wartości (błąd pojedynczej

niewiadomej)

błąd obserwacji wyrównanych (macierz wariancyjno -

kowariancyjna wektora po wyrównaniu)

macierz wariancyjno - kowariancyjna wektora poprawek

C_L = m₀²P^-1 macierz błędu wektora przed wyrównaniem

Koniec oceny dokładności.

5. Sprawdzenie jakości wyrównania i jakości danych

1. porównanie wyliczonego współczynnika skali (m₀) z współczynnikiem skali przyjętym do wyrównania (do wagowania, σ₀):

2. testem χ² (chi²) sprawdzamy zgodność wariancji (??)

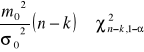
3. znalezienie błędów grubych

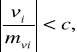
gdzie: c - stała (1, 2 lub 3)

m_vi - błąd poprawki (obliczany z C_V )

---