DZIEL I ZWYCIĘŻAJ

W teorii obliczeń dziel i zwyciężaj (ang. divide and conquer) jest ważną strategią konstruowania algorytmów i jedną z najefektywniejszych metod algorytmicznych w informatyce. W strategii tej problem dzieli się rekurencyjnie na dwa lub więcej mniejszych podproblemów tego samego (lub podobnego) typu tak długo, aż fragmenty staną się wystarczająco proste do bezpośredniego rozwiązania. Z kolei rozwiązania otrzymane dla podproblemów scala się uzyskując rozwiązanie całego zadania.

Klasyczne przykłady algorytmów korzystających z tej metody to m.in. sortowanie przez scalanie (mergesort), sortowanie szybkie (quicksort), wyszukiwanie binarne.

Sortowanie przez scalanie

Wyróżnić można trzy podstawowe kroki:

1. Podziel zestaw danych na dwie, równe części (w przypadku nieparzystej liczby wyrazów jedna część będzie o 1 wyraz dłuższa);

2. Zastosuj sortowanie przez scalanie dla każdej z nich oddzielnie, chyba że pozostał już tylko jeden element;

3. Połącz posortowane podciągi w jeden.

Procedura scalania dwóch ciągów A[1..n] i B[1..m] do ciągu C[1..m+n]:

1. Utwórz wskaźniki na początki ciągów A i B → i=0, j=0

2. Jeżeli A[i] < = B[j] wstaw A[i] do C i zwiększ i o jeden, w przeciwnym przypadku wstaw B[j] do C i zwiększ j o jeden

3. Powtarzaj krok 2 aż wszystkie wyrazy A i B trafią do C

Scalenie wymaga O(n+m) operacji porównań elementów i wstawienia ich do tablicy wynikowej.

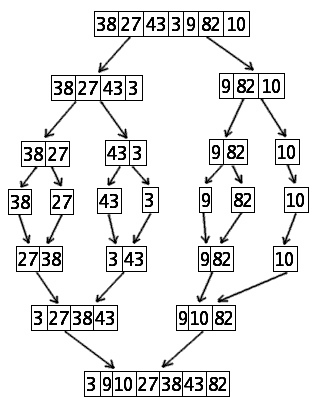
Graficzne przedstawienie

metody sortowania

przez scalanie.

Sortowanie szybkie

Algorytm działa rekursywnie - wybierany jest pewien element tablicy, tzw. element osiowy, po czym na początek tablicy przenoszone są wszystkie elementy mniejsze od niego, na koniec wszystkie większe, a w powstałe między tymi obszarami puste miejsce trafia wybrany element. Potem sortuje się osobno początkową i końcową część tablicy. Rekursja kończy się, gdy kolejny fragment uzyskany z podziału zawiera pojedynczy element, jako że jednoelementowa podtablica nie wymaga sortowania.

Implementacja w języku C++ przy założeniu, że elementem osiowym jest środkowy element tablicy.

void quicksort(int tab[], int left, int right)

{

int i=left;

int j=right;

int x=tab[(left+right)/2];

do{

while(tab[i]<x) i++;

while(tab[j]>x) j--;

if(i<=j){

int temp=tab[i];

tab[i]=tab[j];

tab[j]=temp;

i++;

j--;

}

}while(i<=j);

if(left<j) quicksort(tab,left,j);

if(right>i) quicksort(tab,i,right);

}

Wyszukiwanie binarne

Uporządkowana tablica jest dzielona na coraz mniejsze przedziały do momentu, gdy szukany element zostanie znaleziony, bądź przedział osiągnie długość zero, co oznacza brak elementu.

W pojedynczym kroku rozważa się jeden przedział charakteryzowany dwoma indeksami: początkowym a i końcowym b. Algorytm rozpoczyna wyszukiwanie od całej tablicy.

Następnie wyznaczany jest środek tego przedziału c=(a+b)/2 . Wówczas testowane jest, czy element zapisany pod indeksem c jest tym poszukiwanym — jeśli tak, to algorytm w tym miejscu kończy działanie.

W przeciwnym razie przedział jest zawężany - dzięki uporządkowaniu danych wiadomo, że albo poszukiwany element może znajdować się gdzieś przed indeksem c albo za nim. Innymi słowy wybór ogranicza się do przedziału [a,c − 1], gdy poszukiwany element jest mniejszy od zapisanego pod indeksem c, albo [c + 1,b] w przeciwnym razie.

Algorytm kończy się niepowodzeniem, jeśli przedział będzie pusty, tzn. b < a (lewy koniec przedziału "znajdzie się" za prawym końcem).

2

---