1

Wykład 3

Metoda „dziel i

zwyciężaj”

2

Wprowadzenie

 Technika konstrukcji algorytmów

dziel i zwyciężaj.

 przykładowe problemy:

– Wypełnianie planszy
– Poszukiwanie (binarne)
– Sortowanie (sortowanie przez łączenie - merge sort).

3

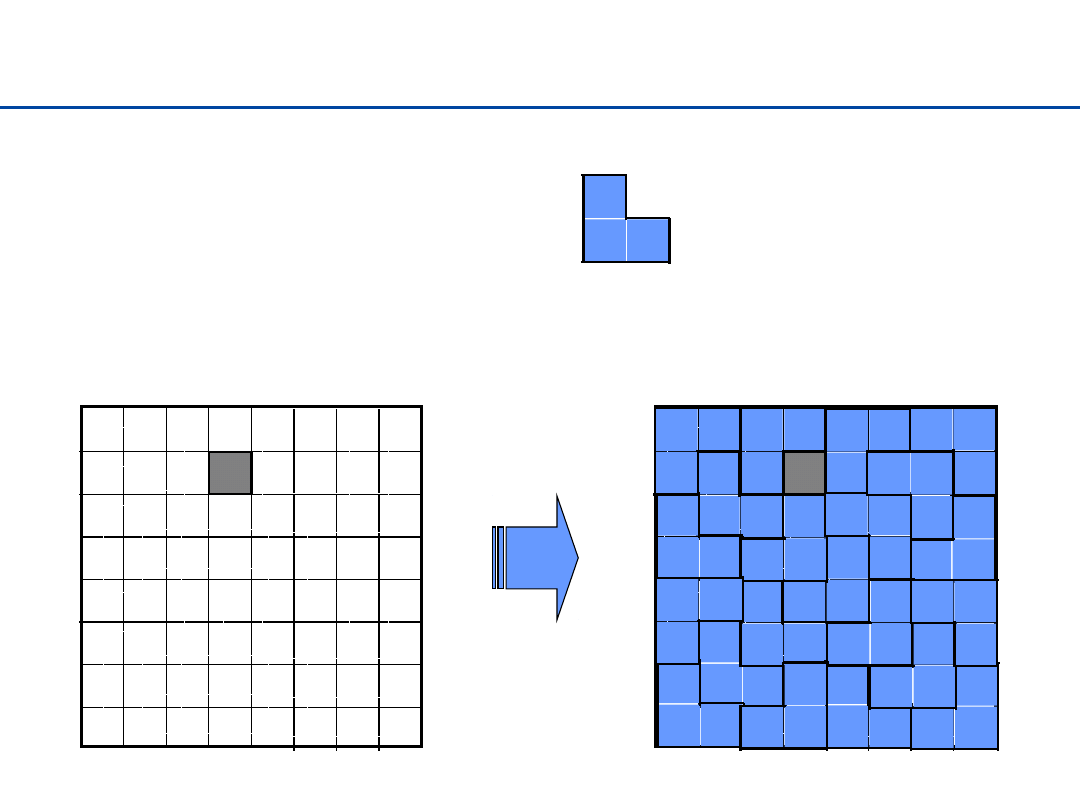
Wypełnianie planszy

Zadanie: dysponując klockami

oraz planszą
2

n

x2

n

z

brakującym
polem:

Wypełnić plansze
w całości:

4

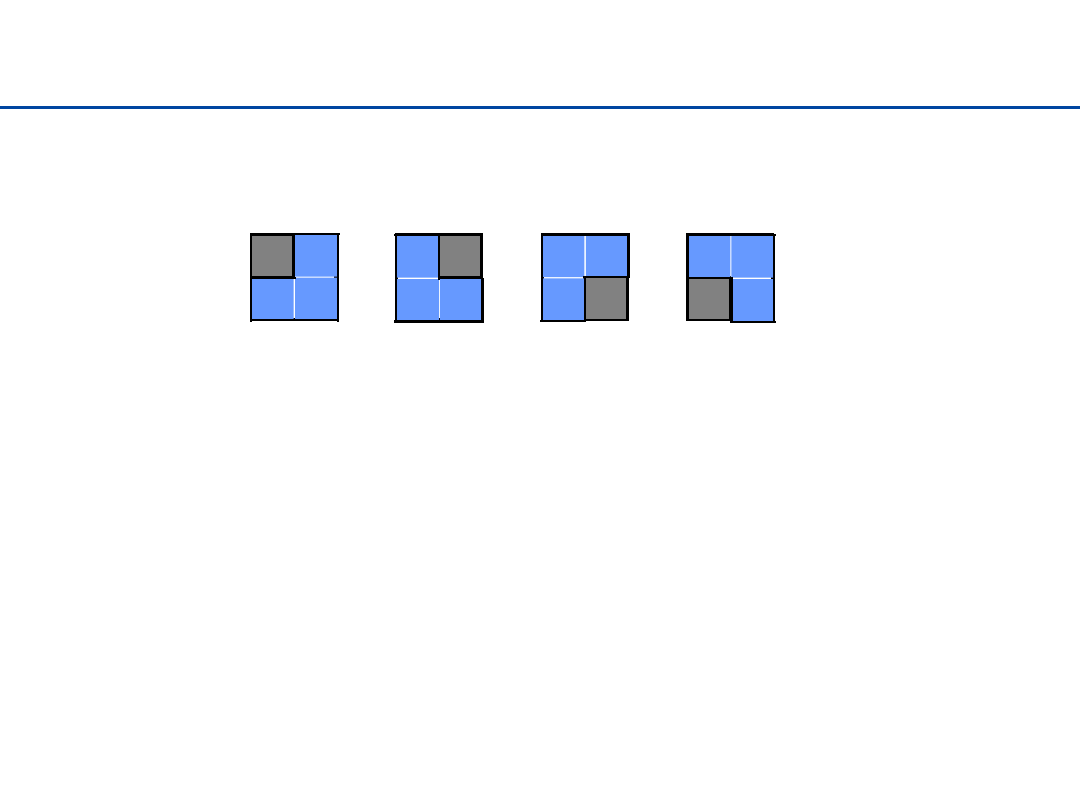
Wypełnianie planszy: przypadki trywialne (n = 1)

 Przypadek trywialny (n = 1): wypełniamy plansze jednym

klockiem:



Idea dla rozwiązania problemu – doprowadzić
rozmiar zadania do przypadku trywialnego,
który umiemy rozwiązać

5

Wypełnianie planszy : podział zadania

 Oryginalną planszę dzielimy na 4 części



Dostajemy problemy o rozmiarze 2

n-1

x2

n-

1



Ale: trzy z nich nie są podobne do
oryginalnego (plansze nie mają
brakującego pola)!

6

Wypełnianie planszy : podział zadania

 pomysł: umieszczamy jeden klocek w środku planszy i

dokonujemy podziału na 4 części



Teraz otrzymujemy 4 plansze o rozmiarach 2

n-1

x2

n-1

.



Każda z planszy ma brakujące pole

7

Wypełnianie planszy : algorytm

INPUT: n – plansza 2

n

x2

n

, L – pozycja brakującego pola.

OUTPUT: wypełniona plansza

Tile(n, L)
if n = 1 then
przypadek trywialny
wypełnij jednym klockiem
return
umieść jeden klocek w środku planszy

podziel planszę na 4 równe części
Niech L1, L2, L3, L4 oznaczają pozycje 4 brakujących pól

Tile(n-1, L1)
Tile(n-1, L2)
Tile(n-1, L3)
Tile(n-1, L4)

INPUT: n – plansza 2

n

x2

n

, L – pozycja brakującego pola.

OUTPUT: wypełniona plansza

Tile(n, L)
if n = 1 then

przypadek trywialny

wypełnij jednym klockiem
return
umieść jeden klocek w środku planszy

podziel planszę na 4 równe części
Niech L1, L2, L3, L4 oznaczają pozycje 4 brakujących pól

Tile(n-1, L1)
Tile(n-1, L2)
Tile(n-1, L3)
Tile(n-1, L4)

8

Dziel i zwyciężaj

 Metoda konstrukcji algorytmów „Dziel i zwyciężaj” :

– Jeśli problem jest na tyle mały, że umiesz go rozwiązać - zrób to.

Jeśli nie to:

• Podział: Podziel problem na dwa lub więcej rozdzielnych

podproblemów

• Rozwiązanie: Wykorzystaj metodę rekurencyjnie dla

rozwiązania tych podproblemów

• Łączenie: połącz rozwiązania podproblemów tak, aby

rozwiązać oryginalny problem

9

Wypełnianie planszy : Dziel i zwyciężaj

 Wypełnianie jest przykładem algorytmu „dziel i zwyciężaj” :

– w wypadku trywialnym (2x2) – po prostu wypełniamy planszę, lub:
– Dzielimy planszę na 4 mniejsze części (wprowadzając wypełnione

miejsce w rogu, przez umieszczenie centralnie jednego klocka)

– Rozwiązujemy problem rekursywnie stosując tą samą metodę
– Łączymy części umieszczając klocek w środku planszy

10

 Odnaleźć

liczbę w posortowanej tablicy:

– Przypadek trywialny – tablica jest jednoelementowa
– Albo dzielimy tablice na dwie równe części i rozwiązujemy

zadanie osobno dla każdej z

nich

Poszukiwanie binarne

INPUT: A[1..n] – posortowana niemalejąco tablica liczb, s – liczba.
OUTPUT: indeks j taki, że A[j] = s. NIL, jeśli j (1jn): A[j] s
Binary-search(A, p, r, s):
if p = r then
if A[p] = s then return p
else return NIL
q(p+r)/2
ret  Binary-search(A, p, q, s)
if ret = NIL then
return Binary-search(A, q+1, r, s)
else return ret

INPUT: A[1..n] – posortowana niemalejąco tablica liczb, s – liczba.
OUTPUT: indeks j taki, że A[j] = s. NIL, jeśli j (1jn): A[j] s
Binary-search(A, p, r, s):
if p = r then
if A[p] = s then return p
else return NIL
q(p+r)/2
ret  Binary-search(A, p, q, s)
if ret = NIL then
return Binary-search(A, q+1, r, s)
else return ret

11

Rekurencja

 Czas działania algorytmu z odwołaniami rekursywnymi można opisać

poprzez rekurencję

 Równanie/nierówność opisująca funkcję poprzez jej wartości dla

mniejszego argumentu

Przykład: poszukiwanie binarne

(1)

if

1

( )

2 ( / 2)

(1) if

1

n

T n

T n

n









 





12

Poszukiwanie binarne (poprawione)

INPUT: A[1..n] – posortowana niemalejąco tablica liczb, s – liczba.
OUTPUT: indeks j taki, że A[j] = s. NIL, jeśli j (1≤j≤n): A[j] ≠s

Binary-search(A, p, r, s):
if p = r then
if A[p] = s then return p
else return NIL
q(p+r)/2
if A[q]  s then return Binary-search(A, p, q, s)
else return Binary-search(A, q+1, r, s)

INPUT: A[1..n] – posortowana niemalejąco tablica liczb, s – liczba.
OUTPUT: indeks j taki, że A[j] = s. NIL, jeśli j (1≤j≤n): A[j] ≠s

Binary-search(A, p, r, s):
if p = r then
if A[p] = s then return p
else return NIL
q(p+r)/2
if A[q]  s then return Binary-search(A, p, q, s)
else return Binary-search(A, q+1, r, s)

 T(n) = (n) – nie lepiej niż dla metody siłowej!
 Poprawa: rozwiązywać zadanie tylko dla jednej połowy tablicy

13

Czas działania metody

T(n) = (lg n) !

(1)

if

1

( )

( / 2)

(1) if

1

n

T n

T n

n









 





14

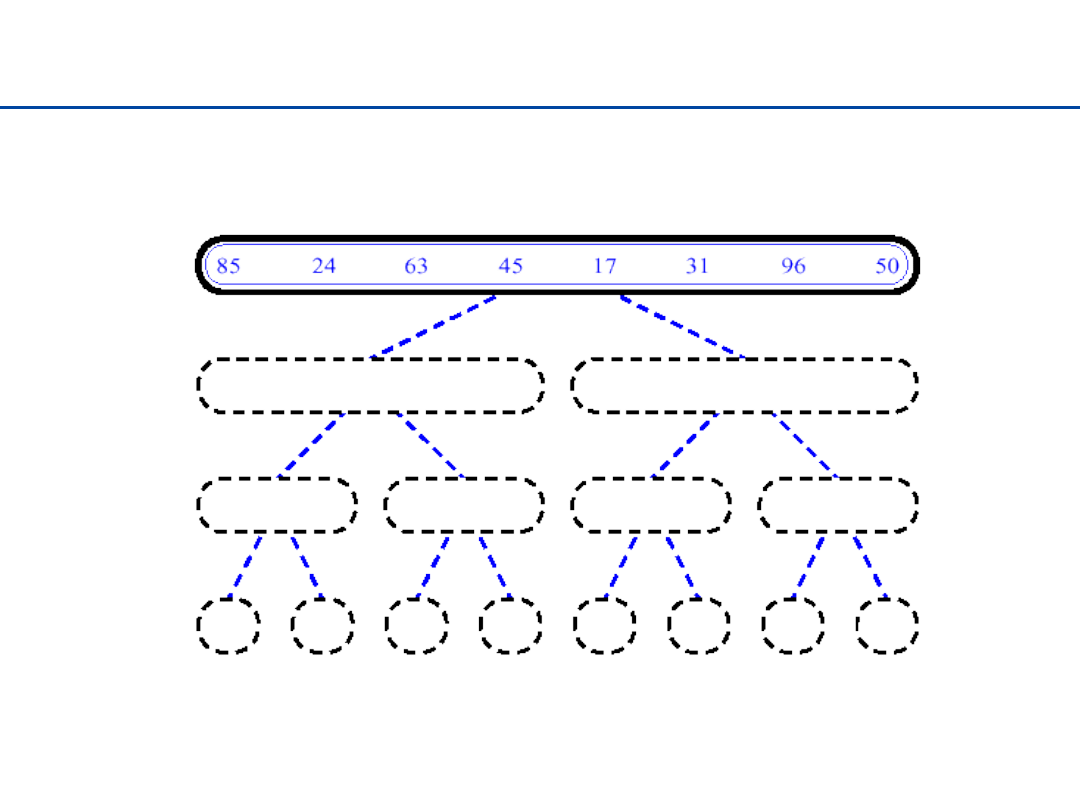
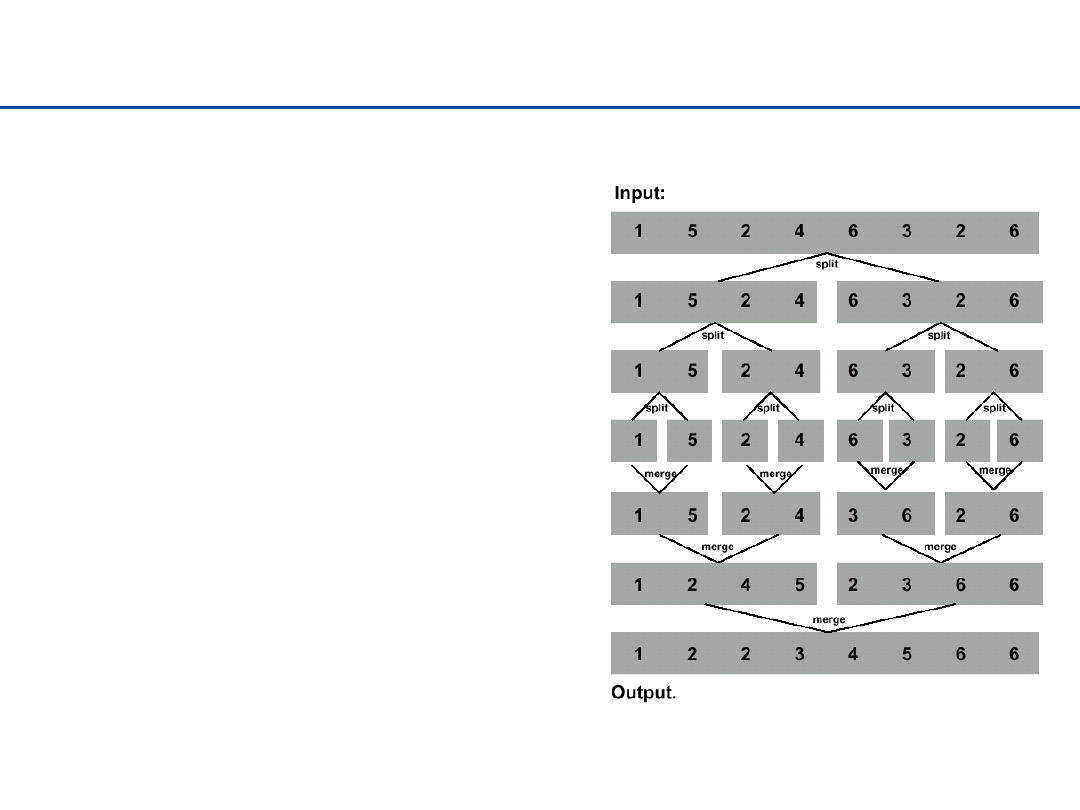
Sortowanie przez łączenie (merge sort)

 Podziel: Jeśli S posiada przynajmniej dwa elementy (1 lub 0

elementów – przypadek trywialny), podziel S na dwie równe (z
dokładnością do 1 elementu) części S

1

i S

2

. (tj. S

1

zawiera

pierwsze n/2elementów, a S

2

kolejne n/2).

 Zwyciężaj: posortuj sekwencje S

1

i S

2

stosując Merge Sort.

 Połącz: Połącz elementy z dwóch posortowanych sekwencji S

1

i

S

2

w sekwencję S zachowaniem porządku

15

Algorytm – Merge Sort

Merge-Sort(A, p, r)
if p < r then
q(p+r)/2

Merge-Sort(A, p, q)
Merge-Sort(A, q+1, r)
Merge(A, p, q, r)

Merge-Sort(A, p, r)
if p < r then
q(p+r)/2

Merge-Sort(A, p, q)
Merge-Sort(A, q+1, r)
Merge(A, p, q, r)

Merge(A, p, q, r)
wybieramy mniejszy z dwóch elementów na początku
sekwencji A[p..q] oraz A[q+1..r] i wkładamy go do
sekwencji wynikowej, przestawiamy odpowiedni znacznik.
Powtarzamy to aż do wyczerpania się elementów.
Rezultat kopiujemy do A[p..r].

Merge(A, p, q, r)
wybieramy mniejszy z dwóch elementów na początku
sekwencji A[p..q] oraz A[q+1..r] i wkładamy go do
sekwencji wynikowej, przestawiamy odpowiedni znacznik.
Powtarzamy to aż do wyczerpania się elementów.
Rezultat kopiujemy do A[p..r].

16

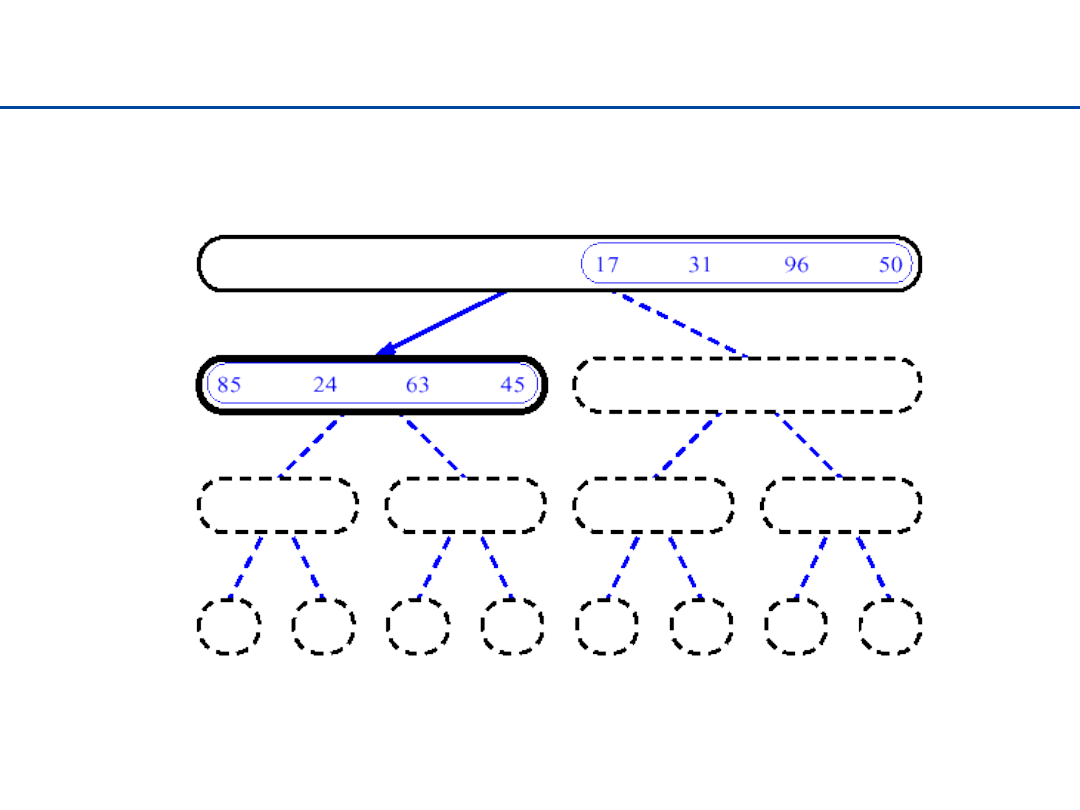
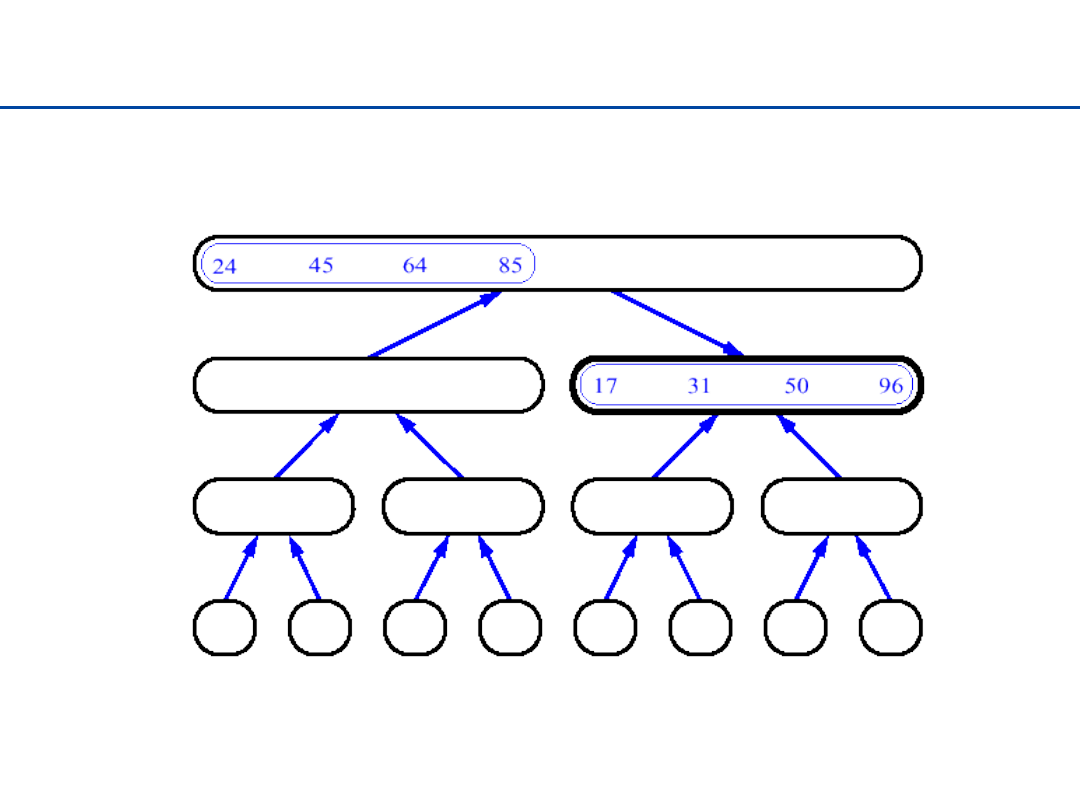
Sortowanie przez łączenie - 1

17

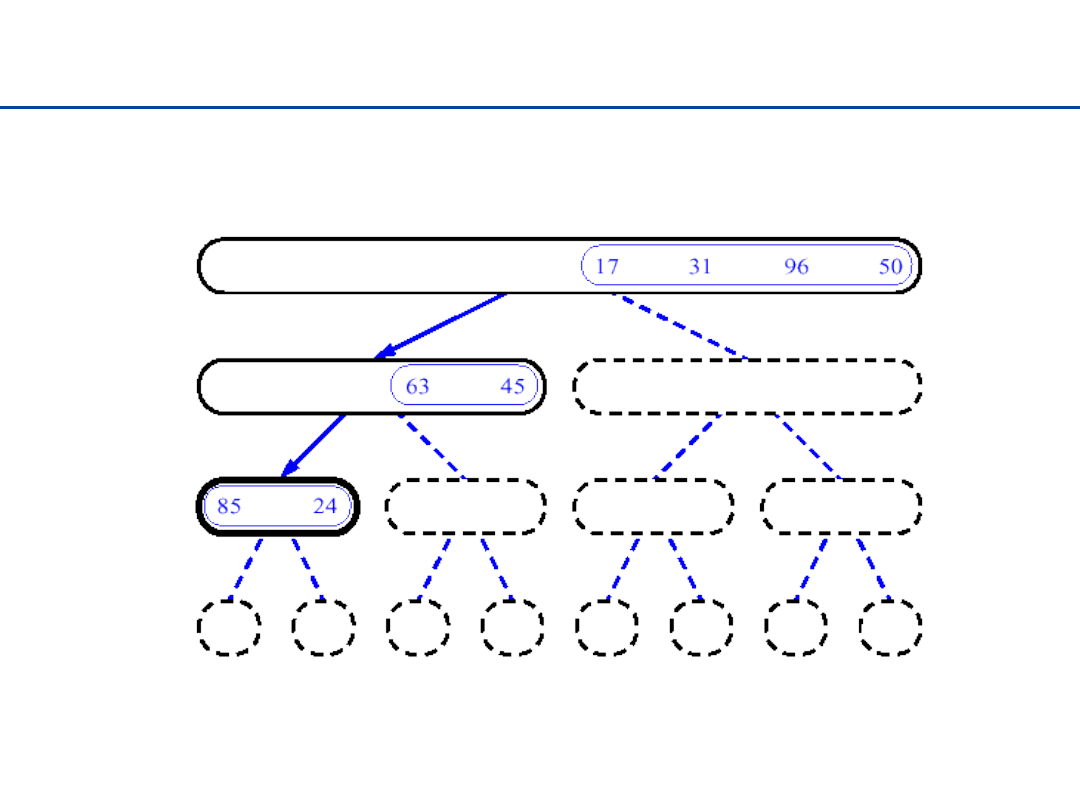
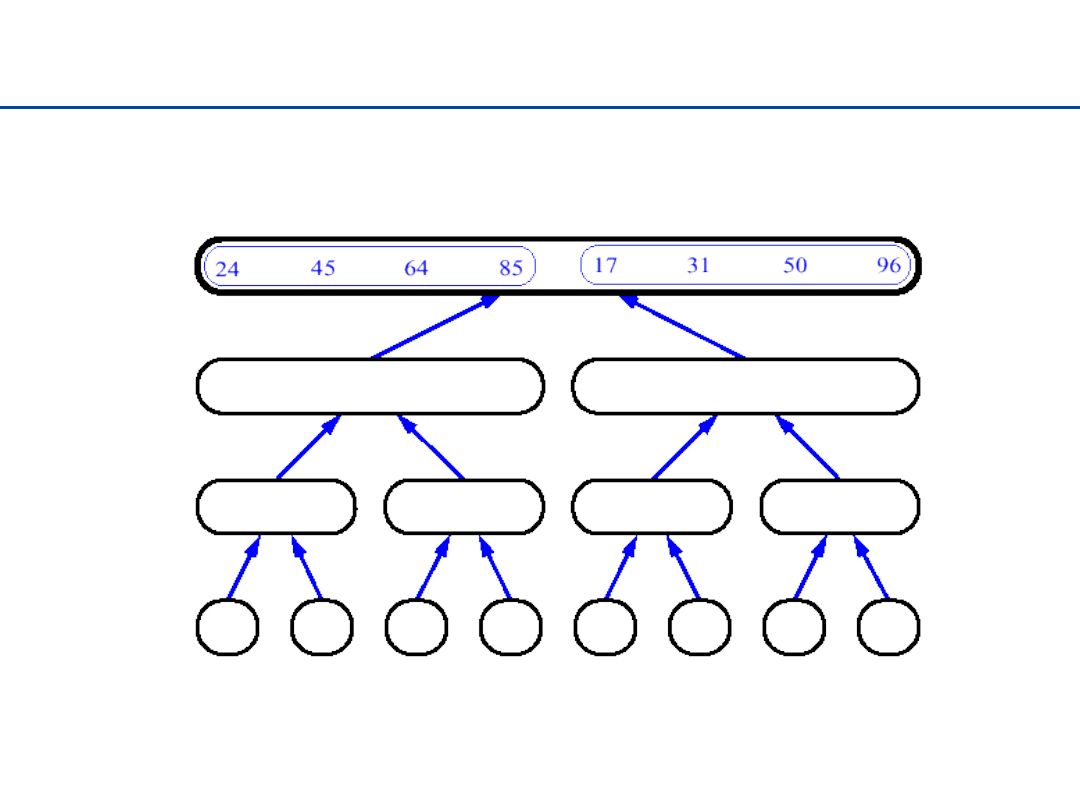
Sortowanie przez łączenie - 2

18

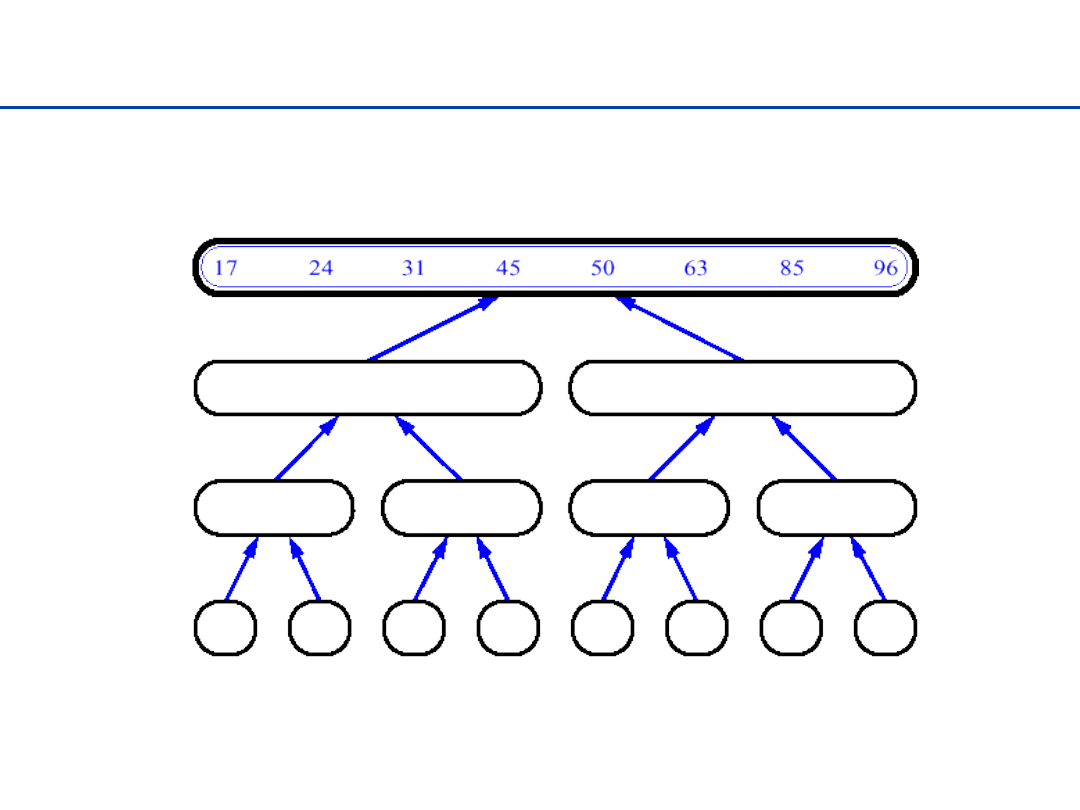
Sortowanie przez łączenie - 3

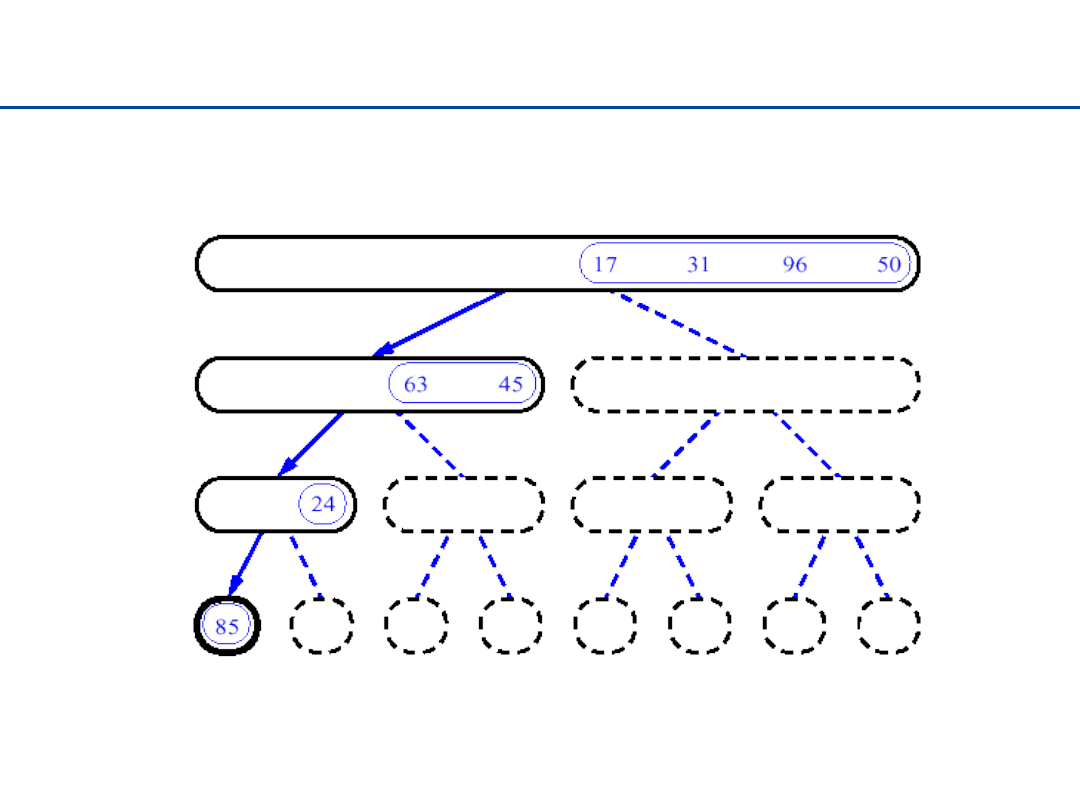
19

Sortowanie przez łączenie - 4

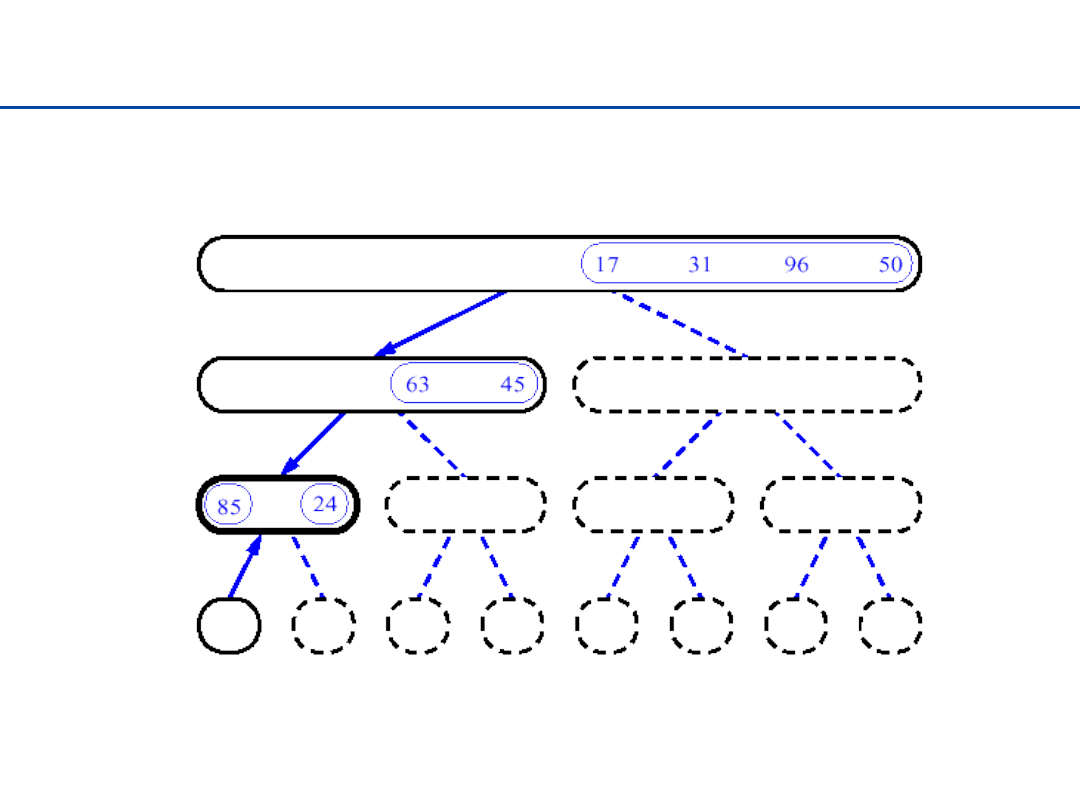
20

Sortowanie przez łączenie - 5

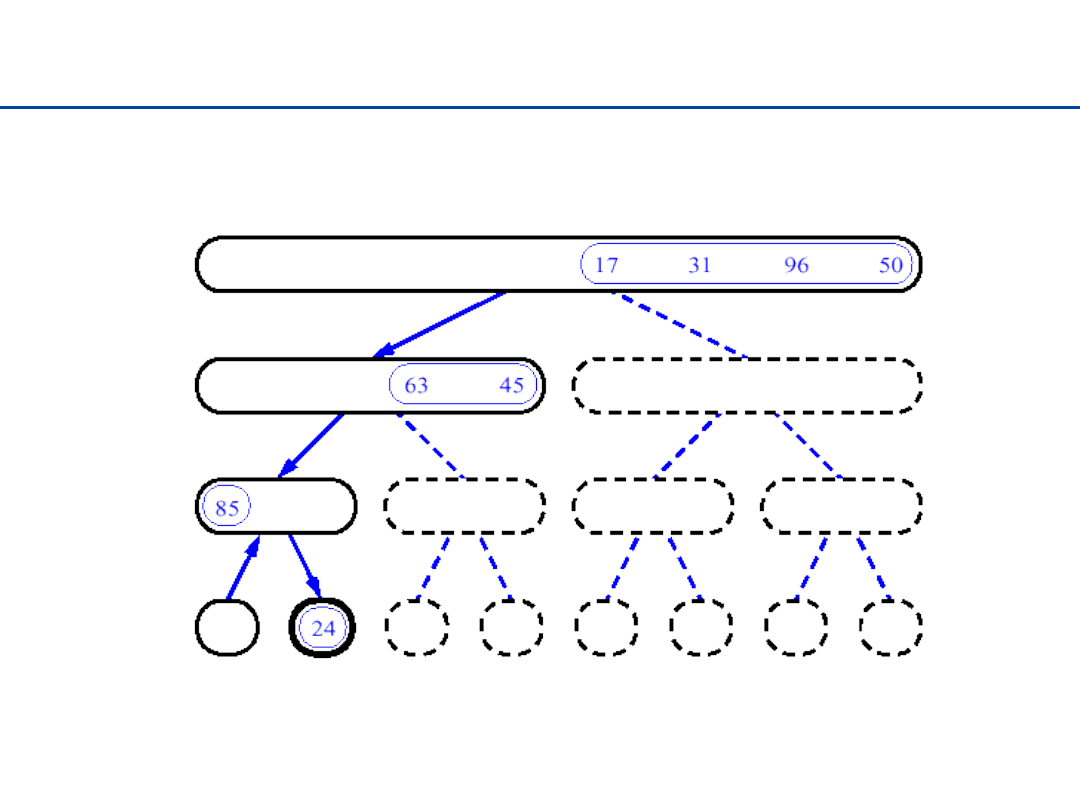
21

Sortowanie przez łączenie - 6

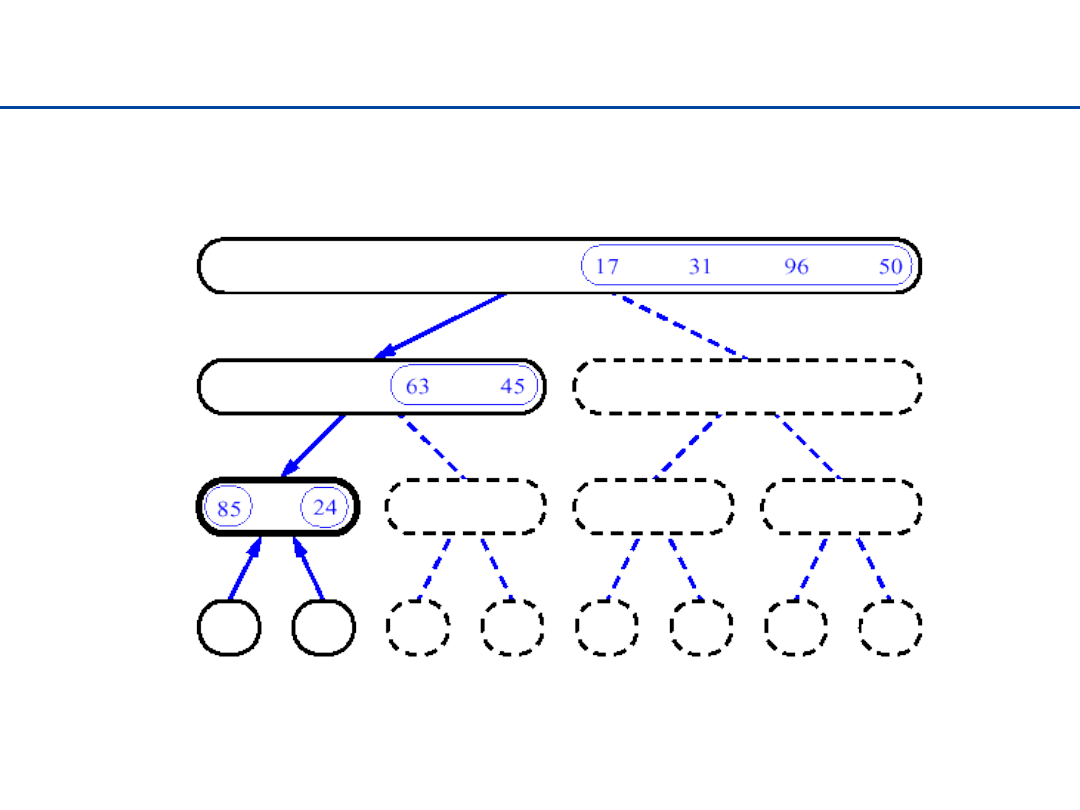
22

Sortowanie przez łączenie - 7

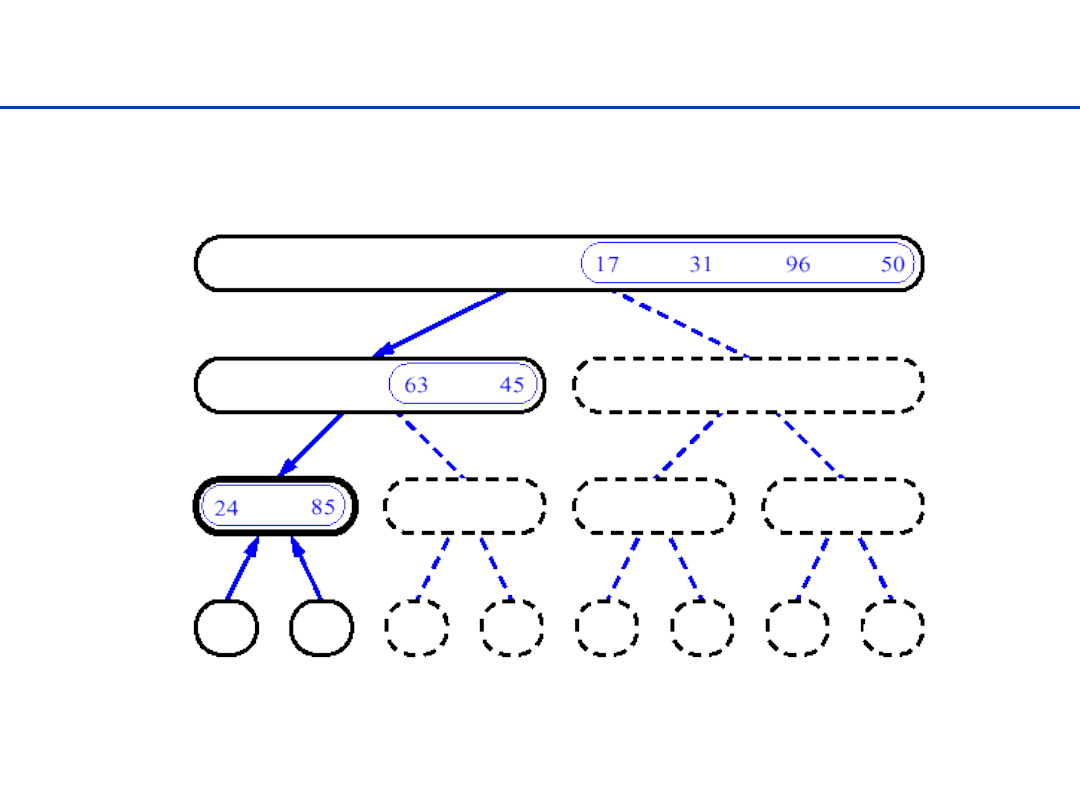
23

Sortowanie przez łączenie - 8

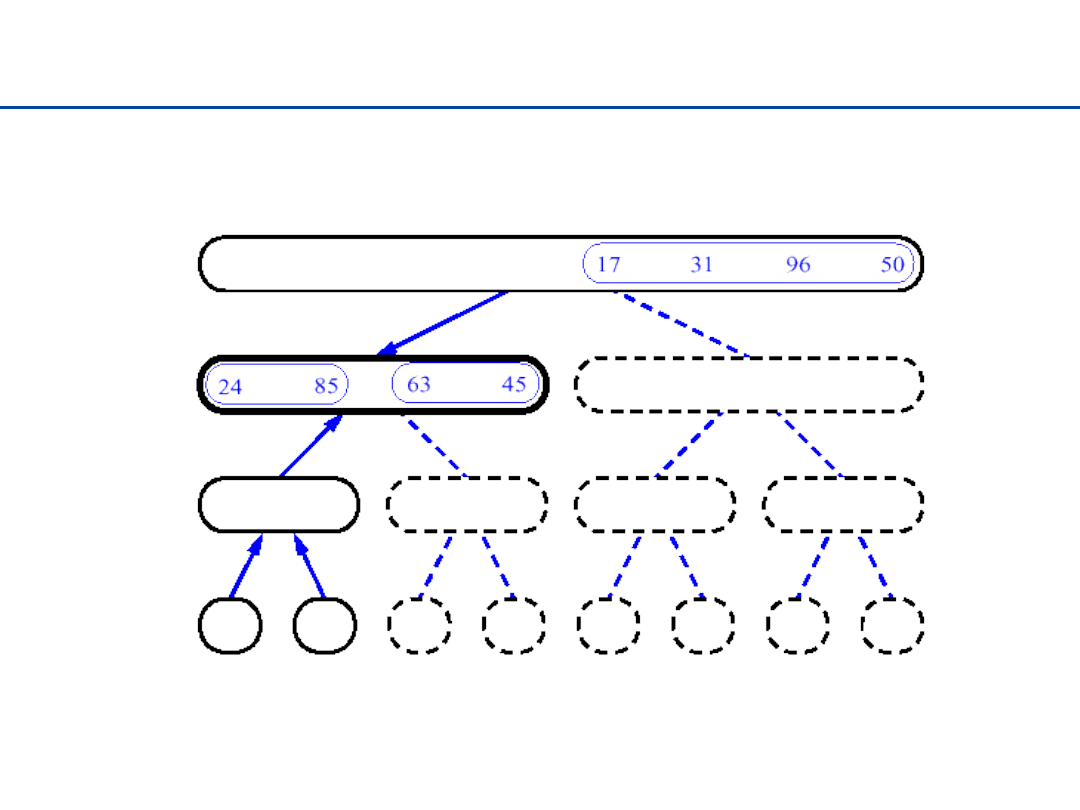
24

Sortowanie przez łączenie - 9

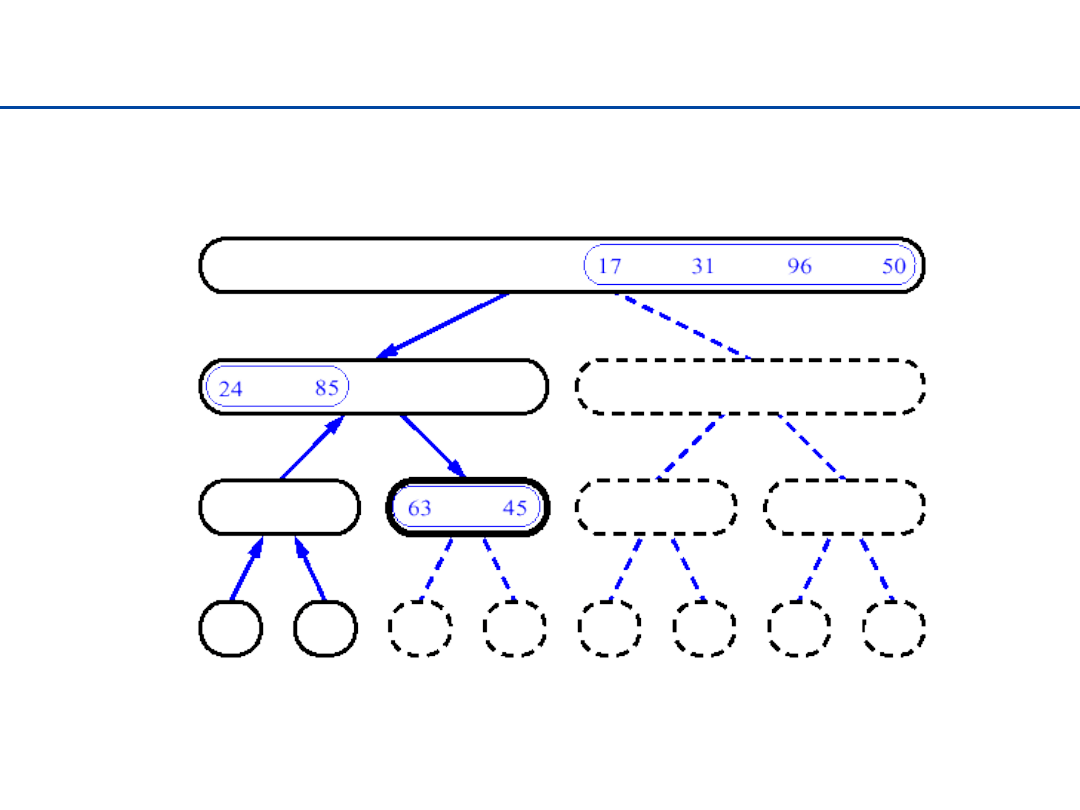
25

Sortowanie przez łączenie - 10

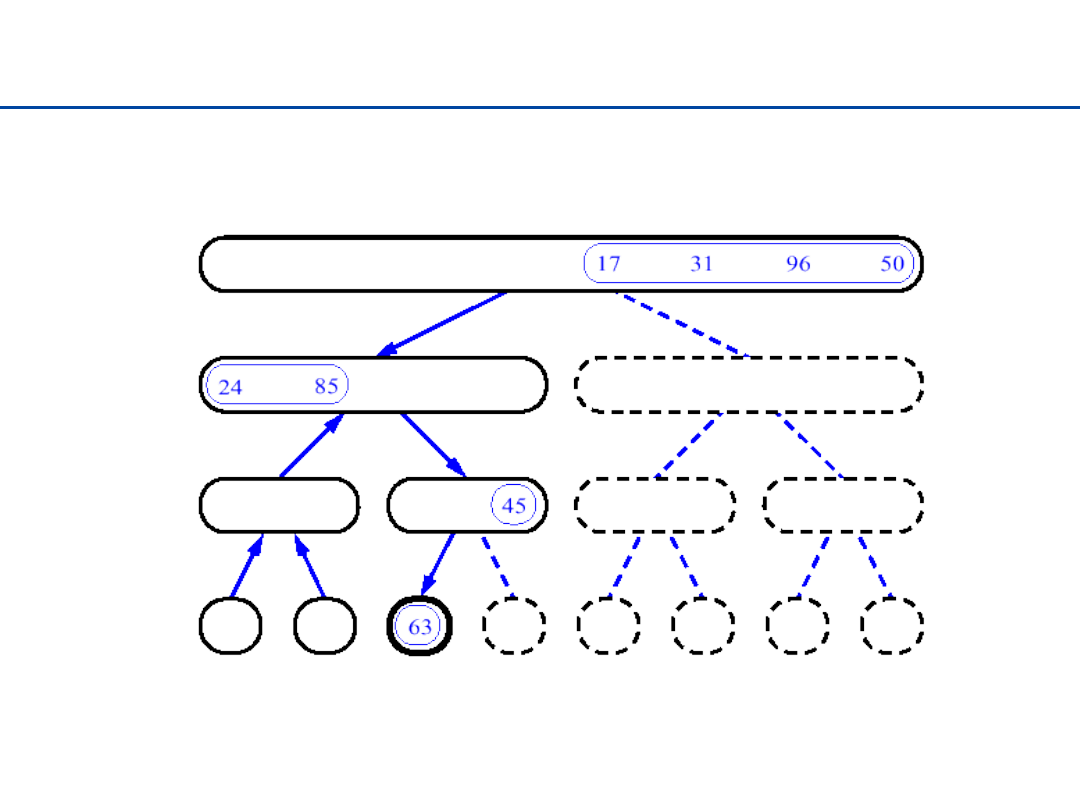
26

Sortowanie przez łączenie - 11

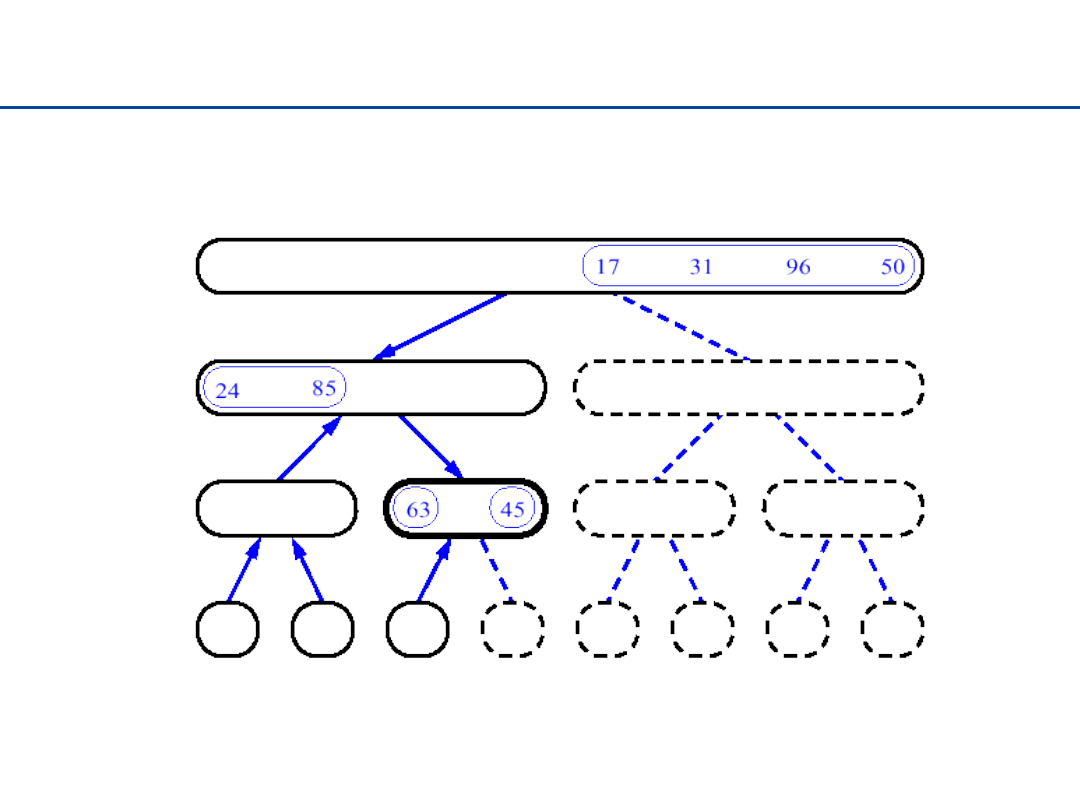
27

Sortowanie przez łączenie - 12

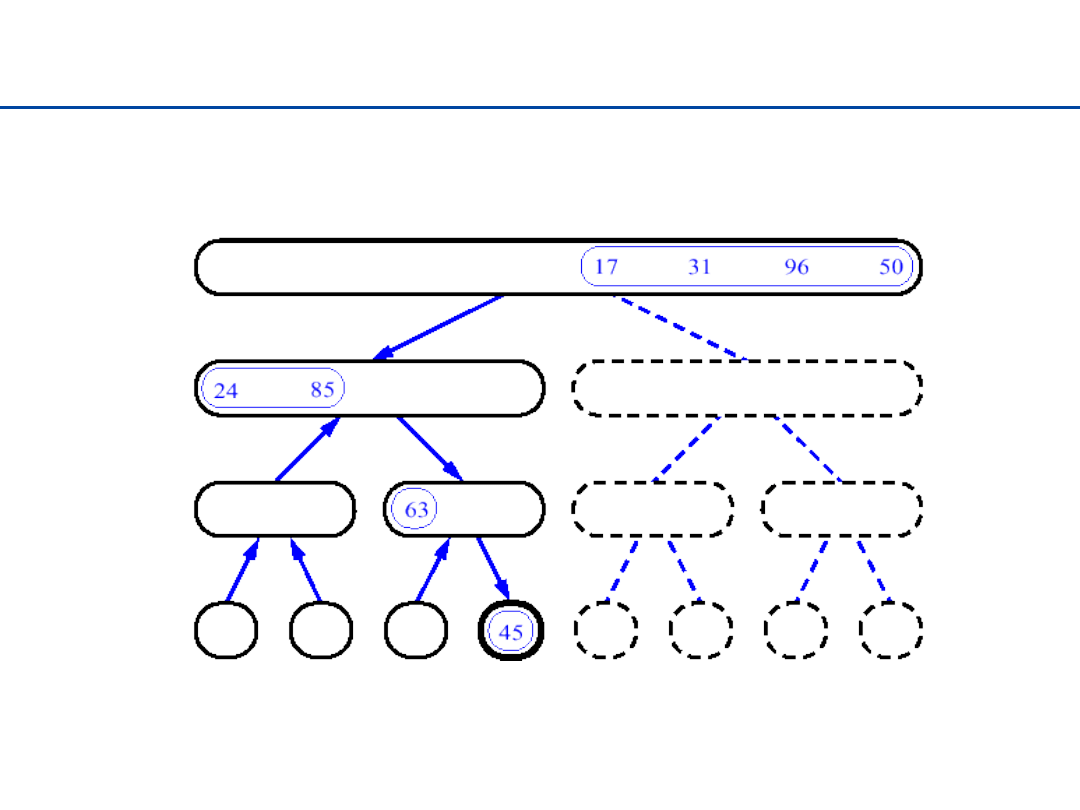
28

Sortowanie przez łączenie - 13

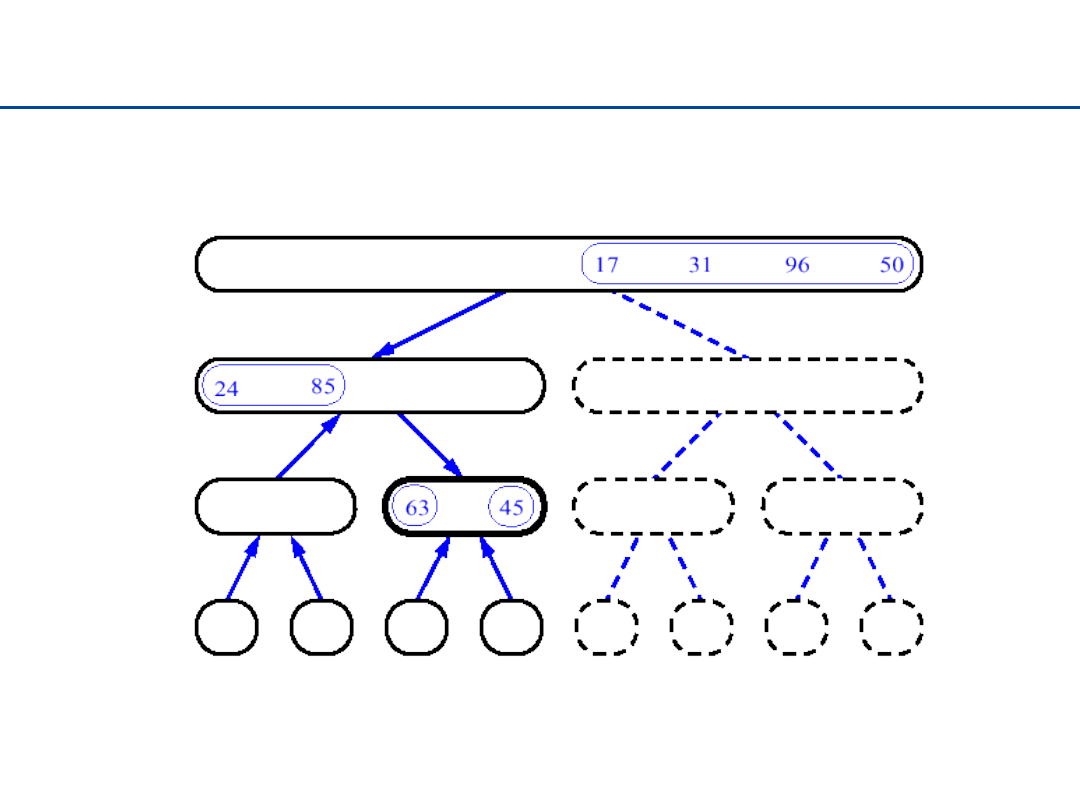
29

Sortowanie przez łączenie - 14

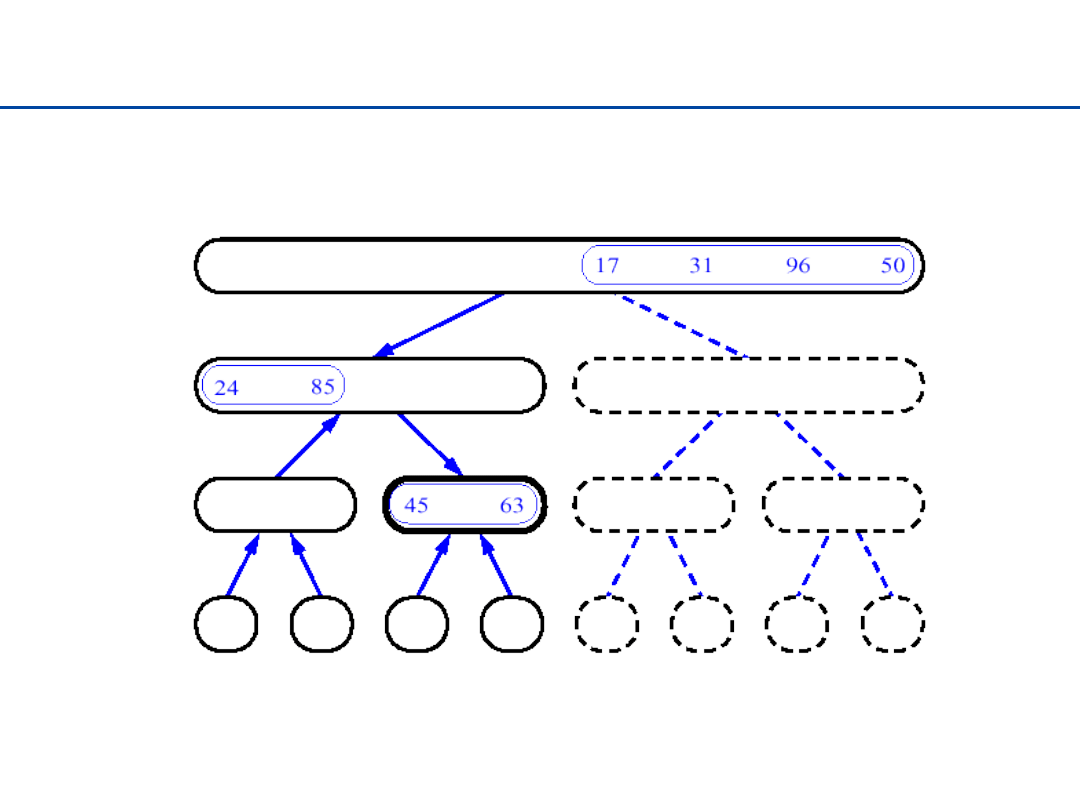
30

Sortowanie przez łączenie - 15

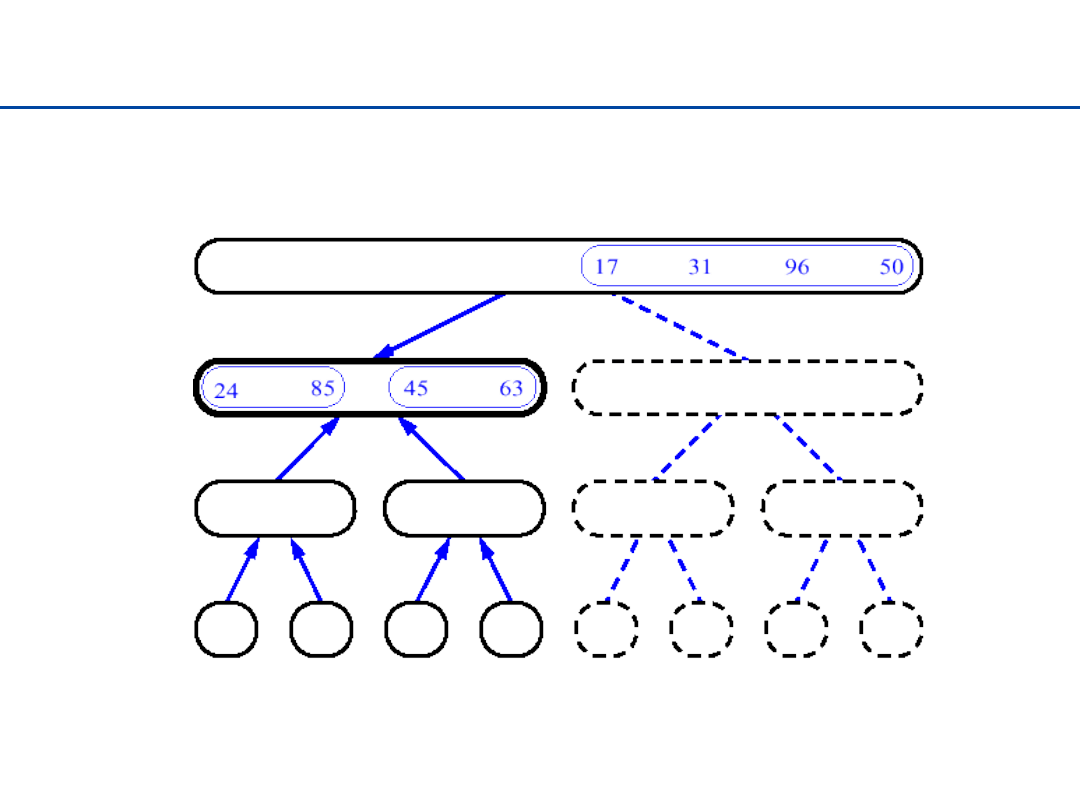
31

Sortowanie przez łączenie - 16

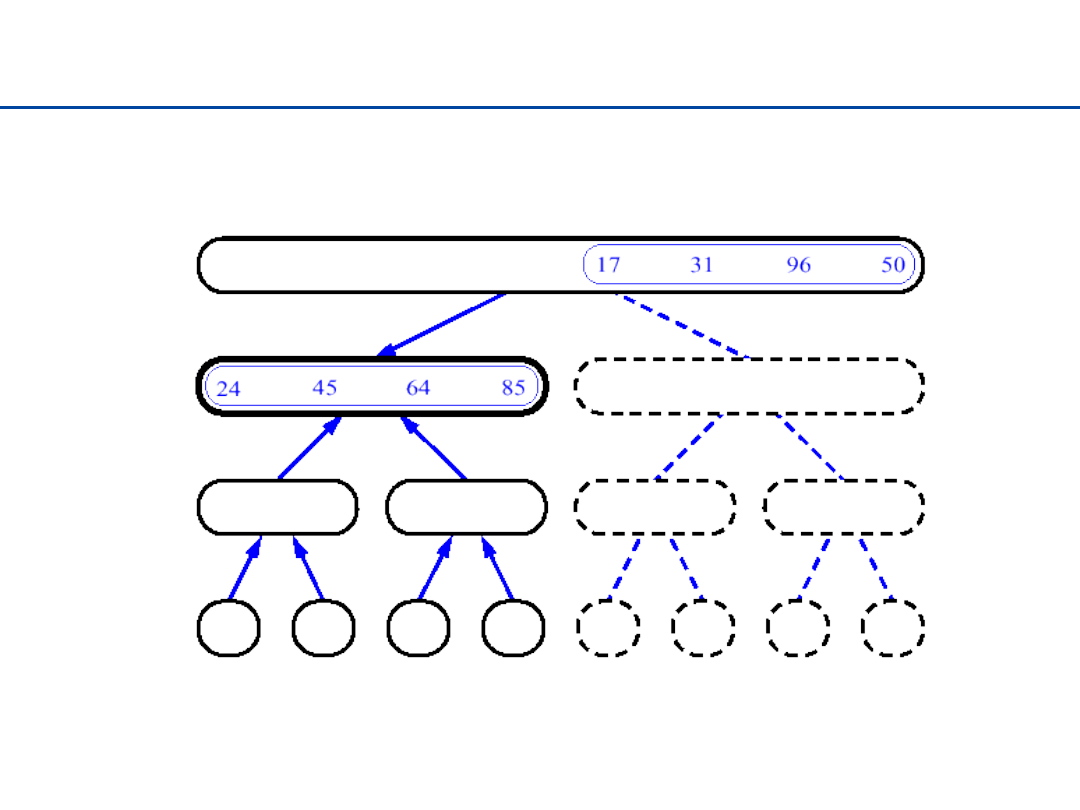
32

Sortowanie przez łączenie - 17

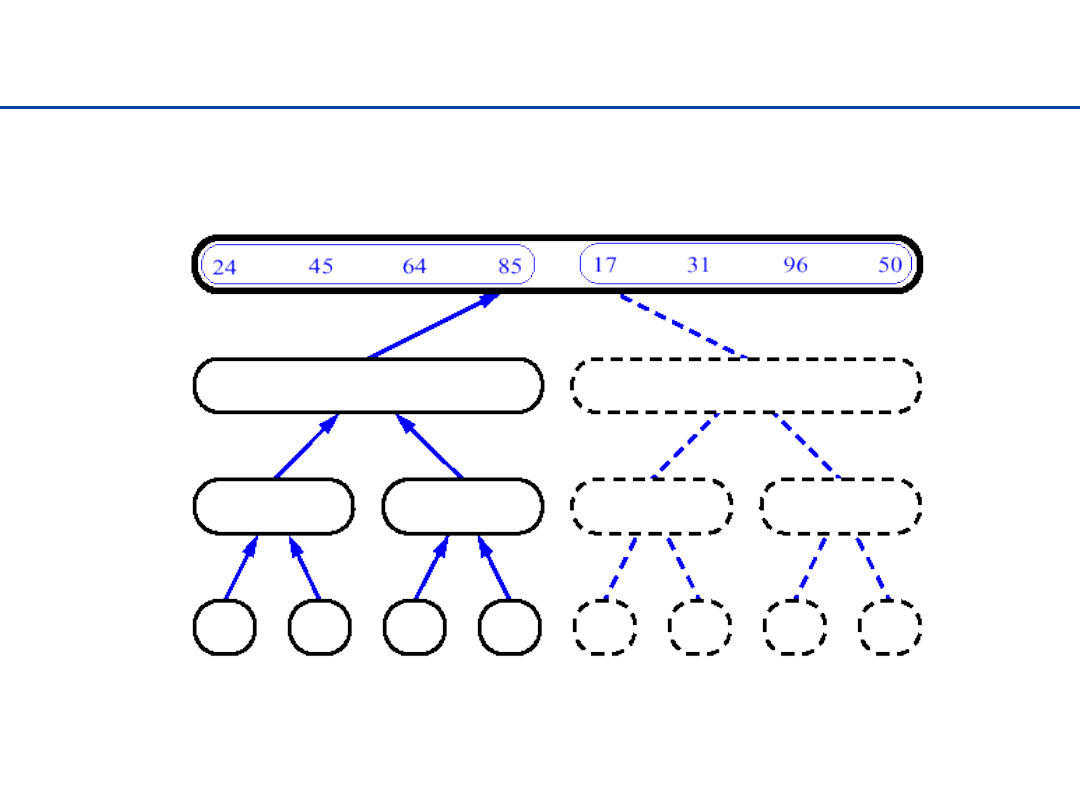
33

Sortowanie przez łączenie - 18

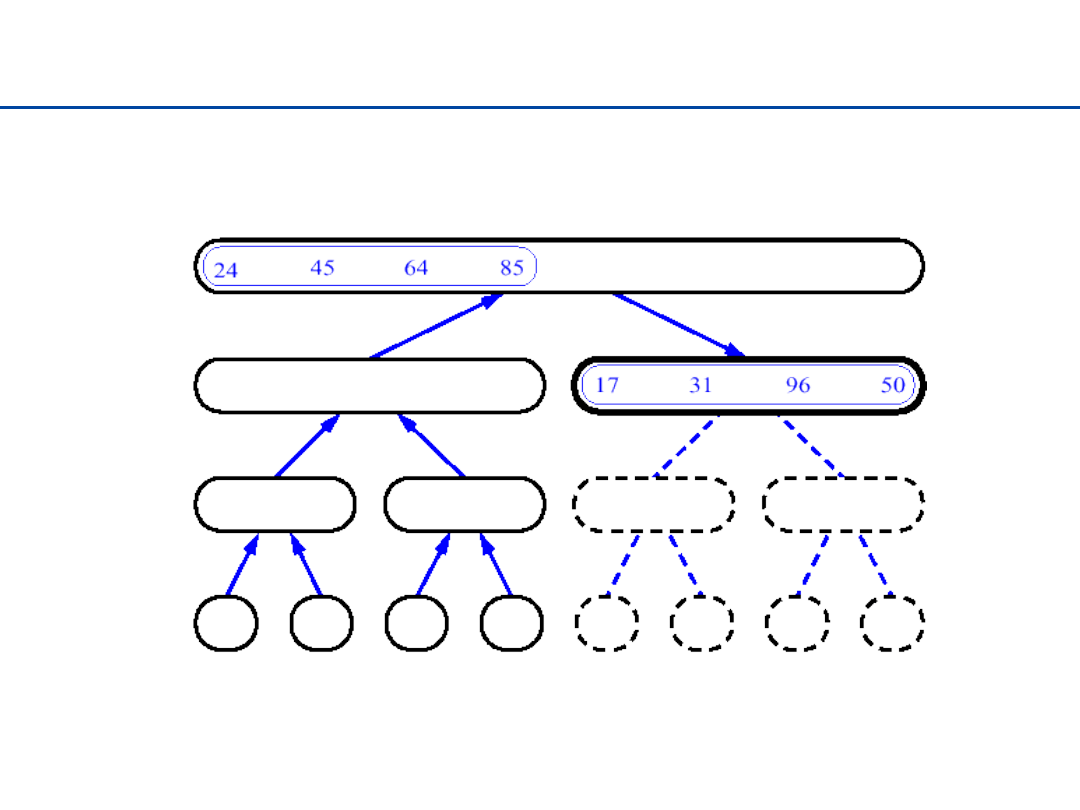
34

Sortowanie przez łączenie - 19

35

Sortowanie przez łączenie - 20

36

Sortowanie przez łączenie - 21

37

Sortowanie przez łączenie - 22

38

Sortowanie przez łączenie – podsumowanie

 Sortowanie n liczb

– jeśli n=1 – trywialne
– rekursywnie sortujemy 2 ciągi

n/2 i n/2 liczb

– łączymy dwa ciągi w czasie (n)

 Strategia

– Podział problemu na mniejsze, ale

analogiczne podproblemy

– Rekursywne rozwiązywanie

podproblemów

– Łączenie otrzymanych rozwiązań

39

Sortowanie przez łączenie – czas działania

 Czas działania algorytmu może

być reprezentowany przez
następującą zależność
rekurencyjną:

 Po rozwiązaniu dostajemy:

(1)

if

1

( )

2 ( /2)

( ) if

1

n

T n

T n

n

n









 





)

lg

(

)

(

n

n

n

T





40

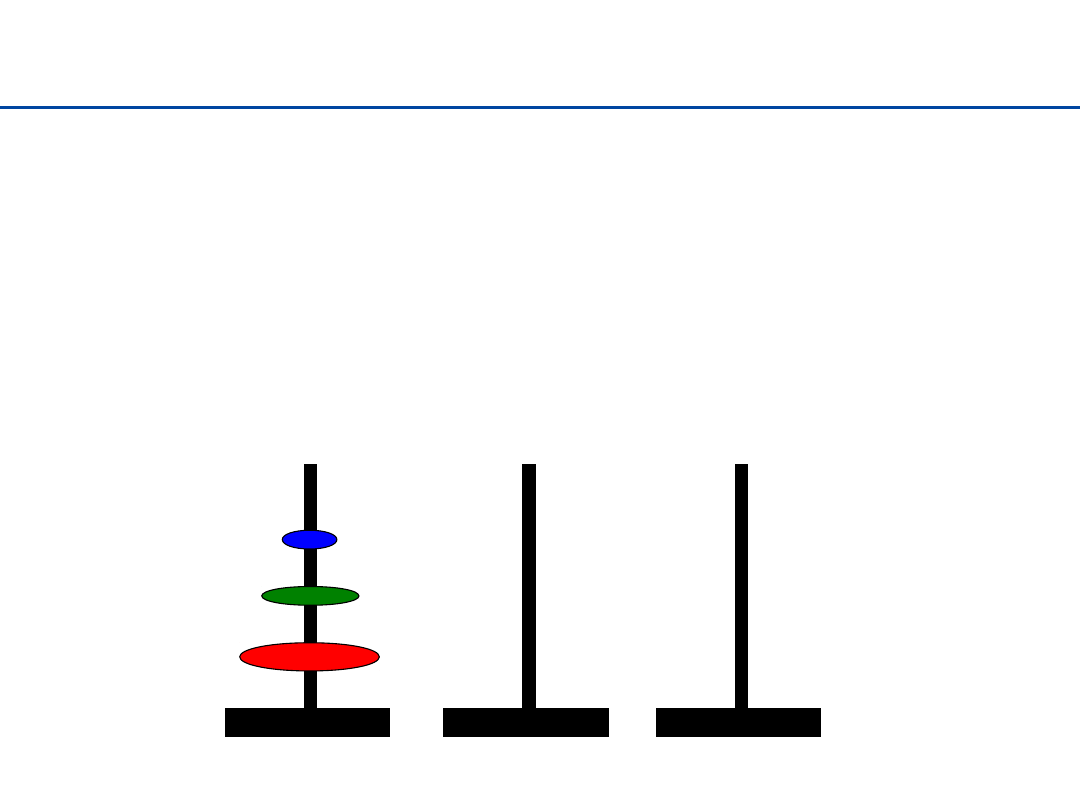
Wieże Hanoi

 Mamy 3 wieże oraz stos 64 dysków o zmniejszających się

średnicach umieszczonych na pierwszej wieży

 Potrzebujemy przenieść wszystkie dyski na inną wieżę
 Zabronione jest położenie dysku większego na mniejszym
 W każdym kroku wolno mam przenieść tylko jeden dysk

41

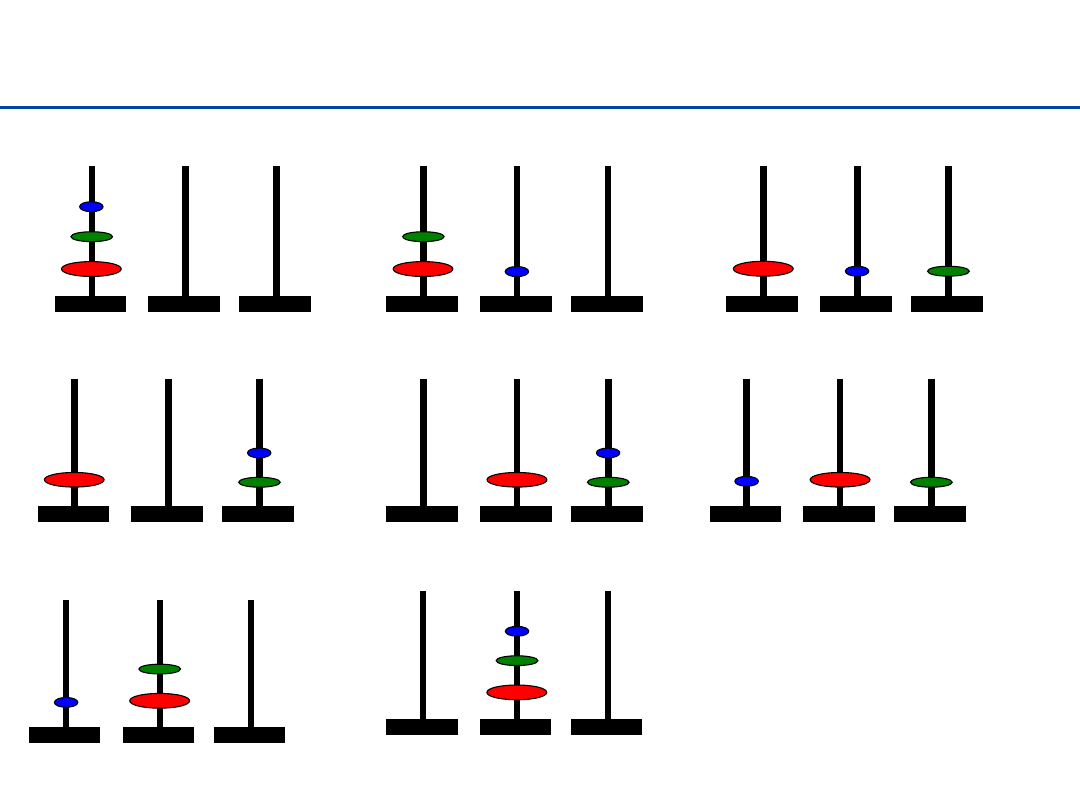
Wieże Hanoi

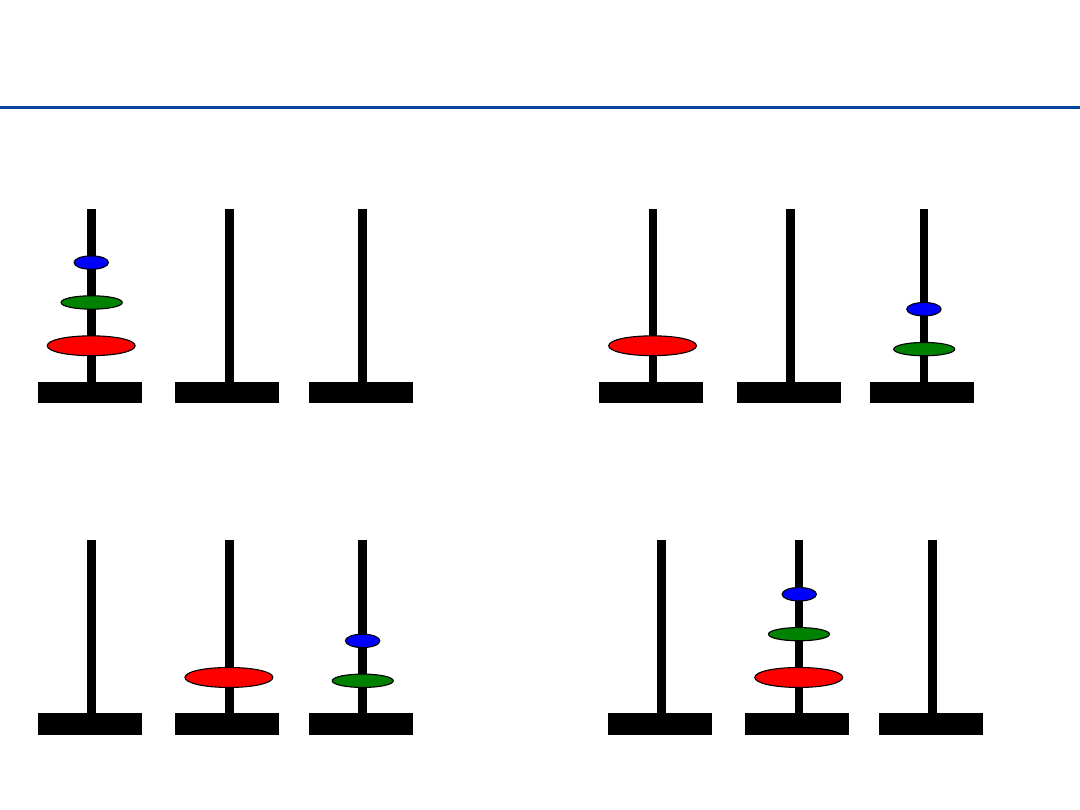
42

Rozwiązanie rekursywne

43

Algorytm rekursywny

INPUT: n – ilość dysków , a, b, c – wieże, wieża a zawiera wszystkie

dyski.

OUTPUT: a, b, c – wieże, wieża b zawiera wszystkie dyski

Hanoi(n, a, b, c)
if n = 1 then
Move(a,b);
else
Hanoi(n-1,a,c,b);
Move(a,b);
Hanoi(n-1,c,b,a);

INPUT: n – ilość dysków , a, b, c – wieże, wieża a zawiera wszystkie

dyski.

OUTPUT: a, b, c – wieże, wieża b zawiera wszystkie dyski

Hanoi(n, a, b, c)
if n = 1 then
Move(a,b);
else
Hanoi(n-1,a,c,b);
Move(a,b);
Hanoi(n-1,c,b,a);

Poprawność algorytmu łatwo pokazać przez indukcję względem n.

44

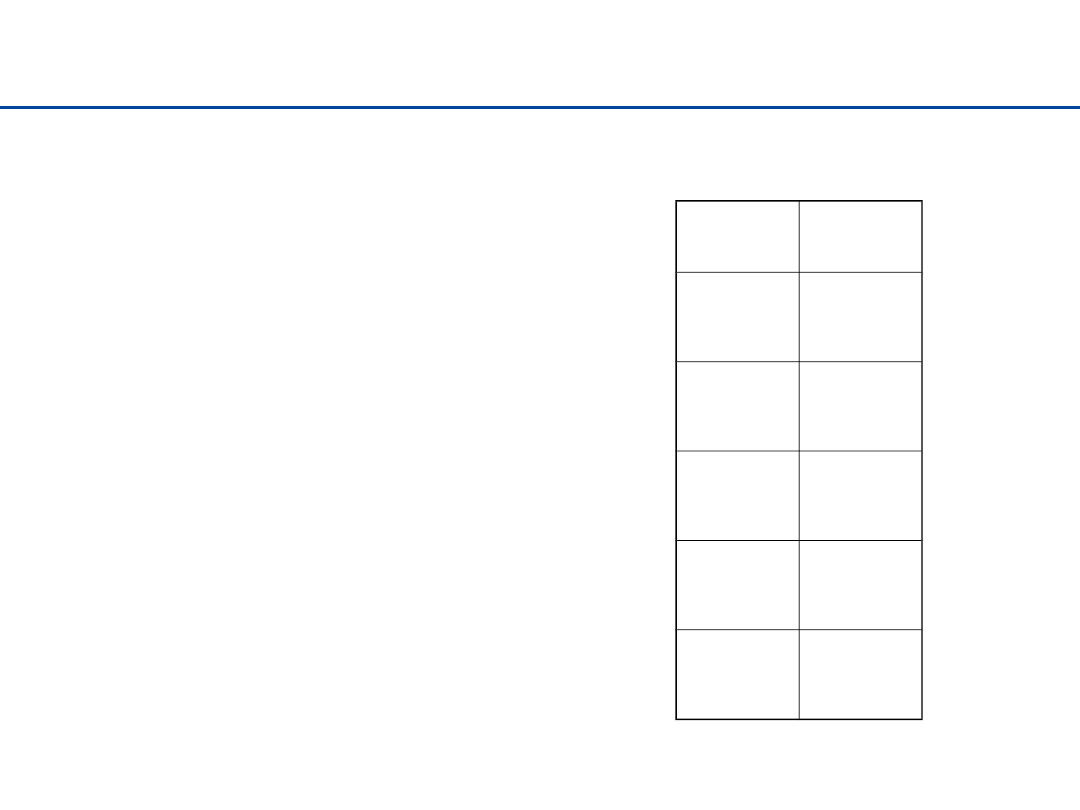
Ilość kroków

 Ilość kroków M(n) potrzebnych

do rozwiązania problemu dla n
dysków spełnia zależność
rekurencyjną

M(1) = 1

M(n) = 2M(n-1) + 1

n

M(n)

1

1

2

3

3

7

4

15

5

31

45

Ilość kroków

 Rozwijając tę zależność dostajemy

M(n)

= 2M(n-1) + 1

= 2*[2*M(n-2)+1] + 1 = 2

2

*

M(n-2) + 1+2

= 2

2

* [2*M(n-3)+1] + 1 + 2

= 2

3

*

M(n-3) + 1+2 + 2

2

=…

 Po k krokach

M(n) = 2

k

*

M(n-k) + 1+2 + 2

2

+ … + 2

n-k-1

 Dla k = n-1

M(n)

= 2

n-1

*

M(1) + 1+2 + 2

2

+ … + 2

n-2

= 1 + 2 + … + 2

n-1

= 2

n

-1

46

Projekt

 Uogólnić zadanie o wieżach Hanoi dla k wież