AISDE - Kolokwium 2 poprawkowe 26 stycznia 2008

Podpis

Zadanie 1 (6p)

Słownik zawiera elementy {1,2,3,4} w BST. Wyszukanie klucza „3” wymaga największej, a „2” najmniejszej złożoności w tym drzewie. Operacja dominująca to porów­nanie kluczy. Narysować BST. Obliczyć złożoność oczeki­waną wyszukiwania klucza k o rozkładzie równomiernym w {1,2,3,4,5}.

BST: 2 / \ 1 4 / 3 Złożoność oczekiwana= 2. (kiedy drzewo jest wyważone.Chyba chodzi o to.

Zadanie 2 (6p)

Słownik upo­rz­ą­d­kowany S zawiera klucze {2, 4,6,8}. Używamy metodę podziału binar­ne­go. Ope­racja dominująca: porównanie kluczy. Ilu operacji wymaga szukanie wszystkich ist­nie­jących kluczy? Ilu operacji wymaga szuka­nie klucza 9? Ilu operacji wymaga wstawianie klucza 3? Jaka jest wysokość drzewa? Dob­r­ać war­to­wników tak, by wyszukiwanie w S al­goryt­mem interpolacyjnym każ­d­e­go istnie­jącego klucza wymagało 1 porów­na­nia.

Dokładamy dwóch wartowników: lower i upper i zgodnie ze str12/wykład 7 drzewo dla k1...k6, gdzie k1 i k6 to wartownicy, a k2, k3, k4, k5 - istniejące klucze. Wyszukanie wszystkich: 2+1+2+3=8operacji Wyszukanie „9”: 3 operacje Wstawienie „3”: 2 operacje Wysokość drzewa=3 interpolacja: Wartownik lewy=0 Wartownik prawy=10

Zadanie 3 (6p)

Wyszukanie wzorca P w tekście T o długości 13 nad alfabetem V={0,1} algorytmem Naive wymagało 49 porównań symboli. Znaleźć wszystkie możliwe pary T, P. n=13.

Kluczem do rozwiązania zadania jest zauważenie, że 49=7*7 i jest to jedyny rozkład tej liczby na czynniki różne od 1 i samej 49. t(n)=(n-m+1)*c = 7*7 tzn: c=7 n-m+1=7 => m=7. c=m => przypadek pesymistyczny. X - dowolny znak z alfabetu V. T=111111111111X P=111111X T=000000000000X P=000000X Jakkolwiek w materiałach wykładowych podane jest, że tekst i wzorzec składają się z identycznych znaków to tak naprawdę nie ma znaczenia jaki jest ostatni znak - trzeba go porównać. A jaki będzie wynik ostatniego porównania - to na złożność nie wpływa. Dr Ogrodzki zgodził się z powyższym rozumowaniem.

Zadanie 4 (6p)

P=[aba], V={a,b}. Określić za pomocą funkcji sufiksowej i wypisać tablicę przejść automatu. Narysować graf automatu. Prefiksy: P0={} P1={a} P2={ab} P3={aba}

q=0 x=.a. q'=sigma(epsa)=1 q=0, x=.b. q'=sigma(epsb)=0 q=.1, x=.a. q'=sigma(ab)=2 q=.1., x=.b. q'=sigma(aa)=1 q=.2, x=.a. q'=sigma(aba)=3 q=.2, x=.b. q'=sigma(abb)=0 q=3., x=.a. q'=sigma(abaa)=1 q=3, x=..b.. q'=sigma(abab)=2 Graf automatu

Zadanie 5 (6p)

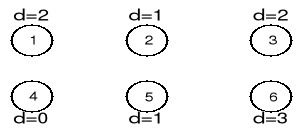
Narysować krawędzie grafu skierowanego acyklicznego o najmniejszej liczbie krawędzi, takiego, że przeszukanie go algo­ryt­mem BFS dało podane wartości d. Ile rozwiązań ma zadanie? Podaj wszystkie. Mamy mieć poza wierzchołkiem startowym V4 trzy warstwy:d=1, d=2, d=3. Dlatego dla każdego rozwiązania muszą istnieć takie krawędzie: V4 - > V2, oraz V4 ->V5. Następnie wierzchołki 1 i 3 mogą być połączone z dowolnym z wierzchołków 2 oraz 5. Natomiast wierzchołek 6 musi mieć krawędź od V1 bądź V3. 2*2*2=8 możliwości

---