Pd 9.11.2009

Zad.1 Oblicz granice jednostronne funkcji f w punkcie
, jeżeli

a)
,
; b)
,
; c)
,
.

Na podstawie obliczonych granic naszkicuj wykresy tych funkcji w sąsiedztwie
.

Zad.2 Obliczyć granice

a)
, b)
, c)
.

Zad.3

Zbadać ciągłość funkcji

a)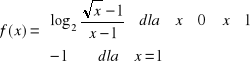
, b)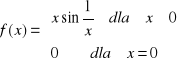

Wskazówka b)

Wykazać, że jeżeli f jest funkcją ograniczoną w otoczeniu punktu
i
, to
.

Porównaj z odpowiednim twierdzeniem dla ciągów.

Zad.4

Czy można tak określić stałe a, b aby funkcja była ciągła

a)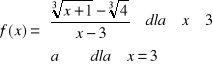

b)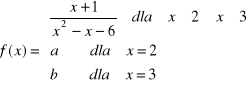

Zad.5

a) Wykazać, że równanie
posiada pierwiastek rzeczywisty w przedziale
.

b) Wykazać, że równanie
ma pierwiastki w przedziałach

.

Wyznaczyć te pierwiastki z dokładnością do 0,5.

Zad.6

Wykazać, że istnieje liczba x leżąca w przedziale
taka, że
.

Odp.

Zad.1

a)
,
, b)

, c)

Zad. 2 a)
, b) nie istnieje, c)

Zad. 3 a) funkcja ciągła. b) funkcja ciągła

zad. 4 a)
b) stałe nie istnieją

Zad.5 b) Pierwiastki
należą do przedziałów
;
.

6