• Dlaczego rachunek podziału wpływa na uproszczenie układu ?

Przy kodowaniu dąży się do znalezienia takich podziałów, aby funkcje przejść automatu zakodowanego zgodnie z tymi podziałami zależały od jak najmniejszej ilości zmiennych.

• Co to jest para podziałów ?

Para podziałów П1 i П 2 stanów wewnętrznych to uporządkowana dwójka podziałów П 1--> П2 taka, że dla każdych dwóch stanów zawartych w pewnym bloku z П 1 i dla każdego xi
X, xi - następniki tych stanów zawarte są w pewnym bloku podziału П 2

• Co to są podziały prawidłowe ?

Podziałami prawidłowymi nazywamy podziały spełniające warunki:

- są to podziały dwublokowe

- liczba elementów każdego bloku 2k - 1

• Etapy kodowania automatów synchronicznych z zastosowaniem rachunku podziałów

- Wyznaczyć zbiór par podziałów gdzie П --> τ gdzie τ jest pewnym podziałem dwublokowym lub w szczególności prawidłowym

- Narysować graf par podziałów

- Zaznaczyć na grafie podziały dogodne ze względu na wyjście

- Wybrać rodzinę Tkopt. o minimalnej cenie

• Co to jest rodzina końcowa T_k i rodzina końcowa optymalna T_kopt ?

Rodziną końcową podziałów Tk nazywamy zbiór podziałów który można przyjąć do kodowania, tzn. zbiór spełniający warunek zerowego iloczynu

Rodziną końcową optymalną Tkopt nazywamy rodzinę końcową Tk wyznaczającą kod dający najprostsze funkcje przejść i wyjść (najprostszy układ)

• Cena podziału wewnętrznego

Ceną podziału wewnętrznego c(τ_i) nazywamy szacunkową ilość zmiennych od których zależy funkcja wzbudzeń przerzutnika Qi zakodowanego zgodnie z τ_i zmniejszoną o 1.

Cenę podziału wewnętrznego wyznacza się z zależności

c(τ_i) = n + l - 1

gdzie

n - liczba zmiennych wejściowych

l - liczba sygnałów Ql od których zależy funkcja wzbudzeń przerzutnika Qi

• Cena sygnału wyjściowego

Dla automatu Moore'a jako cenę sygnału wyjściowego przyjmuje się

c(yi) = l - 1

gdy yi = λ(Q1,..., Ql)

Dla automatu Mealy'ego cena sygnału wyjściowego wzrasta o liczbę zmiennych wejściowych n

c(yi) = n + l - 1

Łączna cena układu uwzględniająca zarówno cenę podziałów jak i cenę wyjść wyraża się wzorem

c = Σc(τ_i) +Σc(yi)

• Czy do kodowania automatów synchronicznych można brać podziały nieprawidłowe ? Jeśli tak to czym to skutkuje ?

Tak, można brać podziały nieprawidłowe ale spowoduje to wzrost liczby elementów z pamięcią użytych do prawidłowego działania naszego automatu.

• Struktura automatu Mealy'ego

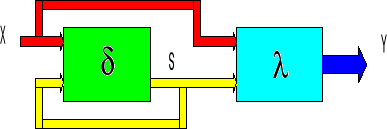
• Struktura automatu Moore`a

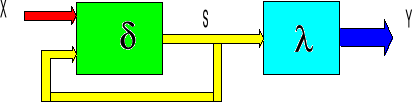
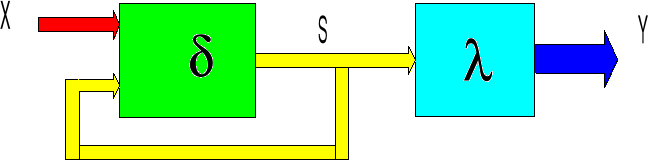
X - alfabet wejściowy (zbiór stanów wejściowych);

S - alfabet wewnętrzny (zbiór stanów wewnętrznych);
Y - alfabet wyjściowy (zbiór stanów wyjściowych);

δ - funkcja przejść δ = f(X,S);

λ - funkcja wyjść dla automatu Mealy'ego λ = f(X,S) dla automatu Moore'a λ = f(S)

• Sposoby opisu automatów

- opis słowny

- wykresy czasowe

- tablica przejść wyjść

- grafy stanów układów

• Warunki jakie musi spełniać zbiór maksymalnych stanów zgodnych Φopt

- każdy stan musi wchodzić co najmniej do jednej grupy (warunek pełności zbioru)

- dla każdej pary każdego zbioru muszą być spełnione wymogi zgodności warunkowej

• Etapy minimalizacji automatu synchronicznego

- zbudowanie tablicy trójkątnej (wpisujemy warunki i wykreślamy wszystkie klatki o sprzecznych wyjściach; klatki niewykreślone, bez względu na zawartość, odpowiadają parom stanów zgodnych

- tworzymy graf relacji zgodności (tworzymy maksymalne grupy stanów zgodnych)

- wyznaczamy zbiór Φ i Φopt

---