Zimny Edyta Woś Aneta Wołowiec Waldemar Wrona Marcin	Podstawy automatyki - laboratorium	Data oddania: 2002-06-24
III MDZ Gr. 1010 Tydzień A 14^15	Wstęp do CODASA. Badanie stabilności układów automatycznej regulacji	Data przyjęcia:

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z podstawowymi elementami automatyki oraz pakietem oprogramowania CODAS-II służącego do symulacji i badania własności dynamicznych zarówno pojedynczych elementów automatyki jak również całych, jednowymiarowych układów automatycznej regulacji (UAR). Celem ćwiczenia jest określenie, dla jakich wartości k układ automatyczny regulacji jest stabilny:

2. Podstawy teoretyczne

Kryterium Nyquista ma duże znaczenie praktyczne, ponieważ pozwala badać stabilność układu zamkniętego na podstawie przebiegu charakterystyki częstotliwościowej układu otwartego, którą to charakterystykę można wyznaczyć doświadczalnie. Opiera się na twierdzeniu, że jeżeli układ regulacji jest stabilny i jego charakterystyka amplitudowo-fazowa G0(jω) dla pulsacji od 0 do +ω nie obejmuje punktu (-1,j0), to wtedy i tylko wtedy po zamknięciu będzie on również stabilny.]

Dobór nastaw regulatorów został przeprowadzony według metody Ziegera-Nicholasa. Metoda ta pozwala uzyskać przebiegi przejściowe z przeregulowaniem około 20% i minimum czasu regulacji tr.

Przyjęte nastawy

dla regulatora.......P: kp=0,5 kpkr

dla regulatora.......PI: kp=0,45 kpkr ; Ti =0,85 Tosc

Przed doborem nastaw regulatorów amplituda oscylacji nie ma charakteru gasnącego dla k>kpkr , natomiast dla k<kpkr amplituda ma charakter gasnący jednakże czas dojścia do wartości ustalonej jest nie do przyjęcia. Aby skrócić czas regulacji dobiera się nastaw regulatorów według metody Ziegera-Nicholasa. Zwraca uwagę zbieżność reguł Ziegera-Nicholasa z wymaganiem zapasu modułu równego 6dB. Zmniejszenie wzmocnienia układu do połowy wzmocnienia krytycznego, przy którym układ znajduje się na granicy stabilności, odpowiada wprowadzenie zapasu modułu dla 6dB.

Transmitancja regulatora

R(s) = K

Dobór regulatora

1. P (proporcjonalny)

2. PI (proporcjonalno całkujący)

3. PID

3. Przebieg ćwiczenia:

G_EW(s); G_OB(s); G_UP(s);

G_R=Kp

1. Kp < K_KR

2. Kp = K_KR

3. Kp > K_KR

Dane:

Stabilny Na granicy stabilności

Niestabilny

G_UP =

G_OB =

G_EW =

Dobrać optymalne nastawy stosując kryterium Nichols Zigler

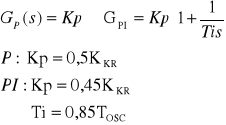
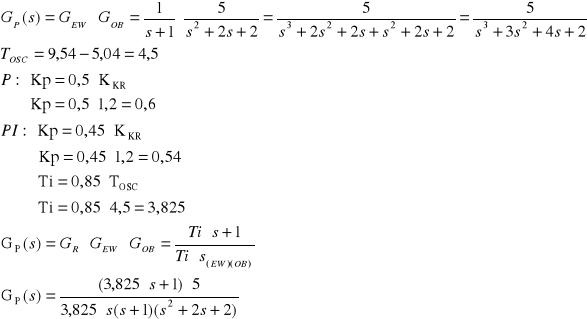
- 3 -

UP

R

EW

X

Y

Obiekt

1

2

3

h(t)

h(t)

h(t)

t

t

t

---