1. Matematyczny opis układu dynamicznego.
   Matematyczny opis układu dynamicznego pozwala na jednoznaczne określenie zachowania się układu, pozwala określić sterowalność i obserwowalność układu. Model opisu może być w postaci macierzowej i różniczkowej:
   POSTAĆ MACIERZOWA:
   X(t)=AX(t)+BU(t) A - macierz stanu
   Y(t)=CX(t) B - macierz wejść
   C - macierz wyjść
   X(t) - zmienne stanu
   POSTAĆ RÓŻNICZKOWA:
   
   
   
   
   

2. Co cechuje układy liniowe? (co musi być spełnione aby układ był liniowy, przykład)
   Układy liniowe to układy dla których obowiązuje zasada superpozycji. Zasada superpozycji - odpowiedź wypadkowa układu na wymuszenie będąca sumą pewnej liczby składowych jest równa sumie odpowiedzi na poszczególne składowe. Układ liniowy musi posiadać następujące równania:
   Równanie algebraiczne liniowe: R₁i+R_Ri=u
   dynamiczne równanie liniowe: L^di(t)/_dt+R*i(t)=u(t)
   Układ liniowy to taki układ w którym sygnały czyli przebiegi wielkości fizycznych rozpatruje się jako funkcje czasu.

3. Co to jest decybel i co oznacza zmiana o 1 dB
   L_m(ω)[dB] = 20 logA(ω)
   Charakterystyka logarytmiczno - amplitudowa przedstawia zależność zmiennej L_m(ω) będącej logarytmem dziesiętnym pulsacji ω.
   Jeżeli 10 log A(ω)=1dB, to
   20 log A(ω)=log 10²⁰ => A=10^1/20≈1,22

4. Co to jest macierz stanu i do czego służy?
   Macierz stanu to macierz A o wymiarach n x n, która występuje w równaniach stanu. Macierz stanu zawiera zmienne stanu: fizykalne, fazowe i kanoniczne. Macierz ta powinna mieć minimalny rozmiar czyli minimalną liczbę zmiennych stanu. Wybrane zmienne stanu muszą spełniać warunek niezależności liniowej. Jeżeli występuje więcej niż jeden zestaw zmiennych stanu to przejście od jednych współrzędnych do innych musi być wzajemnie jednoznaczne. Na podstawie macierzy stanu możemy określić własności dynamiczne danego układu oraz określić stan układu.

5. Co to oznacza, że układ dynamiczny jest stabilny?
   Stabilność układu jest to taka cecha układu, która polega na powracaniu do stanu równowagi stałej po ustaniu działania zakłócenia. Zamknięty układ liniowy będziemy uważać za stabilny jeżeli przy każdej skończonej wartości zakłócenia z(t) i wartości zadanej m(t) dla dowolnych warunków początkowych sygnał wyjściowy dążył będzie do skończonej wartości wstawionej czasu dążącego do nieskończoności. Korzystamy z kryteriów: Hurwitza, Michajłowa, Nygista.

6. Czy charakterystyki statyczne i dynamiczne są tożsame z własnościami układu dynamicznego?
   Charakterystyka statyczna jest jednoznaczna z własnościami statycznymi, natomiast charakterystyka dynamiczna jest jednoznaczna z własnościami dynamicznymi, a własności te określamy za pomocą równań różniczkowych i odpowiadających im transmitancji operatorowych, oraz wykres odpowiedzi y(t) na wymuszenia skokowe.

7. Do czego służą charakterystyczne skokowe?(jakie własności można określić za pomocą)
   Ch. Skokową układu liniowego stacjonarnego nazywamy odpowiedź tego układu na wymuszenie w postaci jednostkowej funkcji skokowej przy zerowych warunkach początkowych. Odpowiedź skokową charakteryzują właściwości dynamiczne elementów i zależy od parametru tego układu oraz czasu t. Ch skokowa może posłużyć do wyznaczania ch-tyk częstotliwościowych. Na podstawie ch-ki skokowej możemy określić z jakim obiektem mamy do czynienia. Dysponując ch skokową możemy określić transmitancję układu wyznaczając jej parametry: współczynnik wzmocnienia k, stała czasową T, czas opóźnienia T₀.
   Do czego służy równanie charakt. det(SI-A)=a_n*Sⁿ + a_n-1*S^n-1 + ...+ a₁*S + a₀
   Równanie charakt pozwala na oceną własności dynamicznych układu. Jeżeli wielomian charakt przyrównamy do zera wyznaczamy miejsca zerowe które są pierwiastkami charakterystycznym równania:
   det(SI-A)=a_n*Sⁿ + a_n-1*S^n-1 + ...+ a₁*S + a₀=0
   det(SI-A)=(S-S­_n)(S-S_n-1)... (S-S₁)

8. Do czego używa się dB w skali logarytmicznej?
   Do opisu logarytmicznych charakterystyk amplitudowych L(ၷ)=20 log M(ω).
   Podziałka osi L(ω) jest liniowa skalowana w dB. Często na tej osi odkłada się bezpośrednio stosunek amplitud M(ω). Podziałka osi M(ω) jest wówczas logarytmiczna.

9. Jak wyznacza się stan układu podać matematyczny opis stanu układu.
   X^(t)=A*X(t) + B*U(t) - równanie stanu.
   Y(t)=C*X(t) - równanie wyjścia X(t) - wektor stanu; U(t) - wektor sygnałów wejściowych; Y(t) - wektor sygnałów wyjściowych; A - macierz stanu; B - macierz wejścia; C - macierz wyjścia.

10. Jaki warunek musi spełniać układ ciągły?
    Zbiór chwil czasowych należy do zbioru chwil rzeczywistych. Jeżeli T=R, gdzie R - to zbiór liczb rzeczywistych, czyli czas jest zmienną ciągłą.

11. Jakie wielkości wyrażamy w dB?
    Podziałka osi L(ω)jest liniowa, skalowana w dB. Często na tej osi odkłada się bezpośredni stosunek amplitud M(ω) podziałka osi M(ω) jest wówczas logarytmiczna. Wartość L(ω) obliczamy wg wzoru: L(ω)=20 log M(ω) i wynik tego obliczenia otrzymuje miano dB. Mnożnik 20 jest umowny. Został wprowadzony aby operować najczęściej wartości L(ω) rzędu od kilku do kilkudziesięciu.

12. Jakie własności układu automatyki można dowieść na podstawie ch. częstotli.
    Podstawą ch. częstotliwościowych jest transmitancja widmowa. Pojęcie transmitancja widmowa odnosi się do układu dynamicznego o następujących właściwościach:
    a. Jednowymiarowy b. Liniowy c. Ciągły d. Stacjonarny e. O stałych skupionych
    
    
    
    
    

13. Narysować schemat blokowy układu opisanego równaniem stanu i równaniem wyjścia i uzasadnić wymiary macierzy A,B,C.
    
    
    
    
    
    
    Dla układów liniowych niestacjonarnych x^(t)=A(t)*x(t) + B(t)*u(t) - równanie stanu - x^(t)=f [x(t),u(t)] ; y(t)=C(t)*x(t) - równanie wyjścia - y(t)=g [ x(t),u(t)]
    A(t) - macierz układu o wymiarach n x n; B(t) - macierz sterowania o wymiarach n x p; C(t) - macierz odpowiedzi o wymiarach q x m. Dla układów stacjonarnych elementy A,B,C są: a. wektor wymuszenia u=u(t)=mac pion[u₁(t),u₂(t),....u_p(t)] - p wymiarowy wektor; b. Wektor odpowiedzi y=y(t)=mac pion [y₁(t)...y_q(t)] - q wymiarowy wektor c. Wektor stanu x=x(t)=mac pion[x₁(t)...x_n(t)] n - wymiarowy wektor.

14. Określ różnice między osiami loczbowymi charakterystyki amplitudowej w skali liniowej i logarytmicznej.
    W skali liniowej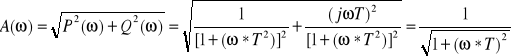
    
    
    W skali logarytmicznej: L_m(ω)=20 log A(ω)= 20 log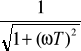
    
    Przedstawiając obie charakterystyki na jednym wykresie wyznaczamy punkt ich przecięcia. Poniżej tego punktu charakterystyka logarytmiczna przyjmuje wartości ujemne, charakterystyka w skali liniowej zaczyna swoje wartości od 1

15. Podać zasady stosowane zmiennych fazowych.
    Zmienne fazowe są jednym z rodzajów zmiennych stanu. Wygodnie jest stosować zmienne fazowe w przypadku, gdy transmitancja układu jest opisana równaniem:
    G(s)=y(s)/u(s)=k/(Sⁿ + a_n-1*S^n-1 + ...+ a₁*S + a₀). Wtedy zmienne stanu tworzy się dobierając jeden z sygnałów układu oraz kolejne pochodne tego sygnału. Przy założeniu że zmienną fazową będzie sygnał wyjściowy i jego pochodne równania wyglądają :
    y(t)->x­₁(t) y²(t)->x₂(t) y^n-1(t)->x_n(t)
    {x₁^{^}(t)=x₂(t)
    {x₂^{^}(t)=x₁(t)
    {....
    {x_n-1^{^}(t)=x_n(t)
    {x_n^{^}(t)=a₀*x₁(t)-a₁x₂(t)-...-a_n-1x₁(t) + ku(t)

16. Reguła Zingera i Nicolsona.
    Jest to reguła doświadczalnego nastawiania regulatorów. Prowadzi do uzyskania przebiegów przejściowych z przeregulowaniem ok. 20% i min. czasu regulacji tr. Nastawianie przeprowadza się już po zainstalowaniu regulatora w układzie. Kolejność postępowania przy stosowaniu tych regół
    a. Należy nastawić regulator na działanie tylko proporcjonalne. Działania człkujące i różniczkujące powinny być wyłączne.
    b. Należy zwiększyć wzmocnienie proporcjonalne kp regulatora, aż do wystąpienia oscylacji niegasnących w układzie.
    c. Na taśmie rejestratora należ zmierzyć okres tych oscylacji a na skali regulatora należy odczytać krytyczne wzmocnienie proporcjonalne (kp)_kr przy który one wystąpiły.
    d. Zależnie od typu regulatora należy przyjąć określone nastawy.

17. Różnica między sygnałem, a informacją.
    Sygnał jest to przebieg wielkości fizycznej, której co najmniej jeden parametr zależy od przesyłanej informacji np.: kształt, amplituda, częstotliwość.
    Informacja zawarta jest w wartościach lub kształcie przebiegu sygnału. Mówimy, że sygnał jest nośnikiem informacji

18. Różnice między sterowaniem a regulacją.
    Sterowanie - jest to celowe oddziaływanie na określony obiekt tak aby osiągnąć pożądane zachowanie obiektu urządzenia lub pożądane cech procesu. Regulacja - to sterowanie w układzie zamkniętym zawierającym węzeł sumacyjny za pomocą którego realizowane jest sprzęzenie zwrotne.

19. Systemy sterowania dla systemów złożonych
    Systemy złożone to struktury sterowania w których wyróżnia się odrębne funkcjonujące części: elementy automatyki, obiekty i systemy np. sys. sterowania procesem technologicznym. Opis działania: komputery za pomocą urządzeń wyjściowych generujących sygnały wejściowe oddziaływują na elementy wykonawcze które oddziaływują na proces. Za pomocą wektorów sygnałów wyjściowych które oddziaływują na elementy kontrolujące stan procesu oraz urządzeń wejściowych komputera PC kontroluje sterowanie procesem.

20. 
    
    
    Układy nieliniowe. Co to jest narysować wykres i zaznaczyć na nim zakres nieliniowości.
    układem nieliniowym jest każdy układ zawierający chociaż jeden element nieliniowy. Elementy i układy nieliniowe opisywane są za pomocą nieliniowych równań różniczkowych, różnicowych lub algebraicznych. Nie obowiązuje ich zasada superpozycji. Układ statyczny nieliniowy: R_i+R₂(i)*i = u; układ dynamiczny nieliniowy; L^di(t)/_dt+R(t)*i(t)=u(t) gdzie R₂ to oporność zależna nieliniowo od prądu, R(t) = r*e^t to współczynnik zależny nieliniowo od czasu
    
    
    
    
    
    
    
    
    

21. Wskaźniki regulacji określane bez charakterystyk częstotliwościowych.
    a. Wskaźniki uchybu ustalonego ε_s=lim_t→0ε(t) ε_s/Y₀(t)*100% określa się przez podanie wartości dopuszczalnej w jednostkach fizycznych; w jednostkach względnych
    b. Czas regulacji t_r ε_r(t)= ε(t)- ε_s przedział czasu od chwili wymuszenia do chwili w której uchyb przejściowy nie przekroczy 5% wartości max
    c. Współczynnik przeregulowania Η iloraz największej wartości uchybu ε_p1 o znaku przeciwnym do znaku ε_p0 i maksymalnej wartości uchybu przejściowego
    ε_p1/ε_p0*100%
    
    
    
    
    

22. Wyjaśnić co to są adapcyjne układy automatyki.
    Układy adapcyjne - układy w których istnieje możliwość automatycznego doboru parametrów i charakterystyk, a nawet możliwa jest rekonfiguracja sprzętowa. Przykładem takiego działania może być włączenie urządzeń rezerwowych w przypadku awarii głównych urządzeń sterujących. Charakterystyki lub parametry urządzenia mogą się samoczynnie dopasować do zmieniających się własności procesów regulowanego i działających zakłóceń. Przystosowanie może nastąpić przez zmianę wartości zadanych parametrów lub struktury układu.

23. Zasady doboru modelu matematycznego.
    - rozpatrujemy dowolny dynamiczny ciągły liniowy lub nieliniowy tj taki który może być opisany równaniem różniczkowym. Istnieją przypadki że równanie różniczkowe lub układ równań różniczkowych można doprowadzić do postaci normalnej czyli do układu równań różniczkowych pierwszego rzędu
    - aby opisać układ dynamiczny ciągły przy pomocy równań rózniczkowych wyróżnia się n - liniowo niezależnych wielkości fizycznych lub abstrakcyjnych x₁(t), x₂(t), x_n(t)
    - w chwili początkowej t= t₀ istnieje stan początkowy reprezentowany przez n liczb t = t₀*x₁(t₀), x₂(t_0­), x_n(t₀)
    - wyróżniamy n liniowo niezależnych wielkości fizycznych nazywanych współczynnikami stanu lub zmiennymi stanu
    - wspólczynniki stanu zapisane są w postaci wektorowej
    - współrzędne stanu zmieniają się w czasie zgodnie z rozwiązaniami n równań różniczkowych

24. Zastosowanie macierzy transmitancji
    W przypadku elementów o wielu wejściach i wyjściach należy określić macierz transmitancji G(s).
    G₁₁(s) G­₁₂(s) ….. G_1m(s)
    G₂₁(s) G₂₂(s) ….. G_2m­(s)
    G_n1(s) G_n2(s) ….. G_nm(s)
    Gdzie G_ix(s) = y_i(s)/x_x(s) dla i= 1, ..., n; i k =1...m;
    TrANSMITANCJE G_ix(s) są równe stosunkowi transformaty i - tej wielkości wyjściowej do transformaty k - tej wielkości wejściowej przy założeniu, że wszystkie pozostałe wielkości wejściowe i warunki początkowe są równe zeru. Pozwala na określenie własności dynamicznych układu.
    
    
    
    

25. Zinterpretować uchyb.
    Uchyb regulacji jest to różnica między sygnałem zadanym a sygnałem wyjściowym

26. Wyjaśnić co oznacza, że układ regulacji jest statyczny albo astatyczny.
    układy w których uchyb ustalony przy zakłóceniu skokowym jest równy zeru niezależnie od amplitudy wymuszeń nazywamy układami astatycznymi. Układy w któwych uchyb ten jest różny od zera i jego wartość zależy od amplitudy wymuszenia nazywamy układami statycznymi.

27. Narysować schemat blokowy układu opisanego równaniem stanu i równaniem wyjścia i wyjaśnić
    
    
    
    
    
    
    równanie stanu - x^(t)=A(t)*x(t) + B(t)*u(t); równanie wyjścia - y(t)=C(t)*x(t)+D(t)*u(t) A(t) - mac stanu o wym n x n; B(t) - mac wejścia o wym n x p; C(t) - mac wyjścia o wym q x n; D(t) - mac transmisji, jest to mac oddziaływania wejścia na wyjścia.

28. 
    
    
    
    
    
    
    
    
    
    
    
    
    
    Podać własności członu całkującego.
    Sygnał wyjścia regulatora u jest wprost proporcjonalny do całki sygnału uchybu ε. Zapewnia astatyczność układu regulacji znacznie ogranicza bądź eliminuje uchyb statyczny ale wydłuża czas regulacji co niekorzystnie wpływa na stabilność układu. Człon całkujący idealny:
    G(s)= ^k/_s - transmitancja operatorowa; y(t)=kx(t) - równanie członu całkującego
    y(t)=kt*1(t)=h(t)
    
    
    
    
    
    Jeżeli na wejściu członu całkującego pojawi się sygnał x(t)=const to sygnał wyjściowy będzie narastał w funkcji czasu liniowo. Współczynnik k nazywamy wzmocnieniem prędkościowym równy jest tgα.
    Człon całkujący rzeczywisty: G(s)=k/s(1+Ts) - transmitancja operatorowa T - stała czasowa. Odpowiedzi skokowe członu całkującego rzecz. a. Impulsowa, b.skokowa
    a. b.

---