Logika matematyczna.

Zad.1. Jaka jest wartość logiczna zdania :

a).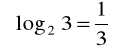



b).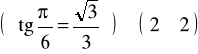

c).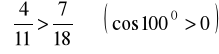
d).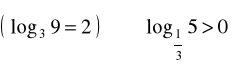

e). ~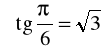
f). ~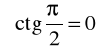
g).
.

Zad. 2. Czy prawdziwe jest zdanie :

a).
jest liczbą nieparzystą dla każdej liczby naturalnej
istnieje liczba naturalna n , dla której
jest liczbą pierwszą )

b).
jest pierwiastkiem równania
)
jest liczbą

pierwszą )

c). ( 2 jest dzielnikiem liczby 15 )
( 15 jest liczbą pierwszą )

d). ( równanie
ma dokładnie jeden pierwiastek )
( równanie
nie ma pierwiastka ) .

Zad.3. Dla jakich wartości logicznych zdań p. i q prawdziwe jest zdanie :

a).
b).

c).
d).

Zad.4. Sprawdzić, czy następujące wyrażenie jest tautologią :

a).
b).

c).
d).

e).
f).

Zad.5. Podane wyrażenia poprzedzić takim kwantyfikatorem, aby otrzymane

zdania były prawdziwe :

.

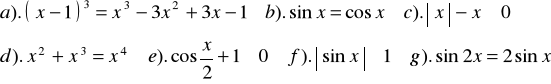
Algebra zbiorów.

Zad.1. Wyznaczyć zbiory
, jeżeli :

.

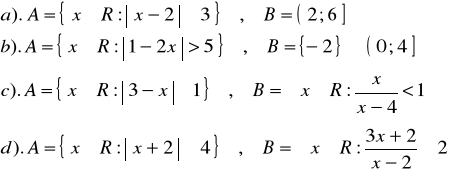
Zad.2. Wyznaczyć zbiory
, jeśli

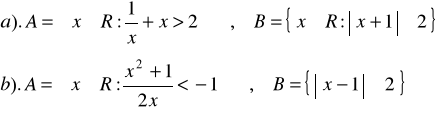
Zad.3. Wyznaczyć
jeżeli :

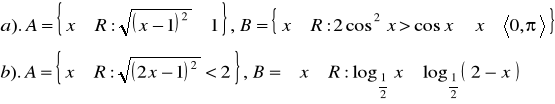
Liczby rzeczywiste.

Zad.1

Oblicz: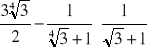
;

Zad.2

Wyznacz p, wiedząc, że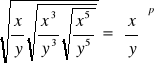
;

Zad.3

Wyznacz te wartości parametru m, dla których równanie

ma nieskończenie wiele rozwiązań.

Zad.4

Udowodnij, że suma sześcianów trzech kolejnych liczb naturalnych jest podzielna przez 9.

Zad.5

Przekształć wyrażenie do prostszej postaci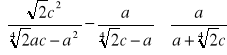

A następnie oblicz jego wartość dla
i
.

Zad.6

Wyznacz liczby naturalne A, B, C tak, aby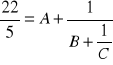
;

Zad.7

Niech a i b będą liczbami całkowitymi. Udowodnij, że
jest kwadratem liczby naturalnej.

Zad.8

Ze zbioru rozwiązań nierówności
wybierz te liczby. Które przydzieleniu przez 3 dają resztę 1.

Zad.9

Przekształć wyrażenie
do prostszej postaci, a następnie oblicz jego wartość dla
i
.

Zad.10

Przekształć wyrażenie
do prostszej postaci, a następnie oblicz jego wartość dla
i
.

Funkcja liniowa.

Zad.1. Sporządzić wykresy funkcji :

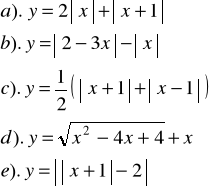
Zad.2. Rozwiązać równania :

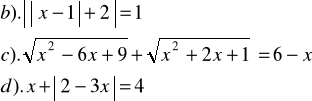
Zad.3. Określić, dla jakich wartości parametru
równanie ma dokładnie jedno

rozwiązanie, dla jakich nie ma rozwiązań, a dla jakich jest tożsamością.

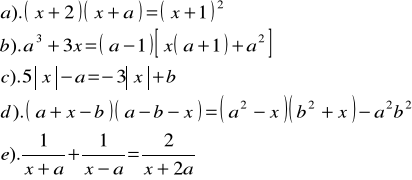
Zad.4. Rozwiązać układ równań o niewiadomych x i y .

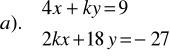
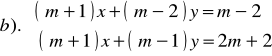
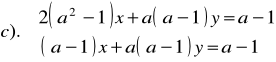
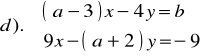
e).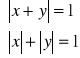

Zad.5. Dla jakich wartości parametru
współrzędne wszystkich punktów

trójkąta o wierzchołkach A ( 0,0 ) , B ( 0,4 ) i C ( 1,0 ) spełniają

nierówność :

Zad.6. Dla jakich liczb naturalnych jest spełniona nierówność :-

Zad.7. Rozwiązać nierówność :

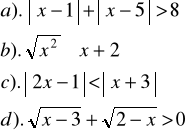
Zad.8. Rozwiązać układ nierówności :

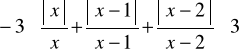
Zad.9. Podać graficzne rozwiązanie nierówności :

Zad.10. Dla jakich wartości parametru
rozwiązanie układu równań

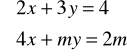
spełnia warunki :
i
?

Zad.11. Dla jakich wartości
punkt przecięcia się prostych danych

równaniami :
i
należy do kwadratu

o wierzchołkach
i
?

Zad.12. Dla jakich wartości parametru
funkcja

jest : a). rosnąca b). malejąca c). stała ?

Zad.13. Napisać równanie prostej przechodzącej przez punkt

i równoległej do prostej
.

Zad.14. Napisać równanie prostej przechodzącej przez punkt

i tworzącej z osią OX kąt
.

Zad.15. Na płaszczyźnie w prostokątnym układzie XOY wyznacz punkty,

których współrzędne spełniają układ nierówności :

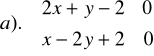
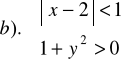
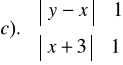
Zad.16. Suma trzech liczb jest równa 210. Jakie to liczby, jeżeli wiadomo,

że druga stanowi
pierwszej, a trzecia jest połową sumy pierwszej

i drugiej liczby.

Zad.17. Kilku przyjaciół postanowiło kupić żaglówkę. Jeżeli każdy z nich da

7 tys. zł, to będzie o 3 tys. za mało, jeżeli natomiast każdy da 8 tys. zł,

to będzie o 4 tys. zł , za dużo. Ilu było przyjaciół oraz jaka jest cena

żaglówki ?

---