1. Wprowadzenie do techniki regulacji
Różnice wynikające ze sterowania w układzie otwartym i zamkniętym rozpatrzmy na przykładzie sterowania silnika obcowzbudnego prądu stałego. Analizę tego układu przeprowadzono przy założeniu, że dynamikę silnika obcowzbudnego prądu stałego można,
z dobrym przybliżeniem, opisać za pomocą równania różniczkowego pierwszego rzędu.
Na rys.1 przedstawiono uproszczony schemat silnika obcowzbudnego prądu stałego.
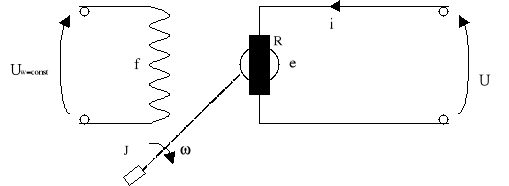
Rys. 1 Uproszczony schemat obcowzbudnego silnika prądu stałego
W układzie tym sterujemy prędkością kątowa *(t) za pomocą napięcia twornika U(t). Zależność wiążącą te wielkości można wyznaczyć korzystając z równań opisujących obwód elektryczny i mechaniczny maszyny.
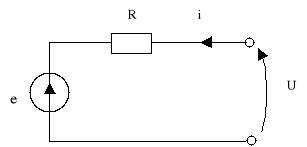
Rys. 2 Schemat obwodu elektrycznego twornika
Na rys. 2 przedstawiono schemat obwodu elektrycznego twornika uwzględniający oporność R twornika oraz siłę elektromotoryczną indukcji e. Siła elektromotoryczna jest równa:
![]()
(1.1)
gdzie c - stała konstrukcyjna maszyny,
φ - strumień wzbudzenia,
ω - prędkość obrotowa silnika.
Ponieważ napięcie Uw w obwodzie wzbudzenia jest stałe, stały jest także strumień wzbudzenia φ . Możemy zatem napisać:
![]()
(1.2)
gdzie ke - stała elektromechaniczna maszyny
Stosując prawo Kirchhoffa do obwodu twornika otrzymujemy równanie:
![]()
(1.3)
Równanie równowagi momentów na wale silnika ma postać:
![]()
![]()
![]()
(1.4)
gdzie: J - całkowity moment bezwładności,
Me - moment elektromagnetyczny silnika,
M - moment obciążenia
Zachodzi także zależność (1.5)
![]()
(1.5)
gdzie: km - stała mechaniczna
Wobec tego podstawiając do równania (1.4) zależności (1.3) i (1.5) otrzymujemy równanie dynamiki silnika:
![]()
(1.6)
oraz
![]()
(1.7)
gdzie: ![]()
- stała czasowa obiektu,
R - rezystancja twornika,
![]()
; ![]()
- wzmocnienia statyczne.
W układzie tym sterujemy prędkością kątową *(t) za pomocą napięcia twornika U(t), przy występowaniu zakłócenia w postaci obciążenia M(t).
Przedstawiając równanie (1.7), za pomocą schematu blokowego, otrzymujemy schemat sterowania silnika w układzie otwartym (w otwartej pętli sprzężenia zwrotnego).
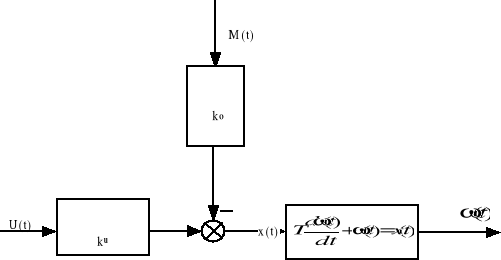
Rys. 3. Schemat blokowy sterowania silnika w otwartej pętli
Celem sterowania jest umożliwienie pracy silnika ze stałą, określoną prędkością *zad(t). Przeanalizujmy pracę silnika w układzie otwartym. W pierwszym etapie analizy przyjmijmy, że znana jest dokładnie dynamika układu. Dla napięcia zasilania U(t)=U0, rozpatrzmy dwa przypadki:
moment obciążenia jest równy zero,
moment obciążenia jest równy M(t)=M0.
W pierwszym przypadku równanie dynamiki silnika przyjmuje postać:
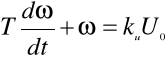
. (1.8)
Przy zerowych warunkach początkowych (tzn., gdy silnik startuje z prędkością *(0)=0), rozwiązanie równania różniczkowego (1.8) jest następujące (1.9):
![]()
. (1.9)
Dla przykładowych danych: T=2, U0=12, ku=2 przebieg *(t), przedstawia rys. 4.
Rys. 4. Przebieg prędkości kątowej silnika obcowzbudnego w układzie otwartym
Wartość prędkości kątowej w stanie ustalonym (dla t->*) równa się ![]()
. Stąd wynika, że aby silnik pracował z zadaną prędkością (![]()
=![]()
), należy go zasilać napięciem równym: ![]()
.
Sterowanie takiego układu wydaje się bardzo proste. W analizie tego przypadku poczyniliśmy jednak założenie, że moment obciążenia jest równy zero. Prędkość w biegu jałowym jest inna niż przy obciążeniu. Należy zatem przeanalizować sytuację, w której moment obciążenia będzie różny od zera. W tej sytuacji dynamika układu opisana jest równaniem (1.7),
a rozwiązanie tego równania (przy zerowych warunkach początkowych) jest następujące:
![]()
. (1.10)
Ten przypadek, przy założeniu wartości momentu obciążenia M(t)=M0=6, oraz wzmocnienia k0=1, przedstawia rys. 5.
Rys. 5. Przebieg prędkości kątowej silnika obcowzbudnego, w układzie otwartym, w przypadku uwzględnienia stałego momentu obciążenia
Wartość prędkości kątowej w stanie ustalonym, przy działaniu stałego obciążenia, można wyznaczyć z równania (1.4):
![]()
.
Błąd pomiędzy wartością zadaną a uzyskaną prędkością, w tym przypadku, wynosi:
![]()
.
Im większe obciążenie, tym wartość prędkości kątowej silnika w układzie otwartym jest mniejsza (bardziej różni się od wartości zadanej).
Analiza przeprowadzona w dwóch poprzednich przypadkach dotyczyła sterowania silnika
o znanej charakterystyce dynamicznej. Dynamika silnika zależy od wielu czynników i może się zmieniać w trakcie długiej eksploatacji maszyny (np. starzenie się elementów konstrukcyjnych). Przeprowadźmy analizę w przypadku, w którym wartość stałej elektromechanicznej ke różni się od wartości wyznaczonej na początku. Załóżmy nową wartość stałej jako: ![]()
. Wtedy wartość stałej czasowej ![]()
, a wzmocnienia statyczne przyjmują wartości ![]()
oraz ![]()
.
Przebieg charakterystyki dynamicznej silnika, przy uwzględnieniu nowych wartości parametrów w równaniu (1.2), przedstawia rys. 6.
Rys. 6. Przebieg prędkości kątowej silnika obcowzbudnego, w układzie otwartym, w przypadku zmiany właściwości dynamicznych silnika
Ustalona wartość prędkości kątowej w tym przypadku równa jest:
![]()
.
Nasza wiedza o maszynie i środowisku, w którym pracuje nie jest doskonała. Zakłócenia wynikające ze zmiany obciążenia, czy też zmiany parametrów maszyny są nierozerwalnie zwiazane z jej pracą. Jak można zauważyć sterowanie w układzie otwartym, przy występowaniu zakłóceń, nie daje zadowalających rezultatów.
Biorąc to wszystko pod uwagę, rozpatrzmy sterowanie silnika w układzie zamkniętym (układzie ze sprzężeniem zwrotnym - rys. 7).
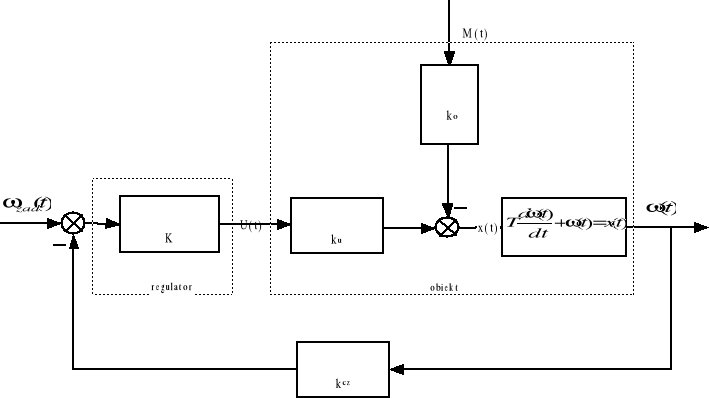
Rys. 7. Schemat blokowy sterowania silnika w zamkniętej pętli sprzężenia zwrotnego
W układzie tym mierzymy wartość prędkości kątowej *(t) (za pomocą tachometru)
i porównujemy (odejmujemy) w węźle sumacyjnym z wartością zadaną *zad(t). W celu otrzymania aktualnej wartości napięcia zasilającego silnik, sygnał błędu jest wzmacniany, przez wzmocnienie regulatora proporcjonalnego Kp. Porównanie prędkości najczęściej realizowane jest w woltach, ze względu na możliwość zastosowania liniowego przetwornika pomiarowego prędkość-napięcie. Wzmocnienie przetwornika określono na schemacie symbolem kcz. Zastosowany w analizie regulator proporcjonalny jest najprostszym elementem regulatora klasycznego PID. Zastosowano go w celu uproszczenia analizy układu.
Zatem równanie dynamiki silnika w układzie z rys. 7 przyjmuje postać:
![]()
, (1.11)
a rozwiązanie tego równania:
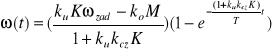
. (1.12)
Przeprowadźmy analogiczne rozważania, jak dla układu otwartego. Rozpatrzmy najpierw przypadek, w którym moment obciążenia jest równy zero. Prędkość kątowa wyznaczona dla zerowego momentu obciążenia jest następująca:
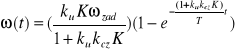
. (1.13)
Przebieg prędkość kątowej, dla przyjętych wartości kcz=1, K=5 oraz *zad=24, przedstawiono na rys. 8.
Rys. 8. Przebieg prędkości kątowej, w układzie zamkniętym, przy zerowym obciążeniu
Wartość prędkości kątowej w stanie ustalonym, dla zerowego obciążenia, można wyznaczyć
z zależności:
![]()
. (1.14)
Dla przyjętych w analizie wartości parametrów, prędkość kątowa w stanie ustalonym przyjmuje wartość *ust=21,82.
Uwzględniając obciążenie różne od zera M(t)=M0, otrzymujemy zależność określającą prędkość kątową, za pomocą równania (1.6). Przebieg prędkości kątowej w tym przypadku przedstawiono na rys. 9.
Rys. 9. Przebieg prędkości kątowej w układzie zamkniętym z uwzględnieniem obciążenia
Wartość prędkości kątowej w stanie ustalonym, przy działaniu stałego obciążenia, można wyznaczyć z zależności:
![]()
. (1.15)
Dla przyjętych w analizie wartości parametrów, prędkość kątowa w stanie ustalonym przyjmuje wartość *ust=21,27.
W przypadku trzecim założono inne wartości parametrów maszyny od wcześniej zidentyfikowanych. Analogicznie, jak dla układu otwartego, wartość stałej czasowej ![]()
, wzmocnienia statyczne: ![]()
oraz ![]()
.
Rys. 10. Przebieg prędkości kątowej, w układzie zamkniętym, w przypadku zmiany właściwości dynamicznych silnika
Wartość prędkości kątowej w stanie ustalonym, dla zerowego obciążenia, można wyznaczyć
z zależności:
![]()
(1.16)
Dla przyjętych w analizie wartości parametrów, prędkość kątowa w stanie ustalonym przyjmuje wartość *ust=21,43. Jak można zauważyć dla wszystkich rozpatrywanych przypadków sterowania w układzie zamkniętym, w odróżnieniu od sterowania w układzie otwartym, wartości prędkości kątowej były zbliżone i nieznacznie różniły się od wartości zadanej.
Podsumowanie
Wnioski wynikające z analizy rozpatrywanego przykładu są następujące:
stosowanie układu zamkniętego przeciwdziałała wpływowi zakłóceń, działających na obiekt regulacji,
dynamika (określona przez stałą czasową układu) w układzie zamkniętym jest dużo lepsza niż w układzie otwartym,
w przypadku zastosowania bardziej złożonej struktury regulatora, błąd regulacji można sprowadzić do zera.
W omawianym przykładzie działanie układu regulacji zostało przedstawione w sposób poglądowy. W celu precyzyjnego wyjaśnienia istoty działania układów regulacji, analizy
i syntezy tych układów, w kolejnych rozdziałach, zostaną przedstawione podstawy teorii regulacji.
Teoria regulacji jest obszerną dziedziną nauki o sterowaniu w układach ze sprzężeniem zwrotnym. Do głównych zadań teorii regulacji należą:
metody opisu właściwości dynamicznych elementów automatyki,
metody identyfikacji obiektów sterowania,
stabilność układów automatyki,
projektowanie układów regulacji,
metody analizy i korekcji układów regulacji.
Przykład wprowadzający zaczerpnięto z podręcznika: Kaula R.: Podstawy automatyki. Wydawnictwo Politechniki Śląskiej, Gliwice 2005.
2
Podstawy automatyki
3
1. Wprowadzenie do techniki regulacji
Wyszukiwarka
Podobne podstrony:
Wyznaczanie stałej siatki dyfrakcyjnej, Prz inf 2013, I Semestr Informatyka, Fizyka, SPRAWOZDANIA DU
SiS strona tytulowa spr, Prz inf 2013, I Semestr Informatyka, Fizyka, Wykłady-Fizyka, Sygnały i Syst
Tabela pomiarowa, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laboratorium stare
tabele 1B+, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laboratorium stare, 1b
ćw 23, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laboratorium stare, Fizyka Dam
Ćwiczenie nr 44 prawie dobre ale juz teraz lux, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA
ćw 1 obliczenia, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laboratorium stare,
spr5, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laboratorium stare, bartochowsk
obliczenia ćw23, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laboratorium stare,
Ćwiczenie nr 44, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laboratorium stare,
Wstęp teoretyczny ćw 44, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laboratorium
pierwsza strona sprawozdania własne, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki,
pierwsza strona sprawozdania, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laborat
Ćwiczenie 47, Prz inf 2013, I Semestr Informatyka, Fizyka, SPRAWOZDANIA DUZO, laboratorium
sprawko1bwstę pteoretyczny, Prz inf 2013, I Semestr Informatyka, Fizyka, [FIZYKA] Laborki, laborator
więcej podobnych podstron