Wydział ISiE
Kierunek IS (wieczorowo)
Semestr 1
Grupa 2
Sekcja 2:
Aleksandra Samela
Arkadiusz Kurek
Krzysztof Grabkowski
BADANIE DRGAŃ RELAKSACYJNYCH
Wstęp teoretyczny
Drgania - pojęcie to jest bardzo często stosowane w fizyce - są to okresowe lub prawie okresowe zmiany stanu układu fizycznego ( np. wahadła, struny, obwodu elektrycznego ), zachodzące dokoła pewnego położenia równowagi pod wpływem dostarczonej do układu energii. Czas potrzebny do wykonania jednego cyklu drgania nazywamy okresem drgań.
Drgania dzielimy na:
harmoniczne
tłumione
wymuszone
samowzbudne.
Z drganiami samowzbudnymi bardzo często możemy spotkać się w przyrodzie przykładem może być tutaj praca serca. W każdym układzie wytwarzającym drgania samowzbudne wyróżniamy: źródło energii, regulator dopływu energii do układu drgającego oraz układ drgający. Regulator i układ drgający kierują nawzajem swoją pracą. Samowzbudny układ drgający zdolny jest do wytworzenia drgań nie zanikających. Warunkiem energetycznym powstawania takich drgań jest równość energii dostarczanej ze źródła i wydatkowanej przez układ w ciągu każdego okresu.
Drgania samowzbudne relaksacyjne mają przebieg okresowy różny od sinusoidalnego, nie zanikający mimo istnienia oporów.
Drgania relaksacyjne są drganiami samowzbudnymi i charakteryzują się tym, że część energii zgromadzonej w tzw. akumulatorze rozprasza się w postaci ciepła. Mogą one zachodzić jedynie w układach nieliniowych. Wygaśnięcie tych drgań równoważne jest odcięciu dopływu energii. W każdym okresie mamy do czynienia z powolnym ładowaniem akumulatora i szybkim jego wyładowaniem.
Elektryczne drgania relaksacyjne powstają w obwodzie z elementem nieliniowym, którym może być lampa gazowa, dioda tunelowa, dioda Zenera. W naszym ćwiczeniu będziemy wykorzystywać lampę gazową.
Lampa jarzeniowa - jest to lampa dwuelektrodowa wypełniona gazem szlachetnym (argon, neon) pod niewielkim ciśnieniem. Katody niklowe lub molibdenowe są aktywowane cezem, sodem, lub potasem. Po przyłożeniu do elektrod napięcia zaczyna płynąć niewielki prąd, ponieważ w bańce zawsze znajduje się niewielka liczba jonów, powstałych np. pod działaniem promieni kosmicznych. Przy odpowiednio dużym natężeniu pola elektrycznego przyspieszone elektrony zaczynają jonizować gaz cząsteczki gazu. Dodatnie jony przyspieszone polem elektrycznym bombardują powierzchnię katody powodując powstanie nowych elektronów. Elektrony te dążąc do anody jonizują cząsteczki gazu. Zachodzi więc proces, w którym katoda otrzymuje więcej jonów dodatnich, niż emituje elektronów. Jony te mają małą ruchliwość i wokół katody tworzy się obszar ładunku przestrzennego przyspieszającego elektrony. Dochodzi do wyładowania lawinowego i przez gaz płynie znaczny prąd. Procesowi temu towarzyszy wzbudzanie atomów gazu co z kolei prowadzi do świecenia katody. Wielkość obszaru świecącego w pobliżu katody zależy od natężenia prądu, a gęstość prądu pozostaje stała. W pobliżu katody mamy do czynienia z dużym spadkiem potencjału (spadek katodowy), między obłokiem dodatnich jonów i katodą.
Napięcie niezbędne do zainicjowania wyładowania samoistnego nazywa się napięciem zapłonu UZ. Wartość ta zależy od gazu wypełniającego lampę i rodzaju materiału katody. Wyładowanie jarzeniowe może być przerwane dopiero po obniżeniu napięcia do napięcia gaśnięcia Ug , niższego od napięcia zapłonu.
Elektryczny obwód RC
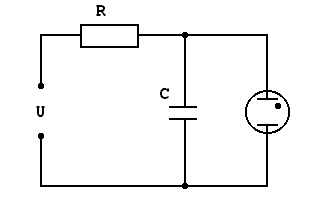
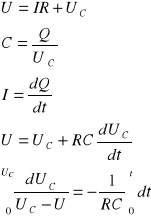
Równanie zmian napięcia podczas ładowania kondensatora:
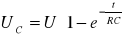
RC - stała czasowa układu
Gdy spadek napięcia na kondensatorze ( na lampie również ) wzrośnie do napięcia zapłonu, wówczas przez lampę zacznie płynąć prąd, co spowoduje rozładowywanie się kondensatora do napięcia gaśnięcia. Po rozładowaniu, lampa nie przewodzi prądu, a cały cykl zacznie się powtarzać.
Czas ładowania kondensatora do napięcia zapłonu wynosi: 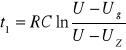
Czas rozładowania kondensatora do napięcia gaśnięcia wynosi: 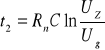
Rn - rezystancja lampy gazowej w czasie przewodzenia
Okres drgań relaksacyjnych jest sumą czasu ładowania i rozładowania T = t1 + t2.
Lecz w ogólnym wzorze pomijamy czas rozładowania, gdyż jest on znacznie mniejszy od czasu ładowania, wówczas wzór na okres drgań relaksacyjnych wynosi: 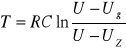
.
Układ Pomiarowy
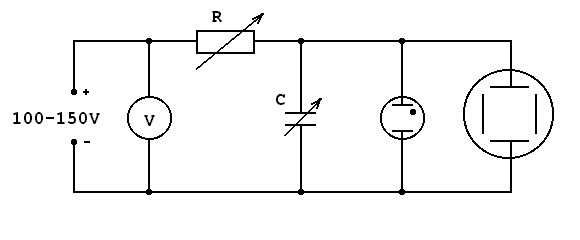
UZ = ( 92,6 ± 0,2 ) V - napięcie zapłonu
Ug = ( 75,8 ± 0,2 ) V - napięcie gaśnięcia neonówki.
3. Badanie zależności okresu drgań od rezystancji.
Przy ustalonym napięciu zasilającym i ustalonej pojemności mierzymy okres drgań relaksacyjnych:
dla okresu T > 0,5 s mierzymy stoperem czas N ( N = 10 ) okresów:
![]()
UZ = ( 92,6 ± 0,2 ) V - napięcie zapłonu
Ug = ( 75,8 ± 0,2 ) V - napięcie gaśnięcia neonówki.
Pomiary wykonujemy dla wartości rezystancji R w granicach 500 - 1700 kΩ co 200 kΩ
Tabela pomiarowa 1
U = 120 [V]
R [kΩ] |
C1= 3 μF |
C2= 6 μF |
||
|
t [s] |
T [s] |
t [s] |
T [s] |
500 |
3,7 |
0,37 |
14,3 |
1,43 |
700 |
5,4 |
0,54 |
19,9 |
1,99 |
900 |
7,3 |
0,73 |
25,2 |
2,52 |
1100 |
8,3 |
0,83 |
29,4 |
2,94 |
1300 |
9,6 |
0,96 |
35,4 |
3,54 |
1500 |
11 |
1,1 |
41,5 |
4,15 |
1700 |
13 |
1,3 |
43,8 |
4,38 |
Metodą regresji liniowej obliczamy nachylenie charakterystyki:
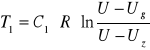
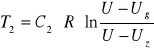
T500 = 0,72 ± 0,03 T500= 1,44 ± 0,06
T700 = 1,01 ± 0,04 T700= 2,02 ± 0,08
T900 = 1,30 ± 0,05 T900= 2,60 ± 0,11
T1100 = 1,58 ± 0,07 T1100= 3,17 ± 0,13
T1300 = 1,87 ± 0,08 T1300= 3,74 ± 0,16
T1500 = 2,16 ± 0,09 T1500= 4,32 ± 0,18
T1700 = 2,5 ± 0,1 T1700= 4,90 ± 0,2
Tsr = 1,59 ± 0,07 Tsr = 1,85 ± 0,13
4. Badanie zależności okresu drgań od pojemności.
Przy ustalonym napięciu zasilającym i ustalonej rezystancji R mierzymy okres drgań relaksacyjnych dla różnych wartości pojemności C w zakresie 1 μF do 10 μF
UZ = ( 92,6 ± 0,2 ) V - napięcie zapłonu
Ug = ( 75,8 ± 0,2 ) V - napięcie gaśnięcia neonówki.
Tabela pomiarowa 2
U = 120 [V]
C [μF] |
R1 = 1100 [kΩ] |
R2 = 1500 [kΩ] |
||
|
t [s] |
T [s] |
t [s] |
T [s] |
1 |
6,2 |
0,62 |
6,4 |
0,64 |
2 |
10,4 |
1,04 |
13,7 |
1,37 |
3 |
9,5 |
0,95 |
12,2 |
1,22 |
4 |
14 |
1,4 |
18,1 |
1,81 |
5 |
21,2 |
2,12 |
27,8 |
2,78 |
6 |
30,2 |
3,02 |
39,9 |
3,99 |
7 |
33,8 |
3,38 |
49,3 |
4,93 |
8 |
41,5 |
4,15 |
55 |
5,5 |
9 |
41 |
4,1 |
57 |
5,7 |
10 |
46,2 |
4,62 |
62 |
6,2 |
Metodą regresji liniowej obliczamy nachylenie charakterystyki:
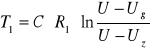
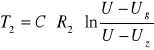
T1 = 0,53 ± 0,02 T1 = 0,72 ± 0,03
T2 = 1,06 ± 0,04 T2 = 1,44 ± 0,06
T3 = 1,58 ± 0,07 T3 = 2,16 ± 0,09
T4 = 2,11 ± 0,9 T4 = 2,88 ± 0,12
T5 = 2,64 ± 0,11 T5 = 3,60 ± 0,15
T6 = 3,17 ± 0,13 T6 = 4,32 ± 0,18
T7 = 3,70 ± 0,15 T7 = 5,04 ± 0,21
T8 = 4,22 ± 0,18 T8 = 5,76 ± 0,24
T9 = 4,75 ± 0,2 T9 = 5,48 ± 0,27
T10 = 5,28 ± 0,22 T10 = 7,2 ± 0,3
Tsr = 2,9 ± 0,12 Tsr = 3,96 ± 0,17Wnioski końcowe.
Z przeprowadzonego badania zależności okresu drgań T od rezystancji R, przy dwóch różnych pojemnościach kondensatora C i stałym napięciu zasilającym uzyskaliśmy następujące wyniki:
podczas wzrostu rezystancji R w granicach od 500 do 1700 kΩ co 200 kΩ okres drgań wzrastał proporcjonalnie wraz ze wzrostem rezystancji, przy różnych pojemnościach kondensatorów C.
okres drgań w układzie z kondensatorem o większej pojemności jest znacznie większy od okresu w układzie z mniejszą pojemnością kondensatora C.
Przy badaniu zależności okresu drgań od pojemności C, przy stałym napięciu 120 V i stałej rezystancji 1100 kΩ i 1500 kΩ, zmieniając pojemność kondensatora C w zakresie od 1 μF do 10 μF otrzymaliśmy następujące wyniki, że wraz ze wzrostem pojemności C wzrastał proporcjonalnie okres drgań T. Okres drgań w układzie z większą rezystancją jest znacznie większy od okresu w układzie z mniejszą rezystancją.
Okres drgań relaksacyjnych zależy od stałej czasowej oraz od przyłożonego napięcia zasilającego. Okres jest tym mniejszy, im stała czasowa RC przyjmuje mniejsze wartości.
-1-
Wyszukiwarka
Podobne podstrony:
9623616767 Concord 7510 HMMWV Workhorse of the US Army
7510
praca-magisterska-wa-c-7510, Dokumenty(2)
7510
7510
7510
7510
7510
9623616767 Concord 7510 HMMWV Workhorse of the US Army
9623616767 Concord 7510 HMMWV Workhorse of the US Army
7510
praca magisterska 7510
7510 Wodzimierz Puchalski
ROOT DO SAMSUNGA GT B 7510
więcej podobnych podstron