Sprawozdanie z ćwiczenia 57

„Zależność oporu elektrycznego metalu i półprzewodnika od temperatury”

Celem ćwiczenia jest zbadanie zależności oporu elektrycznego metalu i półprzewodnika od temperatury.

POMIARY

Temperatura [°C]	Opór [kΩ] Grzanie | Chłodzenie
	Omomierz 1		Omomierz 2		Omomierz 3
25±0,1	0,157±0,001	0,156±0,001	0,224±0,001	0,255±0,001	0,623±0,001	0,623±0,001
30±0,1	0,128±0,001	0,131±0,001	0,228±0,001	0,229±0,001	0,623±0,001	0,623±0,001
35±0,1	0,104±0,001	0,110±0,001	0,232±0,001	0,233±0,001	0,623±0,001	0,623±0,001
40±0,1	0,088±0,001	0,093±0,001	0,236±0,001	0,236±0,001	0,623±0,001	0,623±0,001
45±0,1	0,075±0,001	0,079±0,001	0,239±0,001	0,240±0,001	0,623±0,001	0,623±0,001
50±0,1	0,063±0,001	0,067±0,001	0,243±0,001	0,244±0,001	0,623±0,001	0,623±0,001
55±0,1	0,054±0,001	0,057±0,001	0,247±0,001	0,248±0,001	0,623±0,001	0,623±0,001
60±0,1	0,046±0,001	0,049±0,001	0,251±0,001	0,251±0,001	0,623±0,001	0,623±0,001
65±0,1	0,038±0,001	0,042±0,001	0,255±0,001	0,255±0,001	0,623±0,001	0,623±0,001
70±0,1	0,034±0,001	0,036±0,001	0,258±0,001	0,259±0,001	0,623±0,001	0,623±0,001
75±0,1	0,029±0,001	0,031±0,001	0,261±0,001	0,263±0,001	0,622±0,001	0,623±0,001
80±0,1	0,025±0,001	0,027±0,001	0,266±0,001	0,267±0,001	0,622±0,001	0,622±0,001
85±0,1	0,022±0,001	0,023±0,001	0,269±0,001	0,270±0,001	0,622±0,001	0,622±0,001
90±0,1	0,019±0,001	0,020±0,001	0,273±0,001	0,274±0,001	0,622±0,001	0,622±0,001
95±0,1	0,017±0,001	0,018±0,001	0,277±0,001	0,278±0,001	0,622±0,001	0,622±0,001
100±0,1	0,015±0,001		0,281±0,001		0,622±0,001	0,622±0,001

WSTĘP TEORETYCZNY

Opór elektryczny

Jest to stosunek napięcia do natężenia prądu.

R [Ω] - opór elektryczny [om]

Dla przewodników spełniających prawo Ohma opór elektryczny jest stały.

R = const

Mechanizmy przewodnictwa elektrycznego w ciałach stałych

Elektrony w przewodnikach metalicznych poruszają się w ciągłym swobodnym ruchu. Natrafiając na przeszkodę zmieniają swój kierunek i prędkość. Główną rolę w przewodnictwie zajmują elektrony walencyjne. Występują dwa podstawowe pasma:

pasmo walencyjne - zakres energii jaką posiadają elektrony walencyjne związane z jądrem atomu, oraz pasmo przewodnictwa - zakres energii jaką posiadają elektrony walencyjne uwolnione z atomu, będące wówczas nośnikami swobodnymi w ciele stałym.

Żeby w danym materiale mógł płynąć prąd elektryczny muszą istnieć swobodne nośniki, pojawiają się one wtedy gdy elektrony przenoszą się z pasma walencyjnego na pasmo przewodnictwa.

Zależność przewodnictwa elektrycznego metali od temperatury.

Ze zmianą temperatury szybkość poruszających się elektronów zmienia się. Jony oddziałują ze sobą siłami elektrycznymi, dlatego drgają jednocześnie wszystkie jony w sieci. Drgania jonów nie zanikają w temperaturze zera bezwzględnego, lecz drgają z tak zwaną energia zerową. Drgające jony stanowią przeszkodę dla poruszających się elektronów. Przeszkoda ta wzrasta razem ze wzrostem amplitudy drgań, przez co elektron zderzając się z nią zmienia swój kierunek i nie wnosi pełnego wkładu w uporządkowany ruch ładunków w kierunku pola elektrycznego. Jest to zależność liniowa od temperatury.

Pasma energetyczne kryształów.

Pasmowa teoria przewodnictwa elektrycznego - kwantowo mechaniczna teoria opisująca przewodnictwo elektryczne. W przeciwieństwie do teorii klasycznej punktem wyjścia w tej teorii jest statystyka Fermiego-Diraca i falowa natura elektronów. Najważniejszym pojęciem tej teorii jest pasmo energetyczne - jest to przedział energii, jaką mogą posiadać elektrony w przewodniku. Istnienie ciągłego widma energetycznego jest związane z oddziaływaniem na siebie poszczególnych atomów (jest to zbiór bardzo blisko położonych widm liniowych), natomiast występowanie obszarów zabronionych wynika z warunków nakładanych na periodyczność funkcji falowej elektronów.

Teoria pasmowa jest związana z budową atomu. Energia elektronów nie może bardzo różnić się od siebie, lecz nie może zdarzyć się sytuacja, gdzie więcej niż dwa elektrony będą miały taka samą energię

Zależność przewodnictwa elektrycznego półprzewodników samoistnych od temperatury.

Przewodnictwo półprzewodników rośnie ze wzrostem temperatury.

Według pasmowej teorii ciała stałego w temp. 0 K pasmo walencyjne półprzewodników jest

całkowicie wypełnione elektronami i pole elektr. nie może zmienić ani położenia, ani pędu

poszczególnych elektronów, a więc wywołać przepływu prądu elektr.; aby elektron mógł

uczestniczyć w przepływie prądu, musi zostać przeniesiony do pasma przewodnictwa

(następnego pasma pustego lub niecałkowicie zapełnionego), oddzielonego od pasma

walencyjnego tzw. pasmem wzbronionym (przerwą energetyczną).Już w temperaturze

pokojowej pewna liczba elektronów zostaje przeniesiona do pasma przewodnictwa, liczba ta

rośnie ze wzrostem temperatury.

W półprzewodnikach samoistnych przewodnictwo zależy tylko od liczby elektronów przeniesionych z pasma walencyjnego do pasma przewodnictwa i dziur pozostawionych przez nie w paśmie walencyjnym.

OPIS DOŚWIADCZENIA

Zmontowałam układ ściśle według instrukcji. Połączyłam 3 omomierze z grzejnikiem podłączonym do sieci. Włączyłam zasilanie i mierzyłam wskazania wszystkich trzech omomierzy co 5 stopni Celsjusza. Wyniki notowałam w tabeli, najpierw ogrzewając układ od temperatury pokojowej do stu stopni, a następnie wyłączyłam zasilacz i notowałam wskazania przyrządów podczas chłodzenia układu.

OPRACOWANIE WYNIKÓW POMIARÓW

Na podstawie wyników pomiarów omomierzy można stwierdzić jednoznacznie, iż urządzenie drugie wskazywało własności metalu, pierwsze- termistora, a trzecie- manganinu. Jak bowiem wynika z podstawowych praw elektryczności, opór metali rośnie ze wzrostem temperatury (na skutek zmian w poruszaniu się elektronów walencyjnych poszczególnych atomów), a dla termistora maleje. Manganin jest to stop miedzi (ok. 85%) z manganem (ok. 12%) i niklem (ok. 3%), charakteryzujący się bardzo małym stałym współczynnikiem cieplnym oporu elektrycznego. Stosowany jest do produkcji oporników wzorcowych oraz oporników precyzyjnych przyrządów elektrycznych.

Obliczam wartości logarytmów wartości średnich oporu dla termistora dla kolejnych temperatur oraz przeliczam wartości temperatur w stopniach Celsjusza na Kelwiny, by sporządzić wykres:

Omomierz 1		Wartość średnia	Logarytm naturalny z wartości średniej
ogrzewanie	chłodzenie
0,157±0,001	0,156±0,001	0,1565±0,001	-1,855
0,128±0,001	0,131±0,001	0,1295±0,001	-2,044
0,104±0,001	0,110±0,001	0,107±0,001	-2,235
0,088±0,001	0,093±0,001	0,0905±0,001	-2,402
0,075±0,001	0,079±0,001	0,077±0,001	-2,564
0,063±0,001	0,067±0,001	0,065±0,001	-2,733
0,054±0,001	0,057±0,001	0,0555±0,001	-2,891
0,046±0,001	0,049±0,001	0,0475±0,001	-3,047
0,038±0,001	0,042±0,001	0,040±0,001	-3,219
0,034±0,001	0,036±0,001	0,035±0,001	-3,352
0,029±0,001	0,031±0,001	0,030±0,001	-3,506
0,025±0,001	0,027±0,001	0,026±0,001	-3,649
0,022±0,001	0,023±0,001	0,0225±0,001	-3,794
0,019±0,001	0,020±0,001	0,0195±0,001	-3,937
0,017±0,001	0,018±0,001	0,0175±0,001	-4,045
0,015±0,001		0,015±0,001	-4,199

[°C]	[K]
25±0,1	298±0,1
30±0,1	303±0,1
35±0,1	308±0,1
40±0,1	313±0,1
45±0,1	318±0,1
50±0,1	323±0,1
55±0,1	328±0,1
60±0,1	333±0,1
65±0,1	338±0,1
70±0,1	343±0,1
75±0,1	348±0,1
80±0,1	353±0,1
85±0,1	358±0,1
90±0,1	363±0,1
95±0,1	368±0,1
100±0,1	373±0,1

Wartość temperaturowego współczynnika oporu dla drutu miedzianego:

Obliczam niepewność pomiaru w oparciu o metodę najmniejszych kwadratów, ponieważ niepewności przypisane punktom pomiarowym są jednakowe

Niepewności standardowe u(a) i u(b)

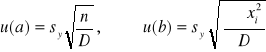
, przy czym
i

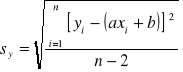
x_i kolejne wartości 1/T

y_i kolejne wartości lnR

n ilość pomiarów (16)

Σx_iy_i = -0,1458

Σx_i = 0,0479

Σy_i = -49,472

(Σx_i)² = 2,29*10^-3

(Σy_i)² = 2447,48

Σx_i² = 1,44*10^-4

a = 2636,34

b= -10,01

obliczam niepewności standardowe:

S_y=√[15,748:14]=1,06

D=1,4*10^-5

u(a)=10,6*1069,04=1133,18

u(b)=3,207*1,06=3,399=3,4

stąd

a= 2636,34±1133,18 = [1503,16 ; 3769,52]

b= -10,01±3,4 = [-6,61 ; -13,41]

**************************

Aby obliczyć E_g należy skorzystać ze wzoru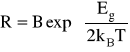
, po zlogarytmowaniu przekształconego na: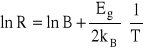
. Po narysowaniu wykresu lnR=f(1/T) otrzymujemy prostą o współczynniku kierunkowym równym E_g/2k_B. Obliczony z najmniejszych kwadratów współczynnik ten wynosi 2636,34. Znając wartość stałej Boltzmanna k_B = 8.62 × 10^-5 eV, możemy obliczyć E_g.

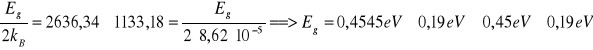
WNIOSKI

Dla materiału badanego przez omomierz drugi obliczona wartość szerokości przerwy energetycznej wynosi [0,26;0,64] eV. Ponieważ otrzymany wynik jest mniejszy od 2 eV, badany materiał jest półprzewodnikiem.

Z uzyskanych w doświadczeniu pomiarów można wywnioskować, że badane omomierzami materiały to po kolei-termistor, miedź i manganin. W pomiarach termistora opór maleje ze wzrostem temperatury, a obliczenia wskazują, iż ma on właściwości półprzewodnika. Opór metalu rośnie wraz z podnoszeniem się temperatury, co jest spełnione w pomiarach omomierza 2. Natomiast omomierz 3 praktycznie nie zauważył zmian oporu ze zmianą temperatury- takie właściwości ma między innymi manganin, mający bardzo mały współczynnik cieplny oporu elektrycznego.

---