Wydział Inżynierii Lądowej	Rafał Tyrka	Zespół: 3	Data: 28.03.2014
Grupa 16	WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA PROSTEGO	Nr. Ćw.: 1	Ocena:

1.Wprowadzenie

Przyspieszenie ziemskie g jest to przyspieszenie ciał spadających swobodnie w polu grawitacyjnym Ziemi (przy braku oporów ruchu). Z prawa powszechnej grawitacji Newtona można wyliczyć, że na powierzchni Ziemi jego wartość dana jest wzorem:

Gdzie:

G- stała grawitacji
6,67*10^-11 [N*m²/kg²]

M_z- masa Ziemi
5,98*10²⁴[kg];
R_z- promień Ziemi
6370[km].

Zatem na biegunach gdzie promień naszej planety jest najmniejszy, będzie ono miało największą wartość. Na wartość przyspieszenia wpływa również ruch obrotowy Ziemi - związane z nim przyspieszenie odśrodkowe zmniejsza mierzone przyspieszenie ziemskie na wszystkich szerokościach geograficznych poza biegunami. Oczywiście wartość przyspieszenia ziemskiego maleje wraz z wysokością nad powierzchnią Ziemi.

2.Metoda Pomiaru

Przyspieszenie ziemskie można obliczyć za pomocą wahadła prostego(wahadło proste to mała, metalowa kulka zawieszona na nierozciągliwej, lekkiej nici; ciężar kulki jest często pomijany). Po wychyleniu kulki z punktu równowagi i swobodnym jej puszczeniu wykonuje ona ruch drgający prosty.

Za ruch kulki odpowiedzialna jest składowa jej ciężaru, która jest styczna do toru:



Przy niewielkim wychyleniu czyli α<5° przyjmujemy że sinα wynosi α, a ruch kulki jest harmoniczny prosty
. Kątowe wychylenie kulki α jest funkcją okresową czasu w okresie:

Gdzie: l- długość wahadła;
g- wartość przyspieszenia ziemskiego

W przypadku gdy znamy zarówno długość wahadła jak i okres jego drgań możemy wyznaczyć wartość przyspieszenia ziemskiego korzystając z przekształconego wzoru:

3.Pomiary i obliczenia

W celu wyznaczenia długość wahadła dokonujemy pomiaru długości nici metrem o niepewności systematycznej 0,1 [cm]. Następnie dokonujemy pomiaru kulki suwmiarką elektroniczną o niepewności systematycznej 0,01 [mm]. Wyżej wymienione pomiary przedstawiają się następująco:

s= 73[cm] +/- 0,1[cm]- to długość nici;
2r=2,01[cm] +/- 0,01[mm] - średnica kulki.

Niepewności systematyczne:

=0,01[mm]- niepewność systematyczna średnicy;

=0,01[mm]*0,5=0,005[mm]- niepewność systematyczna promienia.

Okres drgań wahadła nie zależy od masy kulki, ani tez amplitudy drgań. Za pomocą stopera o niepewności systematycznej 0,2[s] w ciągu 10T=>0,02 na 1T i mierzymy czas 10 okresów.

L.p.	10Ti	Ti	   	^
1.	17,04	1,704	0,027	0,000702
2.	17,34	1,734	-0,004	0,000012
3.	17,53	1,753	-0,023	0,000506
4.	17,42	1,742	-0,012	0,000132
5.	17,09	1,709	0,021	0,000462
6.	17,53	1,753	-0,023	0,000506
7.	17,07	1,707	0,023	0,000552
8.	17,29	1,729	0,001	0,000002
9.	17,25	1,725	0,005	0,000030
10.	17,49	1,749	-0,019	0,000342
		=1,7305

= 0,003246[s]

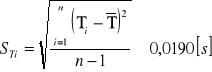
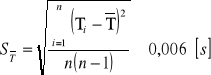
Δ_dT = 0,1 [s]

r = 0,0105 [m]

s=0,73 [m]

4.Błędy pomiarowe:

• Niepewność kwadratowa przyspieszenia ziemskiego:

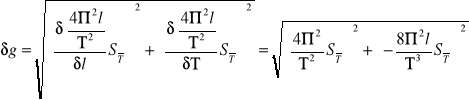
• Niepewność maksymalna

• Niepewność procentowa

Ostateczny wynik przyciągania ziemskiego:

5.WNIOSKI:

Wyznaczone doświadczalnie przyspieszenie ziemskie wyniosło
Tablicowe przyspieszenie dla Krakowa wynosi
. Wartość wyznaczona zawiera się w dopuszczalnej granicy błędu.

Na niedokładność pomiaru miała wpływ niedoskonałość ludzkich zmysłów oraz mało precyzyjne narzędzia miernicze używane przez prowadzących doświadczenie. Dodtkowym czynnikiem zakrzywiającym wynik pomiaru był brak uwzględnienia pod uwagę oporu powietrza itp.

---