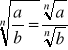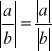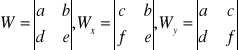ALGEBRA 1

POTĘGA

OZNACZENIA:

DEFINICJE:

a^n=

a^0 = 1

a^-1 =

WŁASNOŚCI:

a^m a^n = a^m+n

= a^m-n

(ab)= a^nb^n

=

(a^m)^n = a^mn

PIERWIASTEK

DEFINICJE:

1) n P',

2) n P',

WŁASNOŚCI:

UWAGA:

LOGARYTM

DEFINICJA: a>0
> 0
b

WŁASNOŚĆI:	logpab = logpa + logpb
a^b=e^blna	logp

WARTOŚĆ BEZWZGLĘDNA

DEFINICJA:
x dla x

-x dla x< 0

WŁASNOŚCI:

FUNKCJA LINIOWA 2

RÓWNANIE LINIOWE

y = ax + b, a y b 0 x 1 1)

y = 0 y x 2)

y = b, b 3)

DEFINICJA: ax + b = 0

KLASYFIKACJA:

1. równanie niezależna (oznaczone) [jedno rozwiązanie]

2. równanie zależne (nieoznaczone, tożsamościowe) [rozwiązaniem jest zbiór R]

3. równanie sprzeczne [brak rozwiązań] [rozwiązaniem jest zbiór
   ]

NIERÓWNOŚĆ LINIOWA

KLASYFIKACJA:

1. nierówność warunkowa [rozwiązaniem jest podzbiór R różny od R]

2. nierówność bezwarunkowa (tożsamościowa) [rozwiązaniem jest zbiór R]

3. nierówność sprzeczna [brak rozwiązań] [rozwiązaniem jest zbiór
   ]

UKŁAD LINIOWY

DEFINICJA:

ax + by = c dx + ey = f

KLASYFIKACJA:

1. układ niezależny (oznaczony) [jedno rozwiązanie]

2. układ zależny (nieoznaczony) [nieskończony zbiór rozwiązań]

3. układ sprzeczny [brak rozwiązań] [rozwiązaniem jest zbiór
   ]

TWIERDZENIE CRAMERA: Jeżeli


i

DYSKUSJA:

1) układ niezależny: W

2) układ zależny: W = 0

3) układ sprzeczny:

hghghg

---