FUNKCJA POTĘGOWA, WYKŁADNICZA I LOGARYTMICZNA
Należy powtórzyć:
potęga o wykładniku naturalnym, całkowitym ujemnym, wymiernym;
własności działań na potęgach;
określenie i własności pierwiastka arytmetycznego, działania na potęgach;
określenie funkcji równych, przykłady wykresów funkcji potęgowych;
określenie i własności funkcji wykładniczej;
określenie i własności logarytmu;
określenie i własności funkcji logarytmicznej;
równania i nierówności pierwiastkowe;
równania i nierówności potęgowe;
równania i nierówności logarytmiczne;
układy równań i nierówności wykładniczych i logarytmicznych;
równania i nierówności logarytmiczne i wykładnicze z parametrem.
Oblicz :
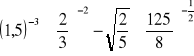
Usuń niewymierność z mianowników ułamków:
Wykaż, że
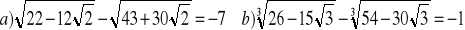
Wyznacz dziedziny i naszkicuj wykresy funkcji
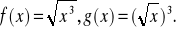
Czy funkcje te są równe?Naszkicuj wykresy i opisz własności funkcji:
Wyznacz dziedzinę funkcji:
Rozwiąż równania:
Rozwiąż nierówności:
Naszkicuj wykres funkcji:
Zbadaj monotoniczność funkcji y=3x w oparciu o definicję.
Zbadaj z definicji różnowartościowość funkcji y=(1/3)x.
Rozwiąż równania i nierówności:
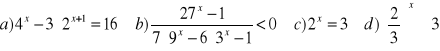
Wyznacz dziedzinę funkcji i zapisz ją w postaci sumy przedziałów:
Naszkicuj wykres funkcji:
Z definicji udowodnij, że funkcja
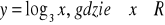
jest różnowartościowa.Z definicji udowodnij, że funkcja
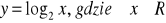
jest rosnąca.Z definicji udowodnij, że funkcja
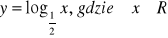
jest malejąca.Rozwiąż równania i nierówności:
Rozwiąż równania i nierówności:
Dane są zbiory:
Zaznacz w prostokątnym układzie współrzędnych zbiór

, jeżeliNaszkicuj wykres funkcji f(m) liczby rozwiązań równania
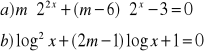
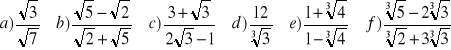
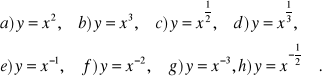
![]()
.
![]()
.
![]()
.
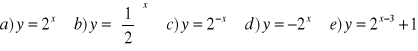
![]()
.
![]()
.
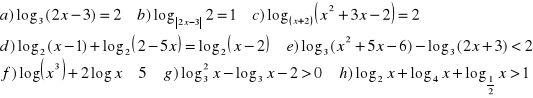
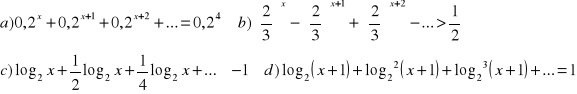
![]()
![]()
.
Zapisz za pomocą przedziałów zbiory: ![]()
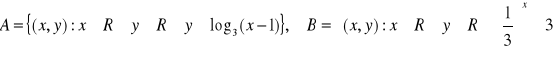
w zależności od wartości parametru m.
1
Wyszukiwarka
Podobne podstrony:
9011
9011
9011
9011
więcej podobnych podstron