WB |
„Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej” |
24.05.2009 |
Nr 10 |
|
|
Długość fali — najmniejsza odległość pomiędzy dwoma punktami o tej samej fazie drgań (czyli pomiędzy dwoma powtarzającymi się fragmentami fali — zob. rysunek). Dwa punkty fali są w tej samej fazie, jeżeli wychylenie w obu punktach jest takie samo i oba znajdują się na etapie wzrostu (lub zmniejszania się). Jeżeli w jednym punkcie wychylenie zmniejsza się a w drugim maleje, to punkty te znajdują się w fazach przeciwnych.
Tradycyjne długość fali oznacza się ją grecką literą λ. Dla fali sinusoidalnej najłatwiej określić jej długość wyznaczając odległość między dwoma sąsiednimi grzbietami.
Interferencja (łac. inter - między + ferre - nieść) to zjawisko nakładania się fal prowadzące do zwiększania lub zmniejszania amplitudy fali wypadkowej. Interferencja zachodzi dla wszystkich rodzajów fal, we wszystkich ośrodkach, w których mogą rozchodzić się dane fale. W ośrodkach nieliniowych oprócz interferencji zachodzą też inne zjawiska wywołane nakładaniem się fal, w ośrodkach liniowych fale ulegając interferencji spełniają zasadę superpozycji.
Obliczenia:
Wartość stałej siatki dla prążków dla lampy sodowej:
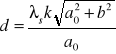
, λs= 588,9nm = 0,0000005889m
Prążek 1:
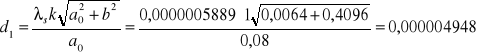
Prążek 2:
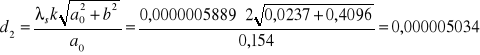
Prążek 3:
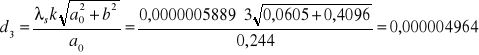
![]()
0,000004982 [m] = 4982 [nm]
Maksimum przepuszczalności filtrów dla lampy mikroskopowej:
![]()
dla światła niebieskiego
![]()
nm
![]()
nm
![]()
nm
![]()
nm
dla światła zielonego
![]()
nm
![]()
nm
![]()
nm
![]()
nm
dla światła pomarańczowego
![]()
nm
![]()
nm
![]()
nm
![]()
nm
dla światła czerwonego
![]()
nm
![]()
nm
![]()
nm
![]()
nm
∆d(a0) = 0,001m
∆e(a0) = 0,003m 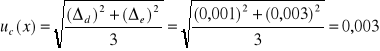
m
∆d(b) = 0,01m
∆e(b) = 0,02m 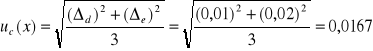
m
Niepewność pomiarowa:
dla lampy sodowej:
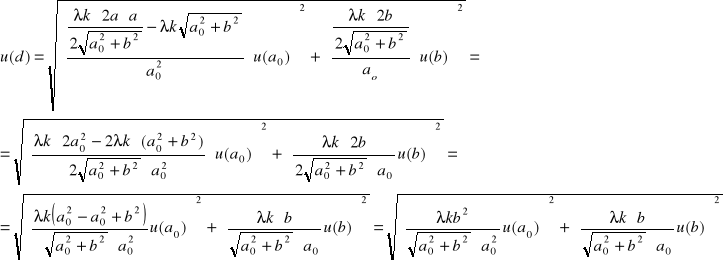
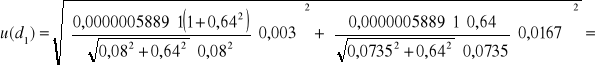
= 0,000000068 m = 68 nm
u(d1) = 0,000000074 m = 74 nm
u(d1) = 0,000000055 m = 55 nm
Uc(dśr) = ![]()
= 83 nm
dla lampy mikroskopowej:

światło zielone: λśr = 19 nm
λz1 = 0,000000011 m = 11 nm
λz2 = 0,000000018 m = 18 nm
λz3 = 0,000000028 m = 28 nm
światło pomarańczowe: λśr = 19,6 nm
λp1 = 0,000000009 m = 9 nm
λp2 = 0,000000020 m = 20 nm
λp3 = 0,000000030 m = 30 nm
światło czerwone: λśr = 21,7 nm
λc1 = 0,000000010 m = 10 nm
λc2 = 0,000000022 m = 22 nm
λc3 = 0,000000033 m = 33 nm
światło niebieskie: λśr = 14,7 nm
λn1 = 0,000000007 m = 7 nm
λn2 = 0,000000014 m = 14 nm
λn3 = 0,000000023 m = 23 nm
Wnioski
W ćwiczeniu miałem obliczyć długość fali na poszczególnych filtrach. Po przeprowadzeniu obliczeń okazało się ze każda długość fali mieści się w granicy błędu podanymi na filtrach. Dla światła fioletowego wartości podane na filtrze wynosiły 442+/-6nm oraz 359+/-7nm, obliczona wartość wynosi 451nm, zatem prawidłowa była pierwsza z podanych długości.
Wyszukiwarka
Podobne podstrony:
Ćw 85-Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej
Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej, Wrocław, dn. 16.11.94
Ćw 85 Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej
Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej 3 DOC
Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej
Pomiar długości fali świetlnej za pomocą siatki dyfrakcyjnej i spektrometru, fizyka labo
Wyznaczanie długości fali światła za pomocą siatki dyfrakcyjnej, Monika Wojakowska
fizyka sprawozdania, Pomiar długości fali świetlnej za pomocą siatki dyfrakcyjne, Sprawozdanie z ćwi
przew met termistor, Pomiar długości fali świetlnej za pomocą siatki dyfrakcyjnej
więcej podobnych podstron