Dominik Trojnar 2005-10-24

I TD, gr. Lab. 02

Sprawozdanie z ćwiczenia nr 40

Zjawisko fotoelektryczne wewnętrzne. Wyznaczanie charakterystyki fotooporu.

Zagadnienia do samodzielnego opracowania

Zjawisko fotoelektryczne zewnętrzne i wewnętrzne jako wynik oddziaływania promieniowania z materią.

Zjawisko fotoelektryczne zewnętrzne polega na wyrzuceniu elektronów z powierzchni ciała stałego pod wpływem padającego nań światła (promieniowania). Zjawisko to zachodzi najskuteczniej, gdy promieniowanie ma niewielką długość fali, a ciało jest metalem. Zjawisko to określa się też mianem fotoemisji elektronowej. Dla danego przewodnika, z którego elektrony są wybijane istnieje długość graniczna, dla której zachodzi zjawisko. Dla fal dłuższych od granicznej zjawisko to nie zachodzi. Zjawisko to można wytłumaczyć tylko za pomocą teorii kwantowej światła traktując światło jako zbiór pewnych porcji energii zwanych fotonami lub kwantami promieniowania.

Oprócz zjawiska fotoelektrycznego zewnętrznego istnieje też zjawisko fotoelektryczne wewnętrzne występujące w półprzewodnikach. Polega na tworzeniu dodatkowych elektronów swobodnych w wyniku absorpcji światła padającego na półprzewodnik oraz na wzroście przewodnictwa kryształu w skutek zwiększenia liczby elektronów swobodnych i dziur pod wpływem światła. Wykorzystane jest to w bateriach słonecznych.

Prawa zjawiska fotoelektrycznego.

Jeśli wytworzymy pewną różnicę potencjałów pomiędzy płytką A, z której uwalniane są elektrony, a płytką zbierającą B, to zaobserwujemy przepływ prądu. Gdy U jest dostatecznie duże, wtedy prąd fotoelektryczny osiąga pewną wartość graniczną (prąd nasycenia). Niektóre z elektronów dochodzą do elektrody B, pomimo że pole elektryczne działa na ich ruch hamująco. Jednakże gdy różnica potencjałów U jest dostatecznie duża, równa wielkości U₀ zwanej napięciem hamującym, wtedy prąd fotoelektryczny całkowicie zanika. Różnica potencjałów U₀ pomnożona przez ładunek elektronu jest miarą energii kinetycznej K_max najszybszych uwolnionych elektronów:

Gdy na metalową płytkę pada fala elektromagnetyczna i powoduje ona wybijanie elektronów, to teoretycznie, jeżeli wzięlibyśmy większe natężenie światła (mamy większe natężenie pola elektromagnetycznego), powinniśmy (zależnie od siły, a niezależnie od częstotliwości) zawsze obserwować efekt fotoelektryczny. A jednak okazuje się, że poniżej pewnej częstotliwości (granicznej) nie potrafimy tego wykryć.

Zjawisko fotoelektryczne ma trzy podstawowe cechy, których nie można wyjaśnić na gruncie klasycznej falowej teorii światła:

1. Z falowej teorii światła wynika, że amplituda oscylującego pola elektrycznego E fali świetlnej wzrasta, gdy wzrasta natężenie wiązki światła. Ponieważ siła działająca na elektron jest równa eE, z zależności tej wynika, że energia kinetyczna fotoelektronów również powinna wzrosnąć, gdy zwiększamy natężenie wiązki światła. Jednakże K_max jest niezależne od natężenia światła.

2. Zjawisko fotoelektryczne powinno występować dla każdej częstotliwości światła, pod warunkiem, że natężenie światła jest wystarczająco duże, aby dostarczona została energia konieczna do uwolnienia elektronów. Jednak dla każdej powierzchni istnieje pewna charakterystyczna częstotliwość graniczna
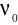
   . Dla częstotliwości światła mniejszej od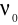
   zjawisko fotoelektrycznej nie występuje, niezależnie od tego, jak silne jest oświetlenie powierzchni.

3. Według teorii klasycznej energia świetlna jest jednorodnie rozłożona na całej powierzchni falowej. Zatem gdy wiązka światła jest dostatecznie słaba, powinno występować mierzalne opóźnienie czasowe pomiędzy chwilą, kiedy światło zaczyna padać na powierzchnię płytki, a momentem uwolnienia z niej elektronu. W tym właśnie czasie elektron powinien absorbować energię z wiązki światła aż do momentu, gdy nagromadzona energia będzie wystarczająca, aby elektron mógł wydobyć się z metalu. Jednak nigdy nie stwierdzono żadnego mierzalnego opóźnienia czasowego.

Einstein zakwestionował słuszność klasycznej teorii światła i zaproponował nową teorię. Założył, że energia jest skwantowana, a mianowicie skoncentrowana w oddzielnych porcjach (kwantach światła), które później nazwane zostały fotonami. Wyniki doświadczeń interferencyjnych i dyfrakcyjnych zdecydowanie wskazują na to, że fotony nie rozchodzą się jak klasyczne cząstki, ale jak klasyczne fale w tym sensie, że obliczenia oparte na propagacji tych fal w sposób poprawny wyjaśniają pomiary dotyczące średniego rozchodzenia się dużej liczby fotonów. Einstein skupił uwagę na procesach emisji i absorpcji promieniowania i był pierwszym, który zdał sobie sprawę z tego, że w procesach tych dochodzą do głosu korpuskularne własności promieniowania. Einstein założył, że porcja emitowanej energii jest początkowo zlokalizowana w przestrzeni i że pozostaje ona nadal zlokalizowana, gdy oddala się z prędkością światła od źródła. Założył on dalej, że ilość energii E zawarta w fotonie związana jest z jego częstotliwością następującą zależnością

Einstein założył również, że w zjawisku fotoelektrycznym jeden foton jest całkowicie absorbowany przez jeden elektron. Gdy elektron emitowany jest z powierzchni metalu, wtedy jego energia kinetyczna wynosi

gdzie hv₀ jest energią zaabsorbowanego fotonu, a W jest pracą potrzebną do uwolnienia elektronu z metalu. Praca ta potrzebna jest do pokonania sił przyciągania pochodzących od atomów z powierzchni płytki oraz na pokrycie strat energii kinetycznej wskutek zderzeń elektronu wewnątrz płytki. W przypadku najsłabiej związanego elektronu i braku strat wewnątrz płytki, wychodzący elektron będzie miał maksymalną energię kinetyczną K_max:

gdzie W₀, energia charakterystyczna dla danego metalu, zwana pracą wyjścia, jest minimalną energią potrzebną elektronowi na pokonanie sił przyciągania wiążących go wewnątrz metalu, przekroczenie powierzchni i wydobycie się na zewnątrz. Rozważmy, w jaki sposób nowa teoria wyjaśnia trzy cechy zjawiska fotoelektrycznego:

1. Brak zależności K_max od natężenia światła. Zwiększanie natężenia światła zwiększa jedynie liczbę fotonów, a więc także prąd elektryczny. Nie zmienia zaś energii hv pojedynczych fotonów.

2. Istnienie częstotliwości progowej. Jeśli K_max=0, to
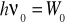
   , co zapewnia, że padający foton o częstotliwości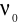
   ma energię wystarczającą na wybicie elektronu z metalu. Jeśli częstotliwość zostanie zmniejszona poniżej
   , to pojedyncze fotony (niezależnie od ich liczby, a więc od natężenia światła) nie będą miały energii wystarczającej do uwolnienia elektronu.

3. Brak opóźnienia czasowego emisji elektronów. Zgodnie z tą teorią energia skoncentrowana jest w porcjach, a nie rozłożona na całej powierzchni. Jeśli na płytkę pada światło nawet o małym natężeniu, to przynajmniej jeden foton zostanie zaabsorbowany przez elektron i uwolni go.

Budowa i zasada działania fotooporu i fotoogniwa.

Budowa fotoopornika

W momencie oświetlenia opór fotoopornika maleje, gdyż wzrasta liczba nośników odpowiedzialnych za przepływ prądu elektrycznego. Ponieważ zjawisko fotoelektryczne wewnętrzne zachodzi jedynie w cienkiej warstwie powierzchniowej, stąd fotoopór zbudowany jest z cienkiej i długiej taśmy półprzewodnika. Przed uszkodzeniami mechanicznymi taśma jest chroniona warstwą szkła organicznego.

Inne efekty wywołuje zjawisko fotoelektryczne na złączach metal-półprzewodnik. Wiązka światła padająca na styk zakłóca stan równowagi dynamicznej warstwy podwójnej. Kwanty światła przekazują swoją energię elektronom. W półprzewodniku przenoszą elektrony z pasma walencyjnego do pasma przewodnictwa. Zatem w półprzewodniku wzrasta ilość swobodnych elektronów, które w warunkach istniejącej równowagi dynamicznej przechodzą natychmiast do metalu, ładując go ujemnie. Oświetlone złącze staje się źródłem prądu i jest nazwane fotoogniwem. Na rysunku poniżej pokazano budowę fotoogniwa miedziowego.

Na miedzianym podłożu znajduje się warstwa tlenku miedzi CuO, który jest półprzewodnikiem typu p. Na powierzchni tlenku znajduje się cienka przeźroczysta warstwa metalu: srebra lub miedzi. Na górnym złączu CuO-metal światło przenosi pewną ilość elektronów do pasma przewodnictwa, które natychmiast przechodzą do metalu, ładując go ujemnie. Na drugim złączu zjawisko to nie występuje, ponieważ światło nie przenika przez warstwę CuO.

Wykonanie ćwiczenia:

1. Obwód został połączony według schematu podanego w instrukcji do ćwiczenia.

2. Przy stałej wartości napięcia zasilającego została znaleziona odległość źródła światła do fotoopornika taka, że natężenie prądu wynosiło 3mA.

3. Odczytywanie wartości natężenia dla odległości wynoszącej 20, 25, 30, 40, 60 i 80 cm.

Wyniki pomiarów:

Klasa przyrządów:

• Woltomierz: 0,5

• Miliamperomierz: 0,5

Błędy spowodowane działaniem przyrządów:

• Woltomierz:
  

• Miliamperomierz:
  

Zakres przyrządów:

• Woltomierz: 0-30V

• Miliamperomierz: 0-3mA

Błędy odczytu
,
i
zostały podane w tabeli.

Błąd
obliczony został ze wzoru:

U [V]	ΔU [V]	r [m]	Δr [m]			I [mA]	ΔI [mA]
20,5	0,015	0,161	0,005	38,58	2,40	3	0,015
					0,2			25,00	1,25	1,8
					0,25			16,00	0,64	0,9
					0,3			11,11	0,37	0,55
					0,4			6,25	0,16	0,25
					0,6			2,78	0,05	0,1
					0,8			1,56	0,02	0,05

Wnioski:

Zjawisko fotooporu może zostać użyte do sterowania przepływem prądu, szczególnie do automatycznego włączania np. oświetlenia po zmierzchu

---