I EiT	ZABOR JAKUB	16.03.2006
Ćwiczenie nr 6	Pomiar długości fali świetlnej na podstawie interferencji w układzie optycznym do otrzymywania pierścieni Newtona	Ocena:

1. Uwagi:

2. Wstęp:

Dla fal elektromagnetycznych, tak samo jak dla fal sprężystych spełniona jest zasada superpozycji fal. Zasada ta mówi, że fale rozchodzą się w przestrzeni niezależnie od siebie. Superpozycja dwu lub więcej fal harmonicznych o tych samych częstościach pozwala na sumowanie ich w każdym punkcie przestrzeni, w wyniku czego obserwuje się interferencję. Obraz interferencji dwóch fal można obserwować tylko wtedy, gdy różnice faz między tymi falami są stałe w czasie obserwacji. Fale takie nazywamy spójnymi. Spójne wiązki światła można otrzymać rozdzielając (przez odbicie lub załamanie) an dwie wiązki światło wysyłane przez niewielki obszar źródła rozciągłego. Każdy ciąg falowy ulega przy tym rozdzieleniu na dwa ciągi falowe wchodzące w skład dwu różnych wiązek. Ciągi te są ze sobą spójne i mogą dać stały obraz interferencyjny, niezależnie od tego, przez który atom i w jakiej chwili zostały wysłane. Obraz powstający na ekranie w wyniku interferencji spójnych wiązek światła monochromatycznego jest taki, jak gdyby interferowały proste fale harmoniczne.

Rozdzielenie wiązki światła na dwie wiązki zawierające po jednej części każdego ciągu falowego uzyskuje się m.in. w układzie do otrzymania pierścieni Newtona. Obraz interferencyjny w postaci prążków w kształcie współśrodkowych okręgów uzyskuje się tu przez umieszczenie soczewki płasko - wypukłej o dużym promieniu krzywizny na płaskiej płytce szklanej, pomiędzy którymi istnieje cienka warstwa powietrza o stopniowo rosnącej grubości w miarę oddalania się od punktu centralnego (styczności). Monochromatyczne promienie równoległe, padające prostopadle na płaską powierzchnię soczewki przechodzą przez szkło i częściowo ulegają odbiciu od powietrza (na drugiej powierzchni granicznej soczewki), a częściowo przechodzą dalej przez warstwę powietrza, ulegają odbiciu od płytki szklanej i wracają do obserwatora. Część wiązki odbita i ta, która dwukrotnie przeszła przez warstwę powietrza o grubości d odbijając się interferują ze sobą. Różnica ich dróg optycznych wynosi:

Wielkość wynika ze zmiany fazy na przeciwną przy odbiciu od ośrodka optycznie gęstszego na powierzchni płytki.

Rys.Geometryczna interpretacja warunku interferencji.

W celu ustalenia zależności między promieniami pierścieni jasnych lub ciemnych i długością fali przeprowadzamy analizę geometryczną:

Ponieważ d jest bardzo małe w porównaniu z 2R, można ostatnią zależność wyrazić:

Gdy różnica dróg optycznych równa się nieparzystej wielokrotności połówek długości fali, powstaje pierścień ciemny o promieniu r_n:

Podstawiając kolejno za n 1,2,3 . . .,a następnie odejmując stronami dowolną parę równań otrzymujemy:

3. Tabela pomiarowa:

Rodzaj światła	Rząd pierścieni ciemnych	Odczyt z mikrometru		Średnia wartość promienia pierścienia r [mm]	Promień krzywizny soczewki R[mm]	Długość fali λ [nm]
							w przód [mm]	w tył [mm]
	Sodowe	4	1,15	1,20			1,18	472,26	------
		8	1,55	1,60			1,58
		12	1,86	1,94			1,9
		16	2,17	2,20			2,19
		20	2,38	2,43			2,41
		24	2,60	2,64			2,62
		28	2,81	2,85			2,83
		32	2,99	3,06			3,03
	Filtr 1	4	1	0,94		0,97	472,26	-----
		8	1,49	1,34		1,42		569,34
		12	1,75	1,63		1,69		444,51
		16	2	1,87		1,94		480,40
		20	2,27	2,03		2,15		454,68
		24	2,40	2,18		2,29		329,06
		28	2,52	2,32		2,42		324,13
		32	2,66	2,46		2,56		369,08
	Filtr 2	4	1,23	1,04		1,14	472,26	-----
		8	1,33	1,39		1,36		291,15
		12	1,59	1,75		1,67		497,24
		16	1,72	2,03		1,88		394,64
		20	1,91	2,38		2,15		576,01
		24	2,19	2,76		2,48		808,82
		28	2,29	3,24		2,77		805,96
		32	2,38	3,50		2,94		513,86

4. Obliczenia:

1. Wyznaczenie promienia krzywizny soczewki.

Promień krzywizny należy mierzyć w dwie strony od środka w celu uśrednienia wartości. Promień ten wyznaczamy przy oświetleniu monochromatyczną wiązką światła o znanej długości fali, otrzymaną z palnika sodowego przystawionego do oświetlacza. Po ustawieniu ostrości mikroskopu, naprowadzić punkt centralny pierścieni tak, aby pokrywał się z przecięciem krzyża na okularze mikroskopu. Następnie ustawiamy czujnik mikrometryczny na połowę zakresu wskazań, co umożliwia pomiar promieni pierścieni w obydwie strony względem punktu centralnego. Promienie pierścienia wyliczmy przekształcając wzór na λ:

gdzie:

• λ_Na - długość fali równa 589^. 10 ^-9 m

• r_m, r_n przyjmowane odpowiednio wartości

• n = 4

• Δr = 0,04 mm

zatem


[mm]


[mm]


[mm]


[mm]


[mm]


[mm]


[mm]

Każdy z wyników został dodatkowo w trakcie obliczeń podzielony przez 10³ w celu uzyskania końcowego wyniku w [mm].

Średnia wartość promienia krzywizny soczewki wynosi:

R_śr = (R₂+R₃+R₄+R₅+R₆+R₇+R₈)/7 = 472,26 [mm]

1. Wyznaczanie długości fali światła monochromatycznego otrzymanego przy użyciu filtrów interferencyjnych.

W tej części ćwiczenia należy użyć lampki mikroskopowej z żarowym źródłem światła, a następnie między nią a oświetlaczem umieścić filtr interferencyjny. Pomiar promieni przeprowadzamy w sposób podobny jak w pierwszej części ćwiczenia. Następnie obliczamy długość fali ze wzoru

gdzie:

• R = 472,26 [mm]

• Δr = 0,04 [mm]

• r_m, r_n przyjmowane odpowiednio wartości

zatem

♦Filtr 1


[nm]


[nm]


[nm]


[nm]


[nm]


[nm]


[nm]

Każdy z wyników został dodatkowo w trakcie obliczeń podzielony przez 10^-6 w celu uzyskania końcowego wyniku w [nm].

Średnia wartość długości fali wynosi

λ_śr = (λ₂+λ₃+λ₄+λ₅+λ₆+λ₇+λ₈)/7 = 424,46 [nm]

♦Filtr 2


[nm]


[nm]


[nm]


[nm]


[nm]


[nm]


[nm]

Każdy z wyników został dodatkowo w trakcie obliczeń podzielony przez 10^-6 w celu uzyskania końcowego wyniku w [nm].

Średnia wartość długości fali wynosi:

λ_śr = (λ₂+λ₃+λ₄+λ₅+λ₆+λ₇+λ₈)/7 = 555,38 [nm]

1. Obliczanie błędów pomiarów

• błąd pomiaru promienia krzywizny soczewki

gdzie

λ_Na - długość fali równa 589^. 10 ^-9 m

r_m, r_n przyjmowane odpowiednio wartości

n = 4

Δr = 0,04 mm

zatem






















Każdy z wyników został dodatkowo w trakcie obliczeń podzielony przez 10³ w celu uzyskania końcowego wyniku w [mm].

Średnia wartość błędy wynosi:

ΔR_śr = (ΔR₂+ΔR₃+ΔR₄+ΔR₅+ΔR₆+ΔR₇+ΔR₈)/7 = 151,69 [mm]

stąd

δ(ΔR) = (ΔR/R)*100% ≈ 32%

• błąd pomiaru długości fali monochromatycznej (filtr 1)

Mamy wzór

zatem


[nm]


[nm]


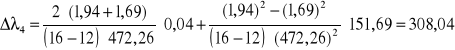
[nm]


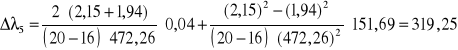
[nm]


[nm]


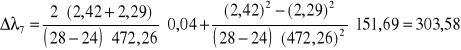
[nm]


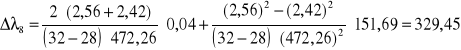
[nm]

Każdy z wyników został dodatkowo w trakcie obliczeń podzielony przez 10^-6 w celu uzyskania końcowego wyniku w [nm].

Wartość średnia błędu pomiarów wynosi:

Δλ_śr = (Δλ₂+Δλ₃+Δλ₄+Δλ₅+Δλ₆+Δλ₇+Δλ₈)/7 = 301,8[nm]

stąd

δ(Δλ) = (Δλ/λ)*100% = 71%

• błąd pomiaru długości fali monochromatycznej (filtr 2)

Ze wzoru jak wyżej obliczam


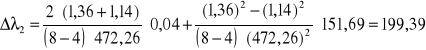
[nm]


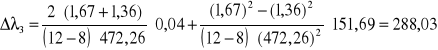
[nm]


[nm]


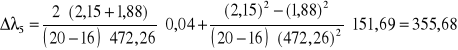
[nm]


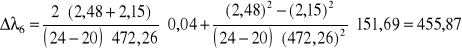
[nm]


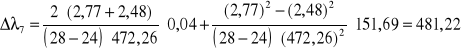
[nm]


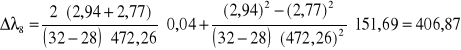
[nm]

Każdy z wyników został dodatkowo w trakcie obliczeń podzielony przez 10^-6 w celu uzyskania końcowego wyniku w [nm].

Wartość średnia wynosi:

၄ၬ_śr = (၄ၬ₂+၄ၬ₃+၄ၬ₄+၄ၬ₅+၄ၬ₆+၄ၬ₇+၄ၬ₈)/7 = 352,02 [nm]

stąd

ၤ(၄ၬ) = (၄ၬ/ၬ)*100% = 63%

5. Wnioski:

Na błędy pomiarów miały wpływ między innymi takie czynniki jak:

• niemożność dokładnego określenia środka pierścieni - kąt widzenia na to nie pozwalał,

• duża trudność w odróżnieniu pierścieni o rzędzie n > 20,

• duża czułość układu na wpływ czynników zewnętrznych takich jak szturchnięcia

• błędnego ustawienia mikroskopu (przesuniecie centralnego pierścienia w osi X)

Z poniższego zestawienia wyników można wywnioskować, iż pierwszy filtr był zbliżony do barwy pomarańczowej, której długość fali świetlnej wynosi


Natomiast drugi filtr był zbliżony do barwy niebieskiej, której długość fali wynosi


Filtr 1




























Filtr 2

























3

---