§5. Definicja liczb rzeczywistych. Moc zbioru: zbiory przeliczalne i nieprzeliczalne.

5.1 Zasada abstrakcji.

Relacje R nazywamy relacją równoważności jeżeli:

1. 
   xRx - zwrotność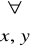

2. 
   xRy ⇒ yRx - symetria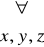

3. 
   (xRy ∧ yRz) ⇒ xRz - przechodność

Relacje równoważności oznaczamy symbolem „~”

Np. relacjami równoważności są :

Równość liczb rzeczywistych,

Równość zbiorów,

Równoległość prostych.

Zachodzi twierdzenie 1) zwane zasadą abstrakcji..

Jeżeli „~” jest relację równoważności wtedy elementami zbioru X ≠ ∅ oraz jeżeli każdemu elementowi x∈X przyporządkowuje zbiór A_x = { y∈X : x~y}, to:

1. 
   A_x ≠ Ø

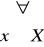
2. każdy element zbioru X należy do pewnego zbioru A_x

3. 
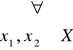
   [(A_x1 = A_x2) ∨ (A_x1 ∩ A_x2 = Ø)]

Dowód

Ponieważ relacja równoważności ~ jest zwrotna więc x ~ x, a stąd wynika, że x ∈ A_x.

Zatem zachodzi: a), b)

Dowodzimy c):

Przypuśćmy, że c) nie zachodzi tzn. dla pewnych elementów x₁, x₂ należących do X mamy (*) A_x1 ≠ A_x2 oraz A_x1 ∩ A_x2 ≠ Ø.

Czyli istnieje y należące do X takie, że y ∈ A_x1 ∩ A_x2.

Wykażemy, że A_x1 = A_x2.

Niech a ∈ A_x1 wtedy x₁ ~ a ⇒ a ~ x₁, otrzymujemy [(x₁ ~ y) ∧ (a ~ x₁)] ⇒ (a ~ y) ponad to x₂ ~ y ⇒ y ~ x₂, jest prawdziwe [(a ~ y) ∧ (y ~ x₂)] ⇒ (a ~ x₂) ⇒ (a₂ ~ a) czyli a ∈ A_x2. Zatem A_x1 ⊂ A_x2.

Analogicznie otrzymujemy A_x2 ⊂ A_x1 stąd A_x1 = A_x2 sprzeczność(*) dowodzi c).

Relacja równoważności ~ dzieli zbiór X ≠ Ø na pewną ilość podzbiorów niepustych i parami rozłącznych. Podzbiory te nazywamy klasami abstrakcji lub klasami równoważności.

Przykład.

Niech X oznacza zbiory wszystkich prostych na płaszczyźnie wtedy dla prostych p₁, p₂ ∈X relacja p₁ ~ p₂ ⇔ p₁ ║ p₂ jest relacją równoważności.

Natomiast klasy abstrakcji są to wtedy podzbiory prostych wzajemnie równoległych. Proste równoległe na płaszczyźnie wyznaczają kierunki na płaszczyźnie. Kierunkami na płaszczyźnie nazywamy kasy abstrakcji prostych równoległych na płaszczyźnie ze względu na relację równoległości.

Ciągiem nazywamy funkcją f określoną na zbiorze liczb naturalnych N.

Jeżeli F(n) = a_n dla n ∈ N, to funkcję f oznaczamy symbolem (a_n).

Wartości funkcji (a_n) dla kolejnych liczb naturalnych to jest elementy a_n nazywamy, n ∈ N wyrazami ciągu.

W przypadku ciągu (a_n) rozróżniamy zbiory wyrazów ciągu (a_n) oraz zbiór wartości ciągu (a_n0 jako funkcji.

Np.: ciąg ((-1)ⁿ⁺¹) ma zbiór wyrazów postaci:

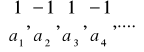
oraz dwuelementowy zbiór wartości {1, -1}

Definicja liczb rzeczywistych.

Zakładamy, że jest znana arytmetyka licz wymiernych.

Ciąg x = (w_n) o wyrazach będących liczbami wymiernymi nazywamy zbieżnym gdy dla każdej liczby wymiernej ε > 0 istnieje wskaźnik N > 0 taki, że dla wszystkich m, n > N zachodzi nierówność:

| w_n - w_m | < ε ,

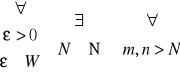
| w_n - w_m | < ε.

Niech X będzie zbiorem wszystkich zbieżnych ciągów liczb wymiernych. Dla x, y ∈ X gdzie x = (w_n), y = (v_n) określonych relację x ~ y ⇔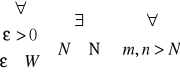
| w_n - v_n | < ε.

Relacja ta jest relacją, równoważności gdyż:

1. 
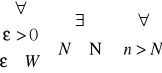
   | w_n - v_n | = |0| = 0 < ε czyli x ~ x,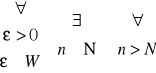

2. 
   | w_n - v_n | = | -( w_n - v_n )| = | v_n - w_n | < ε czyli x ~ y, to y ~ x

3. dla x = (w_n), y = (v_n), z = (u_n) ∈ X mamy x ~ y, y ~ z, x ~ z tzn.

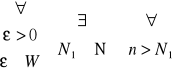
| w_n - v_n | <

oraz

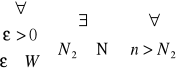
| v_n - u_n | <

zatem

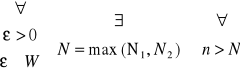
| w_n - v_n | = |( w_n - v_n ) = ( v_n - u_n )| ≤ | w_n - v_n | +

+| v_n - u_n | <
+
= ε czyli x ~ z

Klasy abstrakcji, na które dzielimy relacja ~ zbiór X wszystkich zbieżnych ciągów liczb wymiernych nazywamy liczbami rzeczywistymi.

Oznaczamy przez α, β, γ ... liczby rzeczywiste. Wtedy sumę α + β definiujemy następująco.

α + β = γ ⇔
x + y = z

przy czym równość x + y = z oznacza, że gdy x = (w_n), y = (v_n), z = (u_n) to

w_n + v_n = u_n

Suma α + β jest określona jednoznacznie, to znaczy nie zależy od tego, które ciągi x∈α, y∈β zostaną wybrane.

Iloczyn liczb rzeczywistych α, β określamy przyjmując:

α • β = γ
x • y = z

przy czym dla x = (w_n), y = (v_n), z = (u_n) zapis x • y = z oznacza, że:
w_n • v_n = u_n

Również iloczyn jest określony jednoznacznie. Nierówność ≤ w zbiorze liczb rzeczywistych określamy przyjmując dla liczb rzeczywistych α, β

α ≤ β ⇔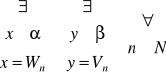
w_n ≤ v_n

α < β ⇔ (α ≤ β ∧ α ≠ β)

Liczbą rzeczywistą wymierną nazywamy liczbę rzeczywistą α taką, że {w}={w, w, w, w, ...} ∈ α, gdzie w jest liczb wymierną.

Istnieje wzajemnie jednoznaczne odwzorowanie f zbioru liczb wymiernych W na zbiór liczb rzeczywistych wymiernych, określonych przez funkcję.

α = f(w) ⇔ {w}∈ α

Można sprawdzić, że

f(w+v) = f(w) + f(v),

f(w•v) = f(w) • f(v)

w ≤ v ⇒ f(w) ≤ f(v)

Ponieważ odwzorowanie f zachowuje działania asymetryczne dodawania i mnożenia oraz relacje nierówności, więc można nie rozróżniać liczb wymiernych oraz liczb rzeczywistych wymiernych. Wtedy zbiór liczb rzeczywistych można uważać za rozszerzenie zbioru liczb wymiernych.

Powyższa definicja należy do G. Cantora.

Oprócz tej definicji znana jest również definicja liczb rzeczywistych przy pomocy przekrojów pochodzące do Ryszarda Dedekind'a oraz z aksjomatyczna definicja liczb rzeczywistych.

5.2 Równoliczność zbiorów.

Zbiory A oraz B nazywamy równolicznymi, lub równej mocy jeżeli jest określona funkcja odwzorowujące jeden z nich wzajemnie jednoznacznie na drugi. Piszemy wtedy A ~ B. Rownoliczność jest relacją równoważności. Relacja ta dzieli zbiory na klasy abstrakcji zbiorów równolicznych.

Klasy te nazywamy mocami zbiorów lub liczbami kardynalnymi. Moc zbioru oznaczamy symbolem
.

Przykłady:

1. Liczbą kardynalną wszystkich zbiorów, które mają n elementów jest liczba naturalna n

2. Zbiory liczb naturalnych N = {1, 2, 3, ...} jest równoliczny np. ze zbiorami:

1. zbiór liczb parzystych dodatnich

2. zbiór liczb nieparzystych dodatnich

3. zbiór liczb naturalnych postaci 3n = 2, n ∈ N

Gdyż istnieją funkcje wzajemnie jednoznaczne odwzorowujące zbiór n na jego podzbiory wymienione kolejno w a), b), c):

1. f(x) = 2x

2. f(x) = 2x - 1

3. f(x) = 8x + 2

3. Przedział
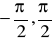
   , cała oś rzeczywista ±* są zbiorami równolicznymi, gdyż funkcja

f(x) = tgx dla x ∈ (
) odwzorowuje wzajemnie jednoznacznie (
) na

(-* , +* ).

Zachodzi twierdzenie 2 (Cantor - Bernstein)

Jeżeli zbiór A jest równy mocy z częścią zbioru B, a zbiór B jest równej mocy z częścią zbioru A to zbiory A oraz B są równej mocy.

Zbiór A nazywamy nieskończonym, jeżeli jest równej mocy z pewnym swoim podzbiorem właściwym B, tzn. A ⊃B, A ≠ B, B ≠ * wtedy
=
.

Zbiór A nazywamy skończonym, jeżeli A nie jest nieskończony.

5.3 Zbiory przeliczalne.

Zbiór nazywamy przeliczalnym, jeżeli jest skończony lub jest równej mocy ze zbiorem liczb naturalnych. Liczbę kardynalną zbioru liczb naturalnych oznaczamy literą alfabetu hebrajskiego „alef” z indeksem 0:

S₀

Przykład zbiorów przeliczalnych:

1. Zbiory liczb parzystych

2. Zbiory liczb nieparzystych

3. Zbiory liczb całkowitych

4. Zbiory liczb wymiernych

5. Zbiory liczb pierwszych tzn. maja tylko dwa dzielniki 1 i siebie.

Twierdzenie 3 (zasada indukcji zupełnej)

Niech każdej liczbie naturalnej n będzie przyporządkowane zdanie p(n).

Jeżeli:

1. Zdanie p(1) jest prawdziwe

2. Jeżeli p(n) jest zdaniem prawdziwym, to zdanie p(n+1) jest prawdziwe dla każdego n = 1, 2, 3,....

Dowód. Skorzystamy z następującej własności liczb naturalnych.

W każdym niepustym podzbiorze zbioru liczb naturalnych istnieje najmniejsza.

Przypuśćmy, że założenie a, b, są spełnione oraz, że istnieje liczba naturalna n, dla której p(n) nie zachodzi. Oznaczmy przez
zbiór tych liczb naturalnych n, dla których p(n) jest zdaniem fałszywym.

Zgodnie z zaprzeczeniem tezy zbiór A jest niepusty, a więc zawiera liczbę najmniejszą. Oznaczmy ją przez n₀. Z założenia a) wynika, że p(1) jest zdaniem prawdziwym a więc n₀=1 jest liczbą naturalną. Ponieważ n₀ jest najmniejszą liczbą w zbiorze A, więc n₀-1
A, czyli zdanie p(n₀-1) jest prawdziwe.

Z założenia b) wynika, że jest prawdziwe zdanie p(n₀), co jest sprzeczne z definicją n₀∈ A.

Ponieważ przypuszczenie, że istnieją liczby naturalne n, dla których p(n) nie zachodzi doprowadziło do sprzeczności, więc zdanie p(n) jest prawdziwe dla n = 1, 2, 3, ...

Wniosek

Jeżeli:

1. Zdanie p(n) jest prawdziwe dla liczby całkowitej n₀

2. Z prawdziwości p(n) dla liczby całkowitej k wynika prawdziwość p(n) dla k+1, gdzie

k ≥ n₀ to p(n) jest prawdziwe dla wszystkich liczb całkowitych n ≥ n₀.

Zbiory nieprzeliczalne.

Zbiór A, który nie jest przeliczalny, nazywamy nieprzeliczalnym.

Twierdzenie 4 : Zbiór liczb rzeczywistych jest nieprzeliczalnym. Zbiory równej mocy ze zbiorami liczb rzeczywistych nazywamy zbiorami mocy continuum, a ich liczbę kardynalną oznaczamy małą gotycką literą (c).

Np.: zbiór liczb rzeczywistych przedziału (a, b) gdzie b - a > 0 jest mocą continuum.

Rozdział II Przestrzenie metryczne.

Niepusty zbiór X nazywamy przestrzenią metryczną jeżeli określony jest funkcjonał (tzn. funkcja o wartościach liczbowych rzeczywistych lub zespolonych) zwany metryką.

„ro”

ρ : X × X →

Przy czym:

1. ρ (x, y) ⇔ x = y

2. ρ (x, y) = ρ (y, x)

3. ρ (x, y) ≤ ρ (x, z) + ρ (z, y) - warunek trójkąta dla dowolnych x, y, z ∈ X

Wtedy ρ (x, y) nazywamy odległością x od y. Przestrzeń metryczną oznaczamy symbolem

Przykład przestrzeni metrycznych:

1. Przestrzeń liczb rzeczywistych R z metryką ρ (x, y) = |x-y| : <R, II>

2. Przestrzeń liczb zespolonych C z metryką ρ (z₁, z₂) = | z₁, z₂| : <C, II>

3. Przestrzeń funkcji ciągłych na przedziale domkniętym <a, b> z metryką ρ (f, g) =

= max |f(x) - g(x)| : x ∈ <a, b> C (<a, b>).

* 1. Przestrzeń liczb rzeczywistych.

Przestrzeń liczb rzeczywistych <R, II> jest to zbiór R liczb rzeczywistych z metryką ρ (x, y) = |x - y| dla x, y ∈ R, gdyż:

1. |x - y| = 0 ⇔ x - y = ) ⇔ x = y

2. |x - y| = |-(x - y)| = |y - x|

3. |x - y| = |(x - z) + (z - y)| ≤ |x - z| + |z - y|

1.2 Kresy

niech E ⊂ R, E ≠ ∅

Zbiór E jest ograniczony z góry (z dołu), jeżeli:

Wtedy y nazywamy ograniczeniem góry (dolnym) zbiory E.

Jeżeli zbiór E jest ograniczony z góry oraz z dołu to nazywamy go zbiorem ograniczonym.

Np.: przedział <a, *) jest ograniczony z dołu, a przedział (-*, b> jest ograniczony z góry.

Przedział domknięty <a, b> jest ograniczony.

Definicja.

Niech zbiór E będzie ograniczony z góry. Mówimy, że liczba M jest kresem górnym (supremum) zbioru E jeżeli:

1. M jest ograniczeniem górnym zbioru E.

2. Jeżeli x < M to x nie jest ograniczeniem górnym. Piszemy wtedy M = supE

Definicja.

Nich zbiór E będzie ograniczony z dołu. Mówimy, że liczba m jest kresem dolnym (intimum) zbioru E jeżeli:

1. m jest ograniczeniem dolnym zbioru E

2. jeżeli x > m to x nie jest ograniczeniem dolnym zbioru E. Piszemy wtedy m = infE

Można napisać

M = supE *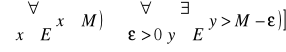

m = infE*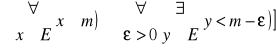

Przykład:

1. Niech E = { n: n = 1, 2, 3, ...} wtedy infE = 1. Zbiór E jest nieograniczony z góry.

2. Niech E = {-
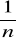
   : n = 1, 2, 3, ...} wtedy supE = 0 ∉E

infE = -1

Rzeczywiście obierzmy dowolne ε>0 wtedy supE = M = 0, gdyż dla każdego x∈ E mamy

x< 0 bo x = -

y = -
> M - ε = 0 - ε = - ε ⇔
< ε ⇔
< n czyli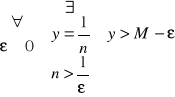

Twierdzenie 1

Jeżeli E jest niepustym zbiorem liczb rzeczywistych ograniczonym z góry (ograniczonym z dołu) to istnieje kres górny zbioru E ( kres dolny zbioru E).

1.2 Prosta rozszerzona

Rozszerzonym zbiorem liczby rzeczywistej nazywamy zbiór składający się z liczb rzeczywistych oraz z elementów oznaczanych symbolami: -*, +*, przy czym przyjmujemy:

1. Jeżeli x jest liczbą rzeczywistą to -*< x < +*

oraz

x + (+*) = +*

x + (-*) = -*

(+*) + (+*) = +*

(-*) + (-*) = -*

2. Jeżeli x > 0 to:

x • (-*) = -*

x • (+*) = +*

3. Jeżeli x < 0 to:

x • (-*) = +*

x • (+*) = -*

Rozszerzony zbiór liczb rzeczywistych oznaczamy symbolem:

Nich zbiór E ⊂

. Jeżeli zbiór E jest nieograniczony z góry, to znaczy dla
, to supremum zbioru E supE = +* kres dolny zbioru E ⊂
, który nie jest ograniczony z dołu, określamy następująco infE = -*.

W przestrzeni
wyróżniamy przedziały półdomknięte (półotwarte):

<a, b) = {x ∈
: a ≤ x < b}

(a, b> = {x ∈
: a < x ≤ b},

a także zbiory:

otoczenie punktu x₀ o promieniu r > 0

V_r (x₀) = (x₀ - r, x₀ + r)

Sąsiedztwo punktu x₀ o promieniu r >o

S (x₀) = V_r (x₀) \ {x₀}

Punkt x₀ ∈
nazywamy punktem skupienia zbioru E. E ⊂
, jeżeli każde otoczenie punktu x_o zawiera element zbioru E różny od x₀. Przykład:

Zbiór E = {
: n = 1, 2, 3, ...} ma punkt skupienia x_o = 0.

1

25

C = {±1, ±2, ±3, ...}

N +{1, 2, 3, ..}

R - zbiór liczb rzeczywistych

W = zbiory licz wymiernych

---